Статическая устойчивость механического движения
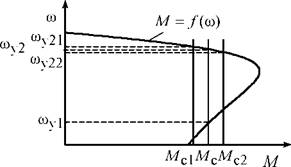
Установившийся режим работы электропривода вытекает из уравнения движения (2.1) при равенстве момента, развиваемого электрической машиной, и момента сопротивления на ее валу. При этом динамический момент будет равен нулю. В качестве примера определение установившегося значения скорости графически приведено на рис. 2.1. Однако для более сложной механической характеристики асинхронного двигателя могут существовать две точки со^ и со v,2, определяющие равенство момента движения М и момента сопротивления Мс (рис. 2.7).
|
Рис. 2.7. Определение статической устойчивости механического движения |
Рассмотрим работу электропривода в точке установившегося вращения со^. Как уже отмечалось ранее, в электроприводе практически
всегда возникают проблемы при соединении электрической машины и нагрузки. Основные трудности возникают из-за несоосности и эксцентриситета вращающихся валов. В этом случае нагрузка на валу двигателя все время изменяется. При ее незначительном увеличении, например, до значения Мс2, в соответствии с уравнением движения М - Мс2 = Мдин, динамический момент Мдин уменьшится, а это в
свою очередь приведет к уменьшению скорости двигателя. В соответствие с механической характеристикой двигателя его момент также уменьшится, динамический момент Мдин уменьшится вновь, что в конечном итоге приведет к полной остановке электропривода.
При уменьшении момента сопротивления на валу двигателя, например до значения Мс1, динамический момент Мдин увеличится, что
в соответствии с уравнением движения приведет к увеличению скорости двигателя. Момент двигателя возрастет, возникнет дополнительный ускоряющий динамический момент, который заставит электропривод разогнаться до новой установившейся скорости соу22 •
Рассмотрим работу электропривода в точке установившегося вращения соу2. Если по какой-либо причине нагрузка на валу двигателя
возрастет, например, до значения Мс2, то в соответствии с уравнением движения М - Мс2 = Мдин динамический момент Мдин уменьшится, что приведет к торможению электропривода. Новая точка установившейся работы С0у22 будет определяться равенством момента движения и
момента сопротивления на валу двигателя, то есть при М = Мс2.
Аналогично ведет себя электропривод при уменьшении момента сопротивления на валу двигателя - он перейдет в новую точку установившегося вращения C0y2i.
В общем случае условие статической устойчивости электропривода в окрестностях некоторой точки со у определяется неравенством:
£р - £рс < 0, (2.12)
dMc АМс
где кпс =-------- -«------- - статическая жесткость механической характе
р/со Доо
ристики производственного механизма, приведенная к валу двигателя.
Статическая устойчивость электропривода при известных аналитических уравнениях механических характеристик электродвигателя и производственного механизма легко определяется по выражению (2.12) путем численного дифференцирования характеристик по скорости со.