ЭЛЕКТРИЧЕСКИЙ ПРИВОД

Приведение моментов инерции к одной оси вращения

Для упрощения расчета переходных процессов электропривод, об­ладающий распределенными моментами инерции J >

JM2,Jp0 (см. рис. 2.8), сводят к одномассовой системе с эквивалентным моментом инерции • Эквивалентная одномассовая система электро­привода (рис. 2.9), имеющая момент инерции, вращается со скоро­стью электродвигателя со.

Приведение моментов инерции к одной оси вращения производит­ся на основании принципа сохранения кинетической энергии исходной многомассовой системы с распределенными моментами инерции и од­номассовой системы с эквивалентным моментом Схема включения и статические характеристики двигателя постоянного тока независимого возбуждения

Двигатели постоянного тока выполняют с дополнительными полюсами с целью улучшения процессов коммутации. Компенсационная обмотка в машинах постоянного тока обеспечивает компенсацию поперечной составляющей реакции якоря.

Дополнительные обозначения, принятые на рис. 3.1:

М - обмотка якоря двигателя;

LM - обмотка возбуждения;

U - напряжение обмотки якоря, В;

I - ток обмотки якоря, А;

Е - ЭДС обмотки якоря, В;

Доя - активное сопротивление обмотки якоря, Ом;

- добавочное сопротивление цепи обмотки якоря, Ом;

U0B - напряжение обмотки возбуждения, В.

Вывод уравнений статических характеристик двигателя постоянно­го тока проведем с учетом следующих допущений:

• щетки якоря стоят на геометрической нейтрале, поэтому попе­речную реакцию якоря не учитываем и считаем поток, созданный об­моткой возбуждения, постоянным;

• потерями в подшипниках, щеточно-коллекторном узле и на вентиляцию пренебрегаем, то есть считаем момент на валу двигателя равным электромагнитному моменту.

Запишем уравнение по второму закону Кирхгофа для якорной цепи электродвигателя:

U = Е +1 Rm, (3.1)

где Дяц = Ддв + Яд - полное сопротивление цепи обмотки якоря; ^дв = ^оя + ^дП + 1?ко ~ сопротивление двигателя, равное сумме сопро­тивлений обмотки якоря, дополнительных полюсов и компенсационной обмотки.

ЭДС обмотки якоря можно найти в соответствие с уравнением Максвелла:

Е = к - Ф-ю, (3.2)

где Ф - магнитный поток, созданный обмоткой возбуждения, Вб; со - угловая скорость двигателя, рад/с; к = zp ■ N/(2 ■ п ■ а) - конструктив­ный коэффициент двигателя постоянного тока; zp - число пар полюсов

двигателя; N - число витков обмотки якоря; а - число параллельных ветвей обмотки якоря.

Подставив (3.2) в (3.1) и решив полученное выражение относитель­но угловой скорости со, получим уравнение электромеханической ха­рактеристики двигателя постоянного тока:

ю = (3.3)

к-Ф к-Ф

В соответствие с (3.3), электромеханической характеристикой двигателя постоянного тока называют зависимость его угловой скоро­сти со от тока якоря двигателя I.

Электромагнитный момент двигателя находится из уравнения Фа­радея:

М=к-Ф-1. (3.4)

Решим это равенство относительно тока якоря двигателя I и под­

ставим его в (3.3), получим уравнение механической характеристики двигателя постоянного тока:

<й = ——U йяц,. (3.5)

к-Ф (к-Ф)2

Механической характеристикой двигателя постоянного тока назы­вают зависимость его угловой скорости со от момента двигателя М.

Различают естественную и искусственные механические характе­ристики двигателя постоянного тока.

Естественной механической характеристикой двигателя постоян­ного тока называют зависимость угловой скорости двигателя со от мо­мента его М, полученную при номинальной схеме включения двигате­ля, номинальных параметрах напряжения обмоток якоря и возбуждения и отсутствии добавочных сопротивлений в цепях двигателя. Все ос­тальные характеристики называют искусственными. С помощью ис­кусственных характеристик производят регулирование скорости двига­теля. Как следует из уравнений (3.3) и (3.5), регулировать скорость дви­гателя постоянного тока независимого возбуждения можно тремя ос­новными способами:

• изменением добавочного активного сопротивления R в цепи обмотки якоря двигателя;

• изменением подводимого к обмотке якоря напряжения U;

• изменением потока возбуждения двигателя Ф,

а также изменением различных комбинаций этих параметров.

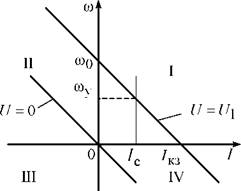
Выражения (3.3) и (3.5) при неизменных параметрах R, U, Ф представляют собой уравнения прямой линии. В качестве примера на рис. 3.2. приведены электромеханические характеристики двигателя по­стоянного тока независимого возбуждения, построенные в четырех квадрантах.

Как уже отмечалось, в первом квадранте электрическая машина по­стоянного тока независимого возбуждения работает в двигательном ре­жиме, преобразуя электрическую энергию в механическую. Двигатель­ный режим работы ограничен двумя характерными точками:

1. Первая координата точки определяется при токе якоря, равном нулю, вторая координата получается из уравнения (3.3) при подстанов­ки в него 1 = 0. Скорость двигателя, соответствующая нулевому току якоря, называется скоростью идеального холостого хода:

U ™

Щ=—-• (3.6)

к-Ф

В режиме идеального холостого хода двигатель не получает пита­ния по цепи обмотки якоря из питающей сети.

2. Первая координата второй точки соответствует скорости двига­

теля, равной нулю. При подстановке в (3.3) со = 0 получим ток якоря двигателя короткого замыкания

(З-7)

“яц

Мощность двигателя равняется нулю, так как его скорость со = 0, а вся получаемая из сети энергия расходуется на нагрев сопротивлений якорной цепи двигателя і? яц = і? дв + R.

Генераторный режим работы электрической машины независи­мого возбуждения параллельно с сетью или режим рекуперативного торможения возникает, если скорость вращения машины превышает скорость идеального холостого хода со0. Электрическая машина работа­ет во втором квадранте. При этом ЭДС машины Е становится больше напряжения обмотки якоря U и в соответствии с выражением (3.1) ток якоря меняет знак, становясь отрицательным:

IT - F

/ = (3-8)

'Чгц

При работе электрической машины генератором параллельно с се­тью она получает механическую энергию от рабочего органа исполни­тельного механизма и преобразует ее в электрическую. Необходимо помнить, что электрическая энергия, возвращаемая в цепь источника напряжения обмотки якоря, должна потребляться параллельно вклю­ченной якорю нагрузкой.

При работе электрической машины в четвертом квадранте наступа­ет режим торможения противовключением или генераторный режим работы последовательно с сетью. В этом генераторном режиме энер­гия в сеть, питающую обмотку якоря, не отдается. Скорость вращения электрической машины меняется на противоположную двигательному режиму работы, то есть при данной схеме включения - становится от­рицательной. Режим работы возникает при преобразовании потенпио- нальной энергии в электрическую (активная нагрузка на валу двигателя) или при преобразовании кинетической энергии в электрическую (тор­можение двигателя при смене полярности напряжения на обмотке якоря на противоположную). Во всех случаях ЭДС якоря электрической ма­шины будет иметь тот же знак, что и напряжение обмотки якоря. Ток, протекающий по обмотке якоря, определяется уравнением

1=и^-т=и±Е

U U v 7

яц яц

Электрическая энергия от протекающего по якорю тока рассеива­ется на активных сопротивлениях якорной цепи двигателя і? яц = ^дв + ^д, преобразуясь в тепловую. Энергетически режим тормо­жения противовключением самый неблагоприятный из всех режимов работы электрической машины независимого возбуждения.

На рис. 3.2 приведена электромеханическая характеристика, про­ходящая через начало координат. Такой режим работы электрической машины возможен при ее отключении от источника напряжения якоря (U = 0), а для возможности протекания тока якоря - при замыкании че­рез добавочное сопротивление накоротко. В этом случае режим работы электрической машины постоянного тока независимого возбуждения называется динамическим торможением. Схема включения электриче­ской машины в режиме динамического торможения приведена на рис. 3.3.

Уравнение электромеханической характеристики образуется из вы­ражения (3.3) при подстановке в него напряжения якоря U = 0:

R„ тт

ю = -/—5і-. (3.10)

к ■ Ф

Ток в якоре электрической машины протекает за счет ЭДС Е = к • Ф • со:

1 = J~. (3.11)

“яц

Режим работы возникает при преобразовании потенциональной энергии в электрическую (активная нагрузка на валу двигателя) или при преобразовании кинетической энергии в электрическую (торможение двигателя при уменьшении напряжения на обмотке якоря до нуля). Электрическая энергия от протекающего по якорю тока также рассеива­ется на активных сопротивлениях якорной цепи двигателя і? яц = ^дв + , преобразуясь в тепловую.