ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Вытеснение нефти растворами активных примесей
Понятие активной примеси. Основные уравнения. Рассмотрим двухфазное фильтрационное течение нефти и воды, предполагая, что вода (а возможно, и нефть) содержит некоторую добавку, способную влиять на гидродинамику потока. Такую добавку независимо от ее природы назовем активнойпри - м е с ь ю. Концентрацию примеси будем считать малой и не меняющей удельных объемов фаз. К активным примесям можно отнес - ти практически все химические реагенты, применяемые для увеличения нефтеотдачи. При всем разнообразии механизмов их действия гидродинамическое описание роли таких примесей оказывается в сделанном предположении единым. Действительно, поскольку в силу независимости плотности фаз от содержания примеси уравнения баланса воды и нефти не изменяются, любое гидродинамическое действие активной примеси может сводиться лишь к изменению проницаемости k, фазовых проницаемостей вязкостей ці и капиллярного давления Рс. В свою очередь, это сводится, в силу сказанного в гл. IV, к влиянию активной примеси на проницаемость k (что существенно лишь при описании неодномерных процессов), на функцию распределения потоков F и на функцию Рс (что, в свою очередь, существенно в тех условиях, когда капиллярным скачком давления нельзя пренебречь). Таким образом, при описании одномерных крупномасштабных процессов достаточно знать лишь влияние активной примеси на функцию распределения потоков F. Отдельным важным вопросом становится влияние примеси на неравновесные процессы. Этот вопрос должен стать предметом специального рассмотрения; в настоящее время по нему имеются лишь первоначальные представления.
Примесь может находиться в трех состояниях — растворенном в воде, растворенном в нефти и сорбированном пористой средой. Поэтому полное количество ее в единице объема среды равно (msci + + т( 1—s)c2 + a), а поток CiUi + с2и2 + q, где с,- — концентрация примеси в і-й фазе; а — количество примеси, сорбированное пористым скелетом; q — диффузионный поток. Уравнение баланса примеси имеет вид
[msci +m(l—s)c2+a]ll+ div (^и, + c2u2 + q) = r, (V.44)
Где г — скорость генерации примеси в единице объема среды. Рассматривая крупномасштабные медленные процессы, следует пренебречь диффузионными потоками (см. § 1 данной главы), а распределение примеси между фазами считать термодинамически равновесным. Ограничимся в последующем рассмотрением одномерных движений. Тогда (при г = 0) имеем
Сі — с, с2 = ?(с), a = a(c, s), F = F (s, с), (V.45)
[msc + tn(\—s)<?{c)+a (с, s)], t + U [cF + f (с) (1 —F)], x = 0. (V.46)
Таким образом, задача о фронтальном вытеснении нефти раствором активной примеси в крупномасштабном (внешнем) приближении описывается системой уравнений (IV.33) и (V.46), содержащей три функции F (s, с), f (с), а (с, s), которые считаются заданными. Индивидуальность процесса проявляется лишь в конкретном виде этих функций.
Этот вывод при всей его простоте имеет принципиальное значение. Он определяет тот минимально необходимый объем эмпирической информации, который должен определяться до проведения расчетов. Полученная система уравнений позволяет описать такие основные процессы повышения нефтеотдачи, как вытеснение нефти растворами водорастворимых поверхностно-активных веществ, водорастворимыми полимерами и карбонизированной водой. Далее анализ проводится в самых общих предположениях о виде входных функций F(s, с), <р (с), а (с, s). Его результаты оказываются неожиданно простыми; они позволяют дополнительно ограничить требуемый объем исходной информации.
Фронтальное вытеснение нефти раствором активной примеси.
Автомодельные решения. Структура зоны вытеснения. Рассмотрим одномерное фронтальное вытеснение нефти из полубесконечного пласта раствором активной примеси. При сделанных предположениях задача сводится к решению системы уравнений:
Ms, t + U [F (s, с)]., = О, [mcs + т? (с) (1 — s) + а] , + U [cF + (1 - F) 7 (с)]. * = О, (V.47) 0</< оо, 0<л;< оо, U> О при начальных и граничных условиях
S(x, 0) = so, с(х, 0) = со, s(0, t) = s°, с(0, t) = с0. (V.48)
Возникшая ситуация близка к той, которая хорошо изучена в газовой динамике. Эта аналогия существенно облегчает исследование.
Анализ размерностей показывает, что решение этой задачи автомодельно и имеет вид
S = s(5); с = с(Е); l = mx/Ut, (V.49)
Где s (?), с (£) удовлетворяют системе обыкновенных дифференциальных уравнений
£ ds __ dF (s, с)
4Si" dt ' (V.50)
,dfcs + (l— s)y (c) + g/ml _ d [cF + у (с) (1 - F)}
5 ds Ті
При краевых условиях
S(0) = s°, c(0) = c°, s(oo) = S0, с(оо) = с0. (V.51)
При этом, как и в газовой динамике, ни исходная задача (V.47) — (V.48) для уравнений в частных производных, ни задача (V.50) — (V.51) для системы обыкновенных дифференциальных уравнений не имеют, вообще говоря, классического решения, и необходимо допустить существование решений со скачками. На скачка х должны выполняться соотношения баланса массы фаз и примеси, сводящиеся к условиям
MV [s+ — s-] = U [F (s+, c+) — F (s~, с-)], (V.52)
L — с— н - ср (с—) — ?(с+) J
= U [F+ + (у.53)
Здесь V — скорость скачка; s~, с~, s+, с+ — соответственно значения за скачком и до него. Скачки могут быть либо скачками насыщенности при неизменной концентрации — тогда существенно лишь условие (V.52), a (V.53) выполняется тождественно, либо сопряженными скачками концентрации и насыщенности.
Соответственно этому могут существовать скачки и в автомодельном решении, и условия на них получаются из общих условий заменой mV/U на £/, где — значение автомодельной переменной, соответствующее скачку.
При этом оказывается, что можно построить бесконечно много решений, удовлетворяющих уравнениям, начальным условиям и условиям на скачках. Физически осмысленное решение должно удовлетворять дополнительному условию устойчивости скачков. Каждый из них характеризуется пятью величинами — значениями скорости скачка V и значениями искомых величин перед (s+, с+) и за скачком (s_, с~). Эти пять величин связаны двумя условиями: (из двух условий (V.53) одно является следствием другого и условия (V.52)). Для того, чтобы устранить неопределенность, т. е. обеспечить устойчивость скачка, необходимы еще три дополнительных соотношения, которые прямо или косвенно отражают влияние начальных и граничных условий задачи. Это влияние передается вдоль характеристик исходной системы дифференциальных уравнений; каждая приходящая в данную точку характеристика дает одно соотношение меж^у переменными (для системы (V.47) характеристики и соотношения на них выписаны ниже). В данном случае для устойчивости скачка необходимо, чтобы на него приходили три характеристики. В общем случае системы п уравнений сохранения типа (V.47) для переменных с п соотношениями на скачках для устойчивости скачка необходимо, чтобы на него приходила (п - f 1) характеристика. Это услоЕие устойчиЕости скачка используется в ряде задач теории ударных еолн; строгое его доказательство известно для одного уравнения типа первого (V-47) и системы квазилинейных гиперболических уравнений, однако при условиях, которым системы рассматриваемого нами типа не удовлетворяют. Поэтому в дальнейшем это условие используется как эвристическое. Некоторым обоснованием этих условий служит анализ тонкой структуры скачков (см. § 3 гл. V). Приходящими на скачок из зоны за скачком будут при этом считаться характеристики, скорость которых не меньше скорости скачка; из зоны перед скачком — характеристики, скорость которых не больше скорости скачка. Иными словами, любая характеристика, имеющая равную со скачком скорость, считается приходящей на скачок [36]; характеристики, не удовлетворяющие этому условию, считаются ух од ящими.
Для системы (V.47), как легко убедиться, характеристики определяются соотношениями
Dx\ U dF (s, с) ds Гг, F + <р' (с) (1 — F)
Dt[F
+
Dt т ds ' dt [ • s s + (1 — s) 9' (c) + a'/m + F dc -Q - dx2. U F + y'(c)(l-f) . dc "
^ •cdt dt m s-\-(l—s)?'(c) + a'(c)/m ' dt ~
Допустим, что задача решена. Тогда, зная функции s(Ј) ис(£), можно для каждого £ вычислить F (s, с), а затем, исключая из указанных зависимостей £ и с, получить связь между F и s, поэтому каждому £ отвечает некоторая точка на плоскости s, F в квадрате (0,1) х (0,1), а всему решению — кривая, которую в дальнейшем мы будем называть путем. Поскольку в силу первого уравнения (V.50) X = dF/ds, где производная берется вдоль пути (s, F), автомодельное решение однозначно восстанавливается, если он задан. При этом скачкам решения соответствуют прямолинейные участки пути, а угловым точкам — участки постоянства насыщенности; концентрация с на непрерывных участках решения неявно задана соотношением F = F (s, с).
Решающую роль играет то обстоятельство, что путь на (s, F) — диаграмме удается построить, причем зачастую вполне элементарными средствами, до решения задачи. Особенно просто осуществляется построение в случае, если скачок концентрации распространяется без размазывания, т. е. существует подлежащее отысканию значение Хс такое, что
С = с°, 0 < S < Хс, с = со, Ъ < « < °о (V.55)
(достаточные условия распространения скачков концентрации без размазывания указаны ниже).
Используя уравнения (V.50), условия (V.52) и (V.53), и условие устойчивости скачков, можно дать элементарную графическую технику построения пути (s, F) и, следовательно, решения, обобщающую известный способ решения задачи Баклея—Леверетта, изложенный в гл. IV. В построении используются лишь кривые функции F(s, с) при двух значениях: с — начальном и конечном — и значения функций <f и а, отвечающие этим двум значениям концентрации активной примеси. Это обстоятельство весьма важно, поскольку дополнительно резко ограничивает требуемый объем экспериментов для получения исходных данных к расчетам. Очевидно, решение состоит из (примыкающего ко входу пласта, 0 < £ < £/) участка с с — с0, удаленного участка £ > £/, в котором концентрация примеси сохраняет первоначальное значение, с = Со, и скачка при £ = = £/, на котором изменяются и концентрация, и насыщенность. Первому участку на (s, F)—диаграмме отвечает отрезок кривой F(s, с0), второму — отрезок кривой F (s, Со). Из условий (V.52) следует, что относительная скорость скачка = mV/U равна угловому коэффициенту отрезка, соединяющего точки s+, F+ и s~, F~, отвечающие значениям переменных по обе стороны скачка (т. е. точно так же, как и в обычной теории Баклея —Леверетта, только соответствующие точки не обязательно располагаются на кривой F(s, с), отвечающей фиксированному значению концентрации примеси). Из условия (V.53) следует, что для скачка, происходящего с изменением концентрации, относительная скорость равна угловому коэффициенту прямой, соединяющей точки S+, F+ или s-, F~ с «полюсом» —sp, —Fp,
|
Примеси « FР = ДГ^ = - Х~У - А = (у-56) |
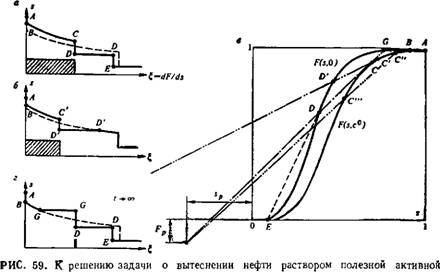
Таким образом, точки s+, F+, s~, F~ и —sp, —Fp лежат на одной прямой, и луч, отвечающий скачку, принадлежит пучку, проходящему через полюс (-—Sp, —Fp). Чтобы выбрать из этого пучка единственный «нужный» луч, заметим, что им не может быть луч, пересекающий кривую F (s, с0) «сверху» (рис. 59, в), так как при этом вблизи точки пересечения значение автомодельной переменной за скачком больше, чем на самом скачке:
S - = (dF (s, c°)/ds)~ > і, = (F~ - F+)/(s~ - s+), (V.57)
И «решение» получается неоднозначным. Если мы допустим, что луч, соответствующий скачку, пересекает кривую F (s, с0) «снизу» (см. рис. 59, в), то в точке сопряжения
Ї - - (dF/ds)~ < 6,. (V.58)
При этом число характеристик, приходящих на разрыв, равно лишь двум, и нарушается условие устойчивости скачка (см. подробнее ниже). Таким образом, путь на плоскости (s, F), отвечающий автомодельному решению, обязательно содержит скачок по лучу, проходящему через полюс (—sp, —Fp) и касающемуся кривой F (s, с0) в точке (s~, с) (см. рис. 59). (Здесь считается, что, как это обычно бывает, такая точка касания единственна. Можно показать, что из нескольких точек касания при построении решения нужно выбрать верхнюю.) После определения положения сопряженного скачка концентрации и насыщенности («с-переход»), дальнейшее достраивание решений в областях двухфазного потока с постоянной концентрацией примеси производится очевидным образом
По аналогии с теорией Баклея — Леверетта; два различных варианта возможных путей в (s, F) плоскости показаны на рис. 59.
На рис. 59 показаны соответствующие распределения насыщен - ностей в один момент времени для вытеснения водой (пунктир) и раствором активной примеси при малой (а) и значительной (б) сорбциях. Во всех случаях фронту примеси предшествует фронт вытеснения нефти водой; если сорбция значительна, он движется с той же скоростью, что и при вытеснении чистой водой. Это означает, что сильно сорбирующаяся примесь не изменяет момента обводнения и начальной стадии водного периода разработки; роль примеси при этом сводится к некоторому замедлению роста обводненности продукции на промежуточной стадии и увеличению полноты вытеснения нефти на заключительной стадии. Если примесь сорбируется слабо (а), то несколько затягивается безводный период эксплуатации и снижается обводненность продукции на начальной стадии обводнения.
Сходное построение позволяет проанализировать и применение активной примеси для довытеснения нефти из залежи, первоначально разработанной при заводнении (т. е. в качестве «третичного» метода). Построение соответствующего (s, F) пути показано на рис. 60, в, а характерные распределения насыщенностей по длине пласта — на рис. 60, а, б. Принципиально возможно образование двух типов решений. Один из них характеризуется отставанием фронта примеси от фронта вытеснения и образованием отчетливо выраженного нефтяного вала. Для решения второго типа характерно образование нефтяного плато с медленным снижением нефте - насыщенности на заднем его фронте; передний фронт плато совпадает с фронтом продвижения активной примеси (см. рис. 60, б). Какой именно из режимов осуществляется, можно определить на (s, F)- диаграмме. Если верхняя точка пересечения касательной к F (s, с0)
|
|
|
F |
|
В л |
|
РИС. 61. К решению задачи о вытеснении нефти раствором вредной активной примеси |
|
В |
|
І |
|
А |
|
|
|
В |
|
В |
|
У |
Из точки (—sp, —Fp) с F (s, Со) лежит на участке s > s0, то образуется нефтяной вал, в противном случае — нефтяное плато.
До сих пор речь шла о примеси, снижающей долю воды в во - донефтяном потоке, т. е. снижающей относительную подвижность воды или увеличивающей относительную подвижность нефти. Ясно, что полезные активные примеси принадлежат именно к этому классу. Можно, однако, поставить вопрос о роли примесей, увеличивающих относительную подвижность воды. Соответствующая задача вытеснения легко решается построением рис. 61, б и приводит к распределению насыщенности, показанному на рис. 61, а. Наличие примеси не влияет на структуру передней части зоны вытеснения; прохождение фронта примеси, отстающего от фронта закачиваемой воды, сопровождается некоторым увеличением водонасыщенности и доли воды в потоке, которые затем длительно сохраняются на постоянном уровне.
Рассмотрим построение автомодельного решения в общем случае, когда не предполагается, что существует полный скачок концентрации примеси, хотя и считается по-прежнему что содержание примеси в нефти и в пористом скелете зависит только от концентрации ее в воде (<р = ср(с), а —а (с)). В анализе нуждается только та часть решения (или соответствующего пути на s, F-диаграмме), на которой изменяется концентрация. Изменение концентрации может происходить в с-с к а ч к а х или с-в о л н а х (участках непрерывного изменения с (£)). Будем характеризовать с-скачки значениями концентрации по обе стороны скачка [с~, с+], причем с± = с (£/ ± 0); для определенности далее полагается с0 > cq.
Тогда возможны скачки четырех основных типов:
1) [с°, с0]; 2)[с°, с*]; с0 < с* < с0; 3) [с*, с,], со < с„ < с* < с0; 4) [с*, с0]; с0 < с* < с0.
Запишем соотношения на скачках в виде
= F--F+ _ f± + (Ay/Ac)(l-Ay/Acr' 5д>
1 s - — s+ ' s± +(Д<р/Дс+ ДЛ/Дс) (1 — Дср/Дс)-1
Здесь F± — F(s±, с±); каждое из уравнений (V.59) является следствием двух остальных. Обозначим через Хи2 безразмерные характеристики скорости по обе стороны скачка:
^ЛДЛ с±).
Из условия устойчивости скачка либо
Min ZT.2 < £/ < min Si;2, і,- < max (V.61)
Либо
Шах lft2 < Ij < max Е/ < min (V.62)
Заметим, что, если к скачку примыкают участки непрерывного изменения переменных (s - или с-волны), то из условия однозначности решения предельные значения автомодельной переменной в них удовлетворяют неравенству
< И,- < ;+. (V.63)
Учитывая, что на с - и s-волнах значение автомодельной переменной совпадает с характеристической скоростью, из (V.62) и (V.63) находим, что реализуется одно из следующих соотношений:
= max «fa > Г" = min XV.2 = Е/, V = min 17,2 = = min = Г = max ЕГг = max Xt.2 = = 6/, (V.64)
Г" = min S172 < = max Xt,2 = £/ < max ХГ.2-
Анализируя расположение характеристик обоих семейств, не трудно прийти к заключению, что для типичного расположения кривых F (s, с), показанного на рис. 59, (с0 — co)Ft е<0, при обычных значениях so и s° решение может содержать лишь скачки, для которых верны первые два соотношения (V.64). Рассмотрим вначале скачок типа [с0, с*]. Для него, очевидно, верно второе условие (V.64). Тогда в дополнение к уравнениям (V.59) имеем:
ГУл/1;) М = ^ is, Л (V.65)
Из (V.65) и (V.59) находим систему уравнений для определения с+ — с*, s+, s~, Xj. Ограничимся пока вариантами, когда эта система уравнений решается элементарными средствами. Пусть
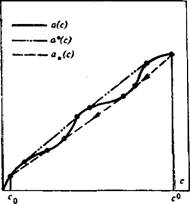
РИС. 62. К определению структуры решения по виду изотермы сорбции
Тогда из (V.65) и (V.59) имеем для с+ уравнения f+ + <Po/0-?o) f+ + ?o/0-*o)
(fo + ЛЛ/Дс)/(' - fo) s+ + Ы + ^ И]/(1 -<Ро)'
Откуда
А' (с+) = [а+ - а (с°)]/(с+ - с0), (V.67)
А с+ определяется как точка касания кривой а (с) касательной, проведенной из точки (с0, а (с0)) (рис. 62). После нахождения с+ с помощью следующего из (V.59) и (V.65) уравнения
|
|
|
С + |
|
Со |
|
С. с» с» |
F (s - со)= + _____________ (V.68)
Определяется s~ как абсцисса общей точки кривой F (s, с0) и касательной, проведенной к ней из точки (—Sp, —Fp),
W - (V-69)
(см. рис. 59). По угловому коэффициенту этой касательной определяется а по точке ее пересечения с кривой F(s, с*) — значение s+. Наконец, в области \ > имеем участок непрерывного изменения концентрации (с-волну).
Пусть решение содержит скачок третьего типа [с*, с,]. Из соотношений (V.59) и условий (V.64) получаем
T _ F± + Ау/(Ас — А?)
|
1 |
|
(V.70) |
_ s± + (Д9 + АЛ) /(Ас — Дер) ~ 52 —
F±+(p'±(l_,p'±)-
S± +(?'± + Л'±)(1-?'±)-
Если f = voc, по соотношениям (V.70) получаем
А' (с+) = а' (с-) = [а (с+) — а (с~)]/(с+ — с~). (V.71)
С+ и с~ — абсциссы точек кривой а (с), имеющих общую касательную (см. рис. 62); Е/ определяется как характеристическая скорость в с-волне, приходящей в точку (s~, F (s~, с~); значение s+ определяется как абсцисса точки М+ пересечения прямой, проведенной через точку М~ с угловым коэффициентом?/; с кривой F(s+, с+). Последующая с-волна строится из точки М+ в соответствии с уравнением
DF F + >/ (1 — у')-' (V 72)
Ds s + (4' + A')/(i-4') ■ 1 ■ '
Наконец, для скачка четвертого типа имеем с+ = с0;
F± + Д<р (Ac-A?)"1 + ? 1/(1-?1)
«/ = + ■ ,«. і A„wa.----- = «2 =
+ (Лг + АА)(Лс-Лг)~1 s-+ (у1 +»!)/(1-ТІ)'
(V.73)
|
А(с.) — а (сЛ С[ с2 А ("с,") — а (сЛ |
|
(V.74) |
В частности, при линейной функции 9 (с) значение с~ находится как общая точка кривой а (с) с касательной, проведенной к ней из точки Со, а (с0) (см. рис. 62). Таким образом, в рассматриваемом случае вся структура с-перехода определяется видом изотермы сорб - ции а (с). Рассмотримфункциюа (с) на отрезке Д [с0, с0] и построим на нем выпуклую и вогнутую оболочки а (с): а* (с) и а* (с)—минимальную невогнутую функцию, значения которой не меньше а (с), и максимальную невыпуклую функцию, значение которой не боль - шэ а (с):
2* (с) = шах
Си 4
Z* (с) = min
Сі, Є 4
График функции а# (с) состоит из выпуклых дуг, общих с графиком а (с), и прямолинейных участков. Прямолинейные участки отвечают с-скачкам; дуги — с-волнам. Построение решения сводится к последовательному (начиная с малых Е) построению пути на (s, F) диаграмме; при этом с-скачки находятся при помощи элементарного графического построения, а с-волны — численным интегрированием.
Аналогичная процедура построения решения проходит при с0 < со, F, с > 0; структура с-перехода при этом определяется видом функции а* (с).
Столь же просто устанавливается заранее структура с-перехода при произвольной функции <р (с), если й(с)зО. При этом необхо - д имо, чтобы
Д<р/Дс = <р'(с±). (V.75>
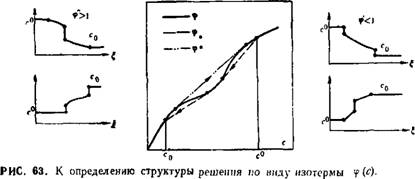
Здесь знак -+- берется для скачков второго типа, знак —- для скачков четвертого типа; для скачков третьего типа берутся уравнения с обоими знаками. Таким образом, при а(с) = 0 структура решения определяется видом вспомогательных функций <р* (с) и (с) (рис. 63) при со > с0 и с0 > с0 соответственно, при этом предполагается, что функции F (s, с) имеют обычный вид
Max [F (s, с) — s] > 0 > min [F (s, с) — s|.
S s
Если F, с (c° — со) > 0, то проходит аналогичная техника нахождения автомодельных решений (см. рис. 59), с той лишь разницей, что в этом случае построение следует начинать с больших значений Е и пользоваться соотношениями (V.64).
Изложенная процедура гарантирует построение одного автомодельного решения с устойчивыми скачками, но не гарантирует отсутствие других устойчивых решений.
|
І I |
|
|
Рассмотрим кратко возможности построения автомодельного решения в общем случае, когда? (с) — произвольная возрастающая функция, а количество сорбированного вещества зависит не только от концентрации с, но и от насыщенности, а = а (с, s). Ограничимся основным случаем FiC(c° — со) < 0. Прямое обобщение изложенной
процедуры заключается в том, что решение строится «слева направо», т. е. от малых значений
Пусть решение «достроено» до точки (s-, с~, F~), ЇГ = min Будем искать его продолжение как «скачок» (может быть, бесконечно малый скачок), обеспечивающий минимальное значение скорости I,.
Из условий на нем
' s± — s - s+ + (A? +ДЛ)(Дс—Ду)-1
Получаем два независимых уравнения для определения с+ и s+. Если единственное решение этих уравнений есть с+ = с~, s+ = s~, данный участок решения представляется s - или с-волной и следующий шаг должен быть бесконечно малым (практически равным шагу численного интегрирования) в соответствии с уравнением
DF/ds = (V.77)
Если же система (V.76) имеет нетривиальное решение со < с+< < с~, s+, то производится скачок в точку s+, F (s+, с+), после чего построение решения продолжается по тому же алгоритму вплоть до достижения концентрации с0. Если Ff с (с0 — Со) > 0, то аналогичное построение проводится справа налево (от больших значений? к меньшим) с выбором на каждом шаге £+ = £/ = max (Мг)-
Фронтальное вытеснение. Неавтомодельные решения. Вытеснение оторочкой активной примеси. Запаздывающее воздействие. Анализ автомодельных движений не исчерпывает гидродинамического исследования процессов вытеснения нефти растворами активных примесей. Из числа неавтомодельных движений, которые также удается изучить в рамках изложенного общего подхода, наибольший практический интерес представляют вытеснение нефти оторочкой раствора активной примеси и закачка активного агента с запаздыванием воздействия на пласт. В настоящее время эти задачи интенсивно исследуются. Рассмотрим методику решения и ее возможности.
Оторочкой обычно называют имеющую конечный объем порцию раствора активного агента, который закачивается на начальной стадии вытеснения, а затем проталкивается по пласту водой. Основной смысл использования оторочек состоит в экономии дорогостоящих химических реагентов при сохранении повышенной нефтеотдачи с применением химических реагентов при заводнении. Формально задача о фронтальном вытеснении нефти оторочкой активной примеси в крупномасштабном приближении сводится к решению системы уравнений (V.47) при начальных и граничных условиях.
S (х, 0) = s0. с (х, 0) = 0; F(s, с)\х=0 = 0, с(0, t) = c°, 0<t<T, с(0, 0 = 0, t>T. (V.78)
Очевидно, что до момента t = Т решение сформулированной задачи совпадает с рассмотренным автомодельным решением. В момент
|
|
|
РИС. 64. К задаче о вытеснении нефти оторочкой активной примеси |
T = Т на границе х = 0 появляется скачок концентрации. При і > Т распространяющееся от него возмущение взаимодействует с центрированной волной, примыкающей в автомодельном решении ко входу пласта. Ограничимся простейшим вариантом задачи, когда изотермы сорбции а (с) и распределения примеси 9 (с) линейны:
А = шТс, f = <рос. (V.79)
В этом случае, как легко установить, прямой и обратный скачки концентрации распространяются без искажения; мгновенная скорость скачка в каждый момент
|
V = |
U F+ — F - _ U f± + 90/(l— 90)
(V.80)
.5- m s± (еро + Г)/'(і — 90) Таким образом, на (s, ^-диаграмме каждому сопряженному s, с скачку соответствует, как и в автомодельном решении, переход по лучу, проходящему через ПОЛЮС (—Sp, —Fp), с одной из кривых F (s, 0), F (s, с0) на другую.
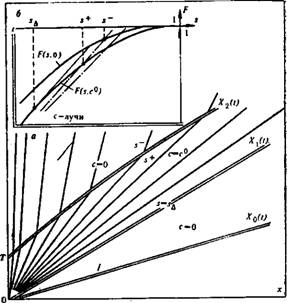
Проведем на плоскости (х, t) траектории скачков: Хо (t) — переднего скачка насыщенности; X\(t) и Х2 (і) — переднего и заднего сопряженных скачков насыщенности и концентрации (рис. 64). Рассмотрим траекторию заднего скачка, распространяющегося по центрированной волне отвечающей автомодельному решению так, что X2=(U/m)F, s(s+, c°)t, (V.81)
|
DX2 ИГ |
|
S+ |
Где s+ — насыщенность перед скачком. С другой стороны, из условий (V.80)
С+ -- с
__ и F (s+, c°)+Fp
(V.82)
Подставляя (V.82) в (V.81), получим
|
(V.83) |
|
T = Тех p |
F___________ f"(s, c°)ds
J v'i. Ж Г* Л. ^
F'ls, c°)-[F(s, C°) + Fp]/(,_S,)
S*
Соотношение (V.83) устанавливает зависимость от времени насыщенности s+ перед вторым сопряженным скачком. Координаты и скорость скачка определяются соотношениями
Х2 = (Vim) F' (s+, с°) t, V = (Ulm) [F (s+) + Fp] (s+ + sp)-'. (V.84)
Из (V.83) и (V.84) видно, что по мере распространения второго скачка его скорость постепенно увеличивается и стремится к скорости первого сопряженного скачка F' (sa); насыщенность перед фронтом постепенно убывает и стремится к Яд при / -»■ оо; она в каждой точке меньше скорости соответствующей характеристики F' (s+). Отсюда следует, что второй скачок не влияет на условия распространения первого сопряженного скачка и на решение при x>Xl(t).
Расстояние между скачками равно
L (t) = X, (/) - Х2 (0 = (Ulm) t [F' (5д) - F' (s+)]. (V.85)
Используя (V.83), легко показать, что существует конечный предел L (со) = L„. Таким образом, асимптотически при t оо формируется стационарная оторочка, движущаяся со скоростью, равной скорости первого сопряженного скачка Vi = (Ulm) F' (s4). Чтобы построить решение в области за вторым скачком, заметим, что из последнего условия (V.80) можно найти величину s~ (t) — проще всего это сделать графически (см. рис. 64). Легко видеть из рис. 64, что sa скачком (х = Х2— 0) оба семейства характеристик уходят со скачка. Поэтому решение в области х < Х2 (t) определяется полностью начальными данными на линии х = Х2 (t) и описывается уравнением
X (t, s) = Х2 (U, s) + F' (s, 0) (Ulm) (t —12 (s)). (V.86)
Здесь в качестве параметра на линии х = Х2 (t) взята насыщенность непосредственно за скачком, s = s~; Х2 и t2 — соответствующие значения координаты скачка и времени.
Естественно поставить вопрос об асимптотике решения при больших временах. Ее можно получить, рассматривая предел полученного выше решения. Можно, однако, рассуждать и по-другому. Как было показано, со временем оторочка стабилизируется и начинает двигаться с постоянной скоростью. Поэтому будем искать в подвижной системе координат, связанной с оторочкой, стационарное решение вида
S = 5 (ig), с = С (kj), - ц = х — Vt, СМ = 0, |Ч|>/, Cfo) = c°, Ы</. (V.87)
Подставляя выражения (V.87) в основную систему (V.47), получим:
= 0, —UF + mVS = const,,
__у d[mcs + m(\ — s) у + о] , у d [cF + у (1 — f)]
Dri dri » \ ■ /
— [mcs + m«p (1 — s) + a] V + U [cF + ? (1 — F)] = const2.
Как нетрудно видеть, условия (V.88) показывают, что значения насыщенностей перед оторочкой s+ и за ней s~ связаны между собой и со скоростью V условием на скачке:
MV/U = (F+ — F~)/(s+ — s-). (V.89)
При этом значение s внутри оторочки определяется пересечением прямой, соединяющей точки М+ (s+, F+) и М~ (s~, F~) с кривой F = F(s, c°).
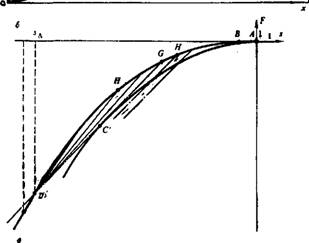
Второе уравнение (V.88) показывает, что прямая М+М~ проходит через полюс (—sp, —Fp). Наконец, учитывая условия устойчивости переднего и заднего фронтов оторочки, легко убедиться, что прямая М+М~ должна быть касательной к кривой F(s, с0), чем положение этой прямой и всех элементов решения определяется однозначно. Построенное инвариантное решение типа равномерно распространяющейся волны с точки зрения задачи в целом представляет собой внутреннюю асимптотику решения, отвечающую малости объема оторочки или — что эквивалентно — большим временам наблюдения. Внешним решением задачи при этом, как легко видеть, будет решение задачи двухфазной фильтрации в отсутствие активной примеси (с = 0) с дополнительным скачком насыщенности, обусловленным наличием тонкой оторочки. Положение этого скачка определяется величинами s+ и s~, определяемыми из внутреннего решения. На (s, ^-диаграмме ему соответствует путь ABGDE. Полученный результат заслуживает особого комментария. Дело, в том, что автомодельное решение задачи вытеснения нефти водой, соответствующее пути ABGDE, существует и в отсутствие активной примеси; однако оно неустойчиво. Таким образом, роль тонкой оторочки активной примеси формально сводится к стабилизации неустойчивого решения, отвечающего рис. 59, г.. При этом, очевидно, ширина оторочки имеет второстепенное значение, а главную роль играет та максимальная степень снижения подвижности воды, которая достигается в оторочке. Если активная примесь «полезная», то FtC < 0, и последнее утверждение означает, что целесообразно использовать максимальные значения концентрации примеси в оторочке.
Та же техника позволяет проанализировать влияние запаздывания закачки активного агента на показатели разработки. Запаздывание достаточно часто происходит по техническим причинам. Будем считать, что пласт, первоначально однородно насыщенный нефтью,
с момента t = О разрабатывается заводнением, а при і = Т начинается закачка активной примеси. Этим условиям отвечает задача
S(x, 0) = so, с(х, 0) = со, s (0, 0 = s° [с (0, *)]; с(0, 0 = 0, 0 <t<T, с(0, 0==с°, Т <t< оо (V.90)
Для уравнений (V.47).
Вплоть до t Т имеем обычное решение Баклея — Леверетта в виде центрированной волны, заканчивающейся скачком:
S = s($), £ = xmlUt, 0 < £ < £о, S = s0, 6 > ?0. (V.91)
|
(V.92) |
|
(- |
|
•эр, |
При t ~ Т от границы пласта внутрь него начинает перемещаться поверхность разрыва концентрации и насыщенности, причем мы будем полагать выполненными условия распространения скачка без размывания, так что
С = с0 = 0, х> Хс (0, с — с0, х < Xc(t).
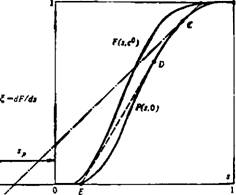
Из соотношений на сопряженном скачке (V.52) — (V.53) следует, что на (s, /^-диаграмме скачок соответствует переходу с кривой F(s, 0) на кривую F (s, с0) по с-лучу, проходящему через полюс
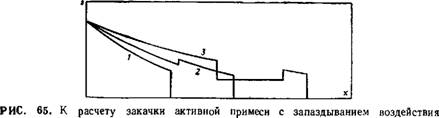
-Fp) (рис. 65). Последовательным положениям скачков отве
Чает переход по пучку с-лучеи справа налево, начиная от положения В, отвечающего образованию скачка, и вплоть до предельного положения GC'D'. При этом из рис. 65 видно, что скорость скачка все время выше характеристических скоростей перед ним. Скачок взаимодействует с центрированной волной, а распределение насыщенности за ним определяется уходящими с него характеристиками. Учитывая это обстоятельство и условия на скачке, имеем:
DXc/dt = {Ulm) [F (s+, 0) + Fp]/(s+ + sp),
Xc = (U/m) F' (s+, 0) t, Xc (T) = 0. (V.93)
Отсюда получаем
|
A -I |
|
T = T exp |
|
(V.94) |
F"(s, 0) ds
[F (s, 0) + Fp] (s + sp)—1 F' (s, 0)
|
При этом значение из уравнения |
Насыщенности за скачком s~ определяется
|
S~ (і) + (0 + s„ |
|
(V.95) |
F(s-(0, с0) = (F(s+ (0, 0) + Fp) ■
Решение (V.94) — (V.95) сохраняет смысл до тех пор, пока с-луч не совпадет с касательной к кривой F (s, со) s+ = st (см. рис. 65). После этого скорость с-скачка перестает меняться, и перед ним формируется дополнительный «обратный» s-скачок, взаимодействующий с первоначальной центрированной волной. На (s, ^-диаграмме ему отвечает переход из фиксированной точки D' в переменную
|
|
|
На пласт Точку Н, соответствующую значениям параметров в центрированной волне. Поэтому движение этого скачка определяется уравнениями dXJdt = (U/m) [F (s+) - F (si)]/(s+ - s4); F(s) =F (s, 0), Xs = (U/m)F'(s+)t, Xs{h) = Xc(h), s+(h) = sЛ. (V.96) |
____________ F" (s) ds_________
|
Отсюда имеем / = /д ехр |
|
S4 |
|
(V.97) |
|
S+ |
[F (s)-F(s^)](s-s,)-i~F' (s)
Ограничимся здесь только случаем, когда насыщенность sA больше фронтальной в первичной центрированной волне, отвечающей решению Баклея—Леверетта. При этом решение (V.97) сохраняет смысл вплоть до t — со; амплитуда обратного скачка асимптотически стремится к нулю, а решение асимптотически стремится к автомодельному решению, отвечающему Т = 0. Эволюция мгновенных профилей насыщенности во времени показана схематически на рис. 65, в.
Изложенный в этом пункте материал, в основном, содержится в [18]; подход к исследованию неавтомодельных задач берет начало от работы П. Г. Бедриковецкого по вытеснению нефти оторочками активных примесей [8]; задача запаздывающего вытеснения исследована О. М. Алишаевой и А. Ф. Зазовским.