ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Нестационарные задачи фильтрации неньютоновских жидкостей
Нестационарные процессы в пластовой системе при фильтрации неньютоновских жидкостей обладают определенными особенностями, позволяющими в некоторых случаях обнаружить нарушения закона Дарси, оценить их количественно и дать прогноз их возможного влияния на показатели разработки нефтяного месторождения. Поэтому наблюдение нестационарных процессов — важный источник информации о свойствах пластовой системы.
Основные уравнения. Пусть Р (х, у, z) — распределение давления, отвечающее некоторому стационарному фильтрационному движению, а р (х, у, z, t) — распределение давления в нестационарном процессе, начинающемся в момент t — 0, причем
Р (х, у, г, 0) = P. (II 1.62)
Разность
Р=р — Р (III.63)
Назовем возмущением давления или отклонением от стационарного состояния.
Комбинируя уравнения неразрывности слабосжимаемой жидкости
M/C-[7]A<+dive = 0 (III.64)
И закона фильтрации, которое запишем в виде
Gradр = —ПФ (ы/Х) и! и, и = —Х<|» (| Vp |/П) vp/| vp | (III.65)
(П — характерное значение градиента давления; X — характерное значение скорости фильтрации), получаем систему уравнений фильтрации неньютоновской жидкости при упругом режиме, которую можно привести к одному уравнению
Стационарное распределение, для которого p, t =0, также удовлетворяет уравнению (III.66) или системе (III.64) — (III.65).
Однако р, будучи разностью двух решений уравнения (III.66), вообще говоря, из-за нелинейности функций Ф и не является решением. Таким образом, при нелинейной фильтрации несправедлив принцип суперпозиции решений, и характер возмущений зависит, вообще говоря, не только от свойств пластовой системы и инициирующих возмущение внешних воздействий (например, пуск скважины), но и от начального состояния. Далее в тех случаях, когда особо не оговорено противное, будем считать начальное состояние отвечающим первоначально невозмущенному пласту [Р = Р0 =const), причем в силу того, что в уравнения (III.64)— (III.66) давление^ входит только под знаком производных, можно положить Ро = 0, р=р.
Бегущая волна. При распространении возмущения с той или иной степенью строгости выделяется фронт возмущения, отделяющий невозмущенную область от области возмущения.
Выберем вблизи фронта возмущения некоторую малую область, движущуюся со скоростью фронта. В силу малости области распределение давления в ней можно в любой момент считать стационарным
Будем искать поэтому решение уравнений (111.64) — (III.65), соответствующее бегущей (равномерно распространяющейся в направлении оси Ох) волне:
Р = р (x — Vt), и = и(»), \ = х — Vt. (III.67)
|
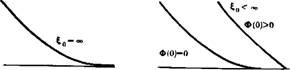
РИС. 28. Распределение о |
|
|
|
Б |
|
Волны: а—с бесконечной скоростью распространения; б — с конечной скоростью распространения |
|
Давления вблизи фронта возмущения при нелинейной фильтрации. |
|
Подставляя выражения (III.67) в систему (III.64) — (III.65), получим
|
|
(111.68) |
Откуда
DU/dX = — (U), U = «/X, v = mVR/lK, X = —о(t/)/v, р = IIVh + Р-, a(t/) = J[®(t/)]-IrfЈ/. (III.69)
Из очевидных условий на бесконечности р = и = 0, $ оо получаем р„ = 0. Дальнейшие выводы существенно зависят от характера закона фильтрации. Если Ф (U) при U -> 0 остается конечным либо стремится к нулю достаточно медленно (например, как Us, s< 1), то интеграл в (III.69) сходится на нижнем пределе и, следовательно, существует граница X = на которой и правее ее р = и = 0, т. е. волна распространяется с конечной скоростью. В силу произвола в выборе начала отсчета X будем полагать Хо = 0. Вблизи фронта волны X = £о производная dl/dU обращается в бесконечность, если Ф (0) = 0 (предельный градиент давления отсутствует), и конечна при фильтрации с предельным градиентом. Таким образом, на переднем фронте волны давление и скорость фильтрации обращаются в нуль плавно, если предельного градиента нет; при наличии предельного градиента на фронте волны распределение давления имеет угловую точку (рис. £8;.
Устремим теперь U к бесконечности. При ЭТОМ, если а (со) = оо, то X —оо; если же а(оо)< со (так будет, например, при Ф (U) — ~ С > 1), то давление и скорость фильтрации в равномерно движущейся волне обращаются в бесконечность в конечной точке. Выбрав точку, совпадающую в начальный момент с фронтом волны, за входное сечение (х = 0) пласта и полагая в полученных соотношениях X = —Vt, найдем, по какому закону нужно менять во времени давление в этом сечении для того, чтобы волна в пласте двигалась равномерно. Обращение этого давления в бесконечность за конечное время означает, что добиться равномерного движения волны давления в течение более длительного времени невозможно; она должна начать замедляться.
В рассмотренном решении наиболее существенным моментом является характер изменения давления и скорости фильтрации вблизи фронта волны. Скорость распространения возмущений конечна, если интеграл (III.69) сходится на нижнем пределе (в частности, при законе фильтрации с предельным градиентом), и
распределение давления имеет на фронте угловую точку, Ф(0)=^0, причем при приближении к границе из области движения градиент давления стремится к предельному. Эти существенно для правильного понимания качественных особенностей решения и для их приближенного построения выводы подтверждаются анализом известных решений более сложных задач. В некоторых случаях такие выводы можно строго обосновать.
|
1 П дг |
Течение вблизи скважины. При исследовании пластов наибольший интерес представляют течения вблизи возыуща - ющей скважины. Считая начальное состояние пласта невозмущенным, имеем одномерное плоско-радиальное течение, определяем соотношениями
Др_ _ /а_1_ А
Ді т г дг
Р (г, 0) = 0; lim[2i:r/AV(II->/>.,)] = Q(/) или /? (р, f) = pw (III.70)
R-0
(при условиях задания на скважине дебита или давления соответственно). Указанная задача автомодельна в следующих случаях. 1) при степенном законе фильтрации; 2) при произвольном зако не фильтрации, если дебит изменяется по закону Q=AtV - (см. далее задачу 1). Поскольку этим условиям не удовлетворяю практически важные задачи, их приходится исследовать либо приближенно методом интегральных соотношений (см. гл. II), либо численно.
Для отыскания приближенного решения задачи (III.70) примем распределение скоростей фильтрации в виде
Где l{t) — граница зоны возмущения. Выберем l(t) таким образом, чтобы в каждый момент удовлетворялось следующее из (III.70) первое интегральное соотношение: соотношение материального баланса
ЖІ^Г-Р^ t)dr=-Q(f). (111.72)
О
Здесь с учетом условия р (I, t) — 0 вместо р (г, t) следует подставить выражение
Т
P(r, t) = - J ПФ(|Ц((' (III.73)
Где и (г, t) дается соотношением (III.71). Выражение (111.71) для скорости фильтрации правильно отражает особенности распределения ее вблизи скважины и на границе зоны возмущения. Поэтому можно получить при таком приближенном решении достаточную точность.
В частности, для закона фильтрации с предельным градиентом при Q = const получим (П = G, X = kG/p, Ф(і/) = U+l):
^o-SK+t'-^O-f)].'*'.
P + 2P/l* = 12*/, /* = IxQ (2rMG)-\ * = kK/mp,
P* = p(Р-О^ІіК + '-т) (IIL74)
На рассматриваемом примере отчетливо видна роль, которую играет дополнительный размерный параметр — предельный градиент давления G. В комбинации с дебитом на единицу мощности пласта с помощью этого параметра получаются характерный линейный размер /* и характерное время t* = /*2/х.
Решение задачи оказывается качественно различным при 1
И > 1. При малых временах имеем I < Пренебрегая в (II 1.75) членами порядка ///*, можно убедиться, что формально это эквивалентно предположению G = 0, т. е. при малых временах решение задачи фильтрации с предельным градиентом оказывается подобным решению линейной задачи:
= 1п т?; 1 = (12х^1/2«<IIL75>
Причина такого совпадения решений линейной и нелинейной задач состоит в том, что при малых временах изменение давления происходит в узкой зоне, где градиенты давления весьма велики; при таких обстоятельствах поправка, вносимая предельным градиентом, пренебрежимо мала. Со временем область движения расширяется, и все большую долю ее составляет область малых градиентов (напомним, что скорость фильтрации на расстоянии г от скважины, очевидно, не превосходит Q!(2r. rh). Поэтому все более существенным оказывается вид закона фильтрации при малых скоростях. Если t > t*, имеем
1 I r. khG J '*' ~ /3^(х(ЗУ/3 , pQ, %khGр3 , 3ixQ /TTI _с.
Таким образом, для значительных времен закон изменения давления в скважине оказывается уже не логарифмическим, а степенным. График pw(In t) показан на рис. 29, распределение давления в функции от расстояния от скважины имеет логарифмическую асимптотику вблизи скважины, а на границе зоны возмущения градиент давления равен предельному.
Позднее вернемся к анализу найденного решения. Воспользуемся тем же приближенным подходом для того, чтобы рассмотреть пуск скважины с постоянным забойным давлением pw = P°w < 0. Приняв вновь приближенное распределение скорости фильтрации в виде (III.71), после несложных выкладок получим
Q{t) = _^iPw + Gl)/(inj—l); P»>-G/;P«/,
+ = (III.77)
Где p — радиус скважины.
Последние соотношения приводятся к обыкновенному дифференциальному уравнению первого порядка для I. При малых временах, р < / < —A»/G предельный градиент давления не проявляется. При этом
/^(12х01/2> Q ~ — 2vkhPw/^ ln(//p). (III.78)
С другой стороны, при I -> —Pw/G = дебит Q О, и из (111.77) легко находим, что с увеличением времени (t со) граница зоны возмущения асимптотически стремится к Iраспределение давления при этом стремится к предельному
P-(r) = Pw + (r — 9)G, r<L. (III.79)
При этом дебит Q с возрастанием t стремится к нулю экспоненциально, и, следовательно, суммарный отбор жидкости из скважины V за бесконечное время при фиксированной депрессии Pw конечен. Этому соответствуют конечность воронки депрессии и области дренирования скважины после прекращения притока. Из соображений баланса находим предельный суммарный отбор жидкости из скважины
,, с" 2nhmr.. , ЧлтЬ. Ръ.... от
= і (г) = Тте5" ( }
Конечность зоны дренирования может приводить к заметному снижению степени извлечения жидкости из пласта при разработке на истощение. Имеется ряд указаний на то, что этот эффект существен при разработке также и газовых месторождений, приуроченных к глинизированным коллекторам, когда для газа обнаруживается пороговый градиент давления (см. далее задачу 3).
Взаимодействие возмущений с внешним потоком. Взаимодействие эффектов нелинейной фильтрации и неоднородности фильтрационного потока может определяющим образом влиять на характер нестационарных процессов. Из всего многообразия возникающих здесь вопросов мы рассмотрим только влияние внешнего потока на распространение возмущений от скважины. Поскольку в данном случае речь идет, главным обра
зом, о сложных двумерных течениях, ниже приводятся в основном результаты численного решения соответствующих задач. Однако некоторые существенные моменты удается обнаружить на следующем сравнительно простом примере. Допустим, что в начальный момент в пласте существует стационарное течение без застойных зон (ы>0), которому отвечает распределение Р(х, у, z) а в момент / = 0 начинается нестационарный процесс, характеризуемый возмущением давления р (х, у, z, t). Будем полагать это возмущение малым, так что в любой точке пласта
Wl«lvn
|
Тогда для возмущений давления р можно получить приближенное линейное уравнение, если подставить в (III.66) р = Р+р и провести разложение по степеням р, ограничившись линейными членами. Учитывая, что Р—решение уравнения (III.66), получим, очевидно,
Напомним, что Р (х, у, г) считается здесь известным, так что (II 1.82) представляет собой линейное параболическое уравнение |
Относительно возмущения р. В частности, если невозмущенное течение представляет собой однородный поток с градиентом давления П0, уравнение (II 1.82) принимает вид
(III.83)
Уравнение (III.83) — линейное уравнение теплопроводности в анизотропной среде с коэффициентами проводимости, различными по осям х и у. Коэффициенты проводимости составляют: *о по оси у И Хо'Ро/ЧГо по оси х. Их отношение равно отношению угловых коэффициентов касательной к кривой ЧГ (С) в точке С = П0/П и секущей, проведенной из начала координат в ту же точку. Для псевдопластического характера закона фильтрации (Ф" > 0) это отношение всегда больше единицы. Вообще говоря, оно зависит от интенсивности невозмущенного течения и, в частности, для закона фильтрации с предельным градиентом (<Р(С) = С—1, П = G) монотонно убывает от бесконечности до единицы с ростом интенсивности течения от П = G до бесконечности.
|
(III.81) |
|
|
Нетрудно убедиться непосредственно в том, что локально в каждой точке неоднородного потока структура уравнения для возмущений будет близка к (III.83), если под х и у понимать оси, ориентированные по невозмущенному потоку и по нормали к нему.
Уравнение (II 1.83) преобразованием
|
|
(III.84)
В частности, если начальное возмущение создается в начале координат (х = у = 0), то в системе XOY задача осесимметрична:
Р = p(R, t); R2 = X2 + Y2. (III.85)
С учетом (III.84) это означает, что в исходной системе хОу линии уровня возмущения р(х, у, t) — эллипсы, определяемые уравнением {x/w'o)2 + (y/Vof = const. (III.86)
Следовательно, возмущение давления распространяется по однородному начальному потоку с различной скоростью в разных направлениях — нестационарный процесс обладает «наведенной анизотропией». Приведенный анализ нельзя непосредственно использовать для исследования основной задачи о возмущении однородного потока при пуске скважины, поскольку в этом случае возмущения градиента давления вблизи скважины не малы. Однако можно ожидать, что характер изменения давления качественно будет таким же, как и в рассмотренной линеаризованной задаче.
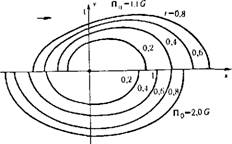
Численные расчеты[8] возмущения, вносимого в однородный фильтрационный поток пущенной в работу скважиной, в основном подтверждают эти предположения. На рис. 30 показано распространение линии уровня возмущения, отвечающей /7 = 0,05 QG/K при различных значениях интенсивности исходного потока.
Помимо предсказанной нами заранее анизотропии распространения возмущений (тем сильнее выраженной, чем меньше интенсивность внешнего потока) наблюдается и своеобразный их «снос» внешним потоком. Этот существенно нелинейный эффект объясняется тем, что внешний поток и поток от скважины с одной стороны от нее (см. рис. 30, слева) противоположно направлены, в результате чего образуется застойная зона. Последствия такого локализованного вблизи скважины взаимодействия проявляются и на удалении от нее, где линии уровня давления оказываются смещенными по потоку.
Анализ динамики изменения давления в скважине при пуске ее в работу показывает, что внешний поток может оказывать на нее существенное влияние. Из рис. 29 видно, прежде всего, что достаточно сравнительно слабого внешнего потока для того, чтобы кривая изменения давления (т. е. зависимость давления в скважине от времени) стала существенно отличной от кривой, рассчитанной для осесимметричного притока в невозмущенном пласте. С увеличением интенсивности внешнего потока это различие растет, и кривая изменения давления приближается к кривой, отвечающей линейному закону фильтрации.
Анализ данных исследования скважин. Как уже говорилось, основная цель исследования нестационарных
процесов состоит в том, чтобы дать методы определения параметров пластов по данным исследования скважин. В тех случаях, когда речь идет о течениях, не следующих закону Дарси, эта задача, непростая сама по себе, становится особенно трудной.
Главная трудность состоит в том, что нельзя заранее указать, какого рода отклонения от идеальной модели упругого режима фильтрации присущи исследуемому объекту. Так, искривление индикаторных диаграмм скважин может быть вызвано не только нелинейностью закона фильтрации, но и разгазированием нефти, нелинейно-упругой деформацией пласта в целом или раскрытием трещин в прискважинной зоне и т. д. Далее, если даже установлено, что нелинейность обусловлена нарушением закона Дарси, остается проблема выбора между, допустим, законом фильтрации с предельным градиентом давления и степенным законом фильтрации.
В настоящее время нет законченной методики анализа результатов наблюдений, позволяющей решать сформулированную выше проблему выбора. Более того, уже ясно, что такая методика не может быть чисто гидродинамической, а должна использовать всю совокупность сведений о пласте для уменьшения числа конкурирующих гипотез.
Ниже рассматривается только вопрос о различении эффектов нарушения закона Дарси и нелинейно-упругого режима по данным исследования скважин. Этот вопрос был детально исследован в последнее время численно.
Рассматривается пуск в работу скважины в первоначально невозмущенном пласте с постоянным начальным давлением Р0, причем предполагается, что проницаемость k и пористость т зависят от давления и использована экспоненциальная аппроксимация
K (р) = k0 exp \ak (р — Ро)]; т (р) = т0 exp [ат (р — Ро)]- (И 1.87)
Одновременно допускается, что движение следует закону фильтрации с предельным градиентом вида (111.9) с постоянным значением G. Были рассмотрены различные режимы изменения дебита скважины во времени и соответствующие им режимы изменения давления в скважине и на удалении от нее.
|
РИС. 30. Распространение линий уровня возмущений от скважины при наличии однородного внешнего потока |
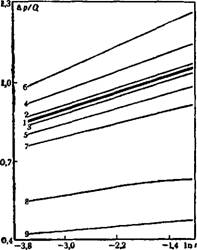
На рис. 31 показаны кривые относительного изменения давления Лр/Q при пуске скважины с постоянным дебитом при нелинейно - упругом режиме (G = 0) и слабо меняющейся пористости (ат = 0>
для различных значений единственного безразмерного параметра задачи (Q > О отвечает закачке, Q < 0 — отбору жидкости)
С ростом параметра А относительное изменение давления уменьшается. Если учесть, что в широком диапазоне изменения А зависимость Др/Q от In t достаточно близка к линейной (см. рис. 31), то при любой интерпретации результатов исследований с ростом интенсивности закачки увеличивается эффективная гидропроводность пласта (fc/i/ji), определенная по кривым изменения давления (соответственно уменьшается гидропроводность с увеличением интенсивности отбора).
Если не учитывать зависимости проницаемости и пористости от давления, но считать закон фильтрации нелинейным псевдопластическим (рост относительной подвижности с ростом скорости фильтрации, Ф"(С/)<0), то анализ кривых изменения давления при пуске скважины по стандартной методике [11] приводит к выводу, что эффективная гидропроводность возрастает с увеличением абсолютного значения дебита, при котором проведено исследование скважины. Причем, если закон фильтрации аппроксимируется степенной зависимостью Ф(U) = US, то зависимость эффектной гидропроводности от дебита также степенная:
(£%)эф~|<21с, С = 2 (s— 1)/(3 — s). (III.88)
Таким образом, основное отличие между эффектами нелинейно-упругого режима и нелинейной фильтрации при исследовании
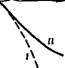
Скважин проявляется в том, что первым соответствует рост эффективной гидропроводности с ростом дебита при закачке и падение при отборе; вторым — рост гидропроводности с ростом дебита как для закачки, так и для отбора (рис. 32). Легко убедиться, что это — общий факт, не зависящий от принятых аппроксимаций. Такое отличие служит своего рода «диагностическим признаком» для различения двух причин нелинейности.
Можно предположить методику выделения каждого из этих эффектов, выделяя четную и нечетную по Q части зависимости Ap/Q от Q.
|
РИС. 31. Кривые относительного изменения давления. Значения А: 1—0; 2----------- 0,03; 3—0,03; 4------- 0,15; 5 — 0,15; 6-------------- 0,3; 7 — 0,3; « — 1,5; 9 — 3,0
|
Другим важным диагносциру - ющим признаком может быть характер распространения возмуще - ний на больших расстояниях от
|
4 р |
|
|
РИС. 32. Изменение эффективной гидропровод - ности при нелинейно-упругом режиме (/) и нелинейной фильтрации (//)
Скважины. В этой области давление мало отклоняется от невозмущенного, а скорости фильтрации близки к нулю. Поэтому очевидно, что здесь нелинейно-упругие эффекты слабы, а эффекты нелинейной фильтрации, в особенности типа предельного градиента давления, выражены особенно сильно. Так, на рис. 33 показано изменение давления на различных расстояниях от возмущающей скважины при периодическом (со сменой знака) изменении дебита в ней.
Помимо относительно быстрого затухания возмущений и конечности расстояния, на которое они распространяются, существенно, что с растоянием последовательные импульсы давления не сглаживаются, а все более приближаются по форме к прямоугольным. Этот качественный признак можно использовать для установления наличия в пластовых условиях предельного градиента давления.
Задача 1. Показать, что решение задачи о притоке к скважине, пущенной в работу с постоянным дебитом Q, автомодельно при степенном законе фильтрации. Исследовать зависимость давления в точке наблюдения от времени. Получить зависимость (III.88).
Задача 2. Объяснить качественно эффект перестройки импульсов в прямоугольные при фильтрации с предельным градиентом.
Задача 3. Определить максимальный возможный отбор газа в расчете на одну скважину, если начальное пластовое давление р0, минимально допустимое давление на забое р и движение газа следует закону фильтрации
^=-4~(Vp2-nVp2J\Vp2\); | Vp2 | > п, pu = 0, IV/f2 1 < п.