ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Теория фильтрации неньютоновских жидкостей. Закон фильтрации
|
(III.1) |
Неньютоновские жидкости. Аномальными или неньютоновскими называются жидкости, не следующие классической модели вязкой жидкости [35]. Наиболее простые из них нелинейно-вязкие жидкости, для которых девиатор тензора напряжений однозначно определяется девиатором тензора скоростей деформаций, они соосны, но зависимость между ними нелинейна. При простом сдвиге это проявляется в нелинейности кривой течения, связывающей касательное напряжение т и скорость сдвига f
(рис. 17):
X = F(T); Т=Г(х).
Нас будут прежде всего интересовать структурирующиеся нелинейно-вязкие жидкости, способные образовывать твердообразные структуры, разрушающиеся при увеличении интенсивности деформации. Такие жидкости являются псевдопластическими: кривая 7 = Г(т) для них выпукла к оси т: Г"(х)>0. Крайнее проявление псевдопластичности описывается известной моделью
|
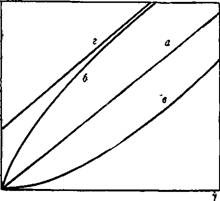
РИС. 17. Кривые течения ньютоновской (а), псевдопластической (б), дилатантной (в) и бингамовской (г) жидкостей
|
|
* |
Вязко-пластической жидкости, определяемой соотношениями Бингама — Шведова:
У = 7J-1 (х — Тр), Х>Х0,
(III.2)
Здесь То — предельное напряжение сдвига; г| — структурная вязкость.
Для описания экспериментальных данных, особенно в небольшом диапазоне изменения переменных, часто используется и степенная зависимость вида
Х = K'f. (III.3)
Для ряда аномальных систем модель нелинейно-вязкой жидкости оказывается непригодной. Если напряжения зависят не только от текущего значения тензора скоростей деформации, но и от предыстории деформирования данного жидкого элемента, вполне ею определяясь, то такая жидкость называется простой. Частный случай простых жидкостей — упруго-вязкие жидкости, например, простейшая линейная жидкость Максвелла, для которой связь между т и у при простом сдвиге определяется дифференциальным уравнением
|лТ' = т+Єт. (III.4)
Где постоянная величина 9 называется временем релаксации. Очевидно, при медленном изменении напряжений тело Максвелла подобно ньютоновской жидкости с вязкостью ц, а при быстром — упругому телу с модулем сдвига G = n/0. При движении упругих жидкостей могут накапливаться большие упругие деформации. В результате реологические аномалии упруго-вязких жидкостей проявляются по-разному при сдвиговом течении (например, в зазоре вискозиметра), когда эффективная вязкость уменьшается с ростом скорости сдвига, и при одноосном растяжении. В последнем случае при достаточно больших скоростях деформации «продольная вязкость» жидкости, определяемая по отношению действующего в сечении напряжения к скорости удлинения, резко возрастает.
Заметим, что все сказанное выше относилось к несжимаемым или капельно-сжимаемым жидкостям, и, скажем, упругость жидкости — это сдвиговая упругость, которая может не иметь ничего общего с объемной упругостью (сжимаемостью) жидкости. Особенно важно, что характерные значения модулей сдвига G могут быть на много порядков меньше модуля объемного сжатия Ку. Так, для используемых в процессах повышения нефтеотдачи полимерных растворов значения G и Kv имеют порядки, соответственно, 1 —100 Па и 109 Па = 103 МПа. Это позволяет рассматривать реологию объемных и сдвиговых деформаций независимо.
Наконец, укажем, что в некоторых случаях нам приходится сталкиваться с системами и явлениями, не укладывающимися и в понятие «простой жидкости». Мы имеем здесь в виду в первую очередь системы, имеющие характер коллоидных растворов, внутренняя структура которых может перестраиваться под действием обменных и физико-химических процессов. К таким системам относятся водо-глинистые растворы, ряд растворов полимеров и, по-видимому, некоторые нефти. К сожалению, в большинстве случаев не существует пока адекватного описания таких систем.
Закон фильтрации неньютоновской жидкости. Нелинейно-вязкие системы. Чтобы исследовать проявления неньютоновских эффектов при движении в пористой среде, необходимо прежде всего установить вид закона фильтрации для неньютоновской жидкости. Из-за большого разнообразия аномальных жидкостей единого ответа на этот вопрос не существует.
Наиболее просто обстоит дело для нелинейно-вязких жидкостей. Для них связь между характеристиками течения в пористой среде и стандартной реологией жидкости удается с удовлетворительной точностью получить, моделируя пористую среду системой капилляров, подсчитывая среднюю скорость сдвига и напряжение на стенке капилляра и считая, что эти две величины связаны между собой кривой течения для данного материала.
Обозначим через х^, напряжение на стенке капилляра радиуса R, через ут = U/R = 4Q/kR3 — характерную скорость сдвига. Тогда для течения в капилляре имеем
Ym = 9 Ы = 4х"3 f х2Г (х) dz, (III.5)
О
Где Г (т) — зависимость скорости сдвига от касательного напряжения, определяемая кривой течения. Для описания движения аномальных жидкостей часто пользуются понятием эффективной вязкости Т)5ф
ТЗэф = Iw/l* = W<p (III.6)
Зависящей от скорости сдвига или касательного напряжения.
Для пористой среды среднюю скорость сдвига I'm и среднее касательное напряжение х* можно определять по-разному. Из соображений размерности очевидно, что
F = і (т) u/d, х* = Z(m)d\dp/dx\, (III.7)
Где и—модуль скорости фильтрации; dp/dx— градиент давления; d —внутренний масштаб пористой среды; % и £ — безразмерные функции пористости, обычно определяемые на основе приближенного моделирования порового пространства пучком капилляров. Так, для слоя сферических частиц диаметром D полагают обычно
D = D, х = 12(1 — т)/т2, ; = т/[15(1 — т)].
Эти соотношения переносятся с помощью формулы Козени — Кармана (1.8) на произвольную пористую среду проницаемости k
D = (k/mY'\ х — 0,9/т, С = 0,9.
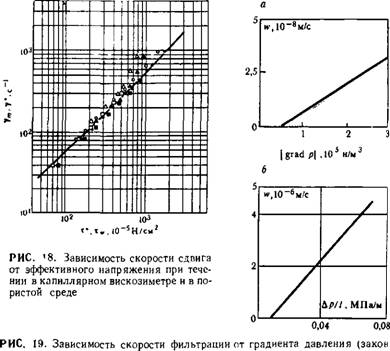
Таким способом для ряда систем получаются вполне приемлемые результаты. Так, на рис. 18 приведены данные для раствора поливинилового спирта [39]. Другие примеры можно найти в обзоре [39], цитированных там статьях и последующих публикациях.
К числу нелинейно-вязких систем, исследованных подробно в последние годы, относятся нефти ряда месторождений Советского Союза. Интерес к их исследованию вызван тем, что было обнаружено, что они при определенных условиях ведут себя как псевдопластические системы. Кривые течения этих нефтей в оп-
|
Фильтрации): А — движение воды в глине: f> — течение вязкопласти ческой нефти через образец пористой среды |
Ределенном диапазоне скоростей сдвига могут быть описаны уравнениями Бингама — Шведова (III. 2).
Достаточно очевидно, что жидкости, обладающие отличным от нуля предельным напряжением сдвига to, могут начать двигаться в пористой среде лишь тогда, когда градиент давления превзойдет некоторое пороговое значение G, называемое начальным или предельным градиентом давления. Из соображений размерности
G^Cz 0&-'/2, (III.8)
Где С — постоянная.
В соответствии с гипотезой о подобии течения в пористой среде и в капилляре особенности движения вязко-пластических жидкостей в пористой среде можно описать соотношениями закона фильтрации с предельным градиентом давления
W = - Ј(Vp-Gvp/| Чр\), | Vp | > G, (ПІ-9)
Г*
W = о, \S7p\<G.
Соотношения (III. 8) и (III. 9) для описания фильтрации вязко-пластических жидкостей были предложены А. X. Мирзаджан - заде [28], причем постоянная С имеет порядок ~10-2. Формула,
аналогичная (III. 9), использовалась как эмпирическое уравнение закона фильтрации воды в глинах (рис. 19).
Сходная «псевдопластическая» картина наблюдается при фильтрации ряда нефтей воды в глинизированных породах, а также при движении обычных ньютоновских жидкостей и газа в глинизированных породах, содержащих остаточную воду.
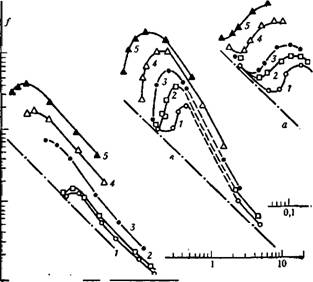
Вязкоупругие эффекты. Часто при попытке предсказать расходную характеристику образца пористой среды по кривой течения жидкости на основе капиллярной модели получаются результаты, не согласующиеся с опытом даже качественно. Весьма характерны в этом отношении многочисленные данные по растворам полиоксиэтилена. На рис. 20 показаны зависимости коэффициента сопротивления f = 64 (Др/fyk/Dpw2 от числа Рейнольдса Re = ayDp/p для раствора полиоксиэтилена WSR-301 с молекулярной массой 3 • 106 ряда концентраций, определяемые из опыта по движению в пористой среде, состоящей из шариков разного диаметра D.
Заметим, что при течении в капилляре эффективная вязкость исследованных растворов остается практически постоянной, так что теоретическая зависимость имеет вид f~Re-1.
При движении в пористой среде «вязкость», начиная с некоторой скорости сдвига, сильно растет и во много раз превосходит начальную вязкость раствора. Подобные же данные получены и
|
|
|
РИС. 20. Зависимость / (Re) для раствора полиоксиэтилена WSR-30I. Концентрация полимера: 1 — \0 ■ 10—6; 2 — 20 • 10—6; — 40 • 10—6; 4 — 80 ■ 10—6; 5 — 160 ■ Ю-6. Диаметр шариков в мм: а — 0,11: в — 0,22; с= 0,45 |
|
10 |
|
10' |
|
JllJ I I I | I I I I I Л 1 I |
|
І...Ц І ЩІІ. |
|
\ \ \ |
|
10 |
|
50 Re |
|
10 |
|
\ \ \V \ |
|
,2 |
|
} |
|
10 |
Для сцементированной пористой среды, а также в опытах по движению полимерных растворов через трубкй переменного радиуса, моделирующие последовательность сужений и расширений поро - вых каналов. Естественно, все эти результаты нельзя объяснить с помощью капиллярной модели пористой среды. Гораздо проще их понять, если учесть, что элемент жидкости в поровом пространстве проходит через последовательность сужений и расширений, и поэтому вынужден изменять свою форму с частотой ~w/mD. Если эта частота становится достаточно большой (wQ/mD~ 1), то существенными становятся упругие эффекты, сопротивление деформации возрастает, и это объясняет наблюдаемое прираще^ ние сопротивления в области достаточно больших скоростей фильтрации. Таким образом, интуитивно легко связать наблюдаемый рост эффективной вязкости с упругостью жидкости. Имеются попытки количественнного расчета этого эффекта. Они основаны на рассмотрении движения в сужениях как аналога растяжения и указывают на известное возрастание вязкости при больших скоростях растяжения как на причину повышенного сопротивления движению упругих жидкостей в пористой среде.
Полимерные растворы, наряду с эффектами вязкоупругости, проявляют при движении в пористой среде и аномалии, обусловленные их микрогетерогенностью и способностью сорбироваться в скелете пористой среды, изменяя ее гидравлическое сопротивление. Это приводит к ряду медленных нестационарных явлений, интенсивно исследуемых в настоящее время [29, 30, 20]. В данной книге мы ограничимся изучением фильтрационных аномалий, связанных с нелинейностью закона фильтрации.