ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Структура течения при мелкомасштабном описании. Стабилизированная зона. Капиллярные эффекты в пористых средах
Стабилизированная зона. При крупномасштабном асимптотическом описании вытеснения несмешивающихся жидкостей воз-
|
0,04 |
|
0,02 |
|
0,5 гГІ s„ |
|
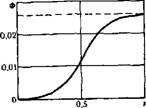
РИС. 41. К построению решения задачи о гравитационной сегрегации на плоскости Ф (s); h = s4; f2-(i+s)x X(l-s)3; ^=1, 0 |
*(s)~
Никают поверхности разрыва—скачки насыщенности. При решении полной системы уравнений (IV. 19) и (IV.20) им соответствуют узкие зоны с большими значениями |grads|. Для описания распределения насыщенности в переходной зоне, соответствующей скачку, введем в окрестности некоторой точки О поверхности разрыва насыщенности локальную декартову систему координат с центром в этой точке. Ось х направим по нормали к поверхности разрыва и введем вдоль этой оси масштаб I — єL, где, как и ранее, є = a2/UoL (ы0 =kAp/\>.\L), т. е. полежим безразмерную координату X равной хЦ, сохранив
Y = y/L, Z = z/L. Масштаб времени примем равным (о = l/Uo = a2/ul и положим т = t/to = ult/a2. Тогда система уравнений (IV. 19), (IV.20) при пренебрежении членами порядка є и выше сведется к следующей:
Д [tp (s) д П /дХ] /дХ = 0, ср (s) д П /дХ = — ш (У, Z, т), (IV.65)
Ds/dz + (ш/т) F (s) ds/dX —д2Ф (s) /дХ2 = 0, <■> = и/и0. (IV.66)
Система уравнений двухфазной фильтрации свелась к одномерной ввиду того, что радиус кривизны поверхности разрыва, определяемый условиями внешнего течения, имеет порядок L и все вторые производные по координатам Y и Z входят в уравнения с коэффициентами, пропорциональными є, а производные по X — с коэффициентами порядка единицы.
В пределах переходной зоны, где течение можно считать одномерным, суммарная скорость ш фильтрации обеих фаз вдоль оси X не зависит от «быстрой» координаты X, а зависит только от «медленных» переменных — времени х и координат на поверхности скачка
Y и Z. Изменение скорости ш происходит за времена порядка L/uq, т. е. большие в масштабе внутреннего разложения. Установление распределения насыщенности вдоль переходной зоны происходит за время t0 = a2/ul, т. е. много быстрее, чем изменение скорости. Поэтому при асимптотическом исследовании течения в переходной зоне (внутреннее разложение) скорость (в можно считать постоянной, а распределение насыщенности — стационарным в координатах, связанных со скачком.
Уравнение (IV.66), описывающее одномерное вытеснение несмеши - вающихся жидкостей с учетом капиллярных сил, называется уравнением Рапопорта — Лиса. Основное значение имеет его решение типа бегущей волны
S - s (С); С = X — V° = V/u0, (IV.67)
Где V — скорость распространения скачка, определяемая из внешнего разложения. Именно это решение описывает распределение насыщенности поперек скачка, поскольку внутренняя структура скачка очень быстро приспосабливается к изменению внешних параметров. В силу большого различия масштабов / и L(/<L) должны выполняться граничные условия сращивания:
S(— оо) = s~ = sc; s (+ оо) = s+ = so, (IV.68)
Где s - = sc и s+ = so — соответственно насыщенности за и перед скачком, определяемые из внешнего разложения. В задаче Баклея —
Леверетта они связаны соотношением (IV. 45). Скорость распространения поверхности разрыва V0 в равенстве (IV.67), определяется формулой (IV.38).
Используя (IV.67), получим вместо (IV.66) уравнение
— mV°ds/d С + <aF' (s) ds/dQ — md [Ф' (s) ds/dQ/dС = 0. (IV.69)
Интегрируя уравнение (IV.69) по С с учетом условий (IV.68) и разрешая относительно dC/ds, имеем
DQds = тФ' (s) / [со (F (s) — F (s0)) — mV° (s — s0)]. (IV.70)
|
С — Сі = |
Отсюда с учетом формулы (IV.38) для скорости скачка V
Ф'(s) ds
[f (s) - F (s,,)] (Se - s0) - [F (scy - F (S„)] (s - s0),
(IV.71)
Где si (so < Si < sc) и Сі — произвольно выбираемое начало отсчета координат. Если скачок стационарный и выполняется условие (IV.45), то вместо (IV.71) имеем
= 2Lf__
|
Ф' (s) ds |
|
С |
|
(IV.72) |
|
-и |
|
F' |
|
F(so) |
|
S0 )' |
|
Sc) (s- |
О) J F (s) -
Формула (IV.72) описывает распределение насыщенности в переходной зоне (рис. 43), которая ввиду стационарного распределения в ней насыщенности традиционно называется стабилизированной зоной. Ширина стабилизированной зоны о определяется как расстояние между точками, насыщенности в которых отличаются от предельных sc и So на некоторую малую величину а0, т. е. как
8 = С (s0 + о0) — С (sc — а0).
В размерных переменных ширина стабилизированной зоны /8 =аЧ/и0, т. е. обратно пропорциональна скорости фильтрации или скорости скачка.
Знаменатель подынтегрального выражения в (IV.71) порядка A (s— sc), а в (IV.72) порядка А\ (s — sc)2, числитель же остается
Конечным при S
Имеем в первом случае SSXSC —С1 ехр (С/В), С, — С % в In (Sc — s), (IV.73) а во втором
S ^ sc + С2/С, С = С2/ (s — sc).
(IV.74)
|
Поэтому при |
|
Sc. |
|
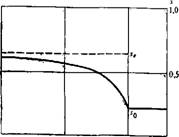
РИС. 43. Распределение насыщенности в стабилизированной зоне |
|
-1.0 |
|
-0.5 |
При s -»- so, т. е. С + знаменатель подынтегрального выражения в (IV.71) и (IV.72) имеет порядок s —so. Поэтому, если F (s) и F' (s) конечны при S = So, то имеем
С — Сі ~ Сз ln (s — s0). (IV.75)
Если F (so) = 0, то s0 < s*. Это означает, что вытесняющая фаза при С + со находится в несвязном состоянии. Рассмотрим вначале случай so = s*. Тогда, учитывая, что Ф' (s)=— /2(s)F(s)/' (s) и что при s, близких к s*, F(s)^fi (s)^ (s—s*)p, где р>1, характер функции С (s) будет зависеть от сходимости интеграла
I (Sl) = ]' (s~s^-4'(s)ds. (IV.76)
S,
Если интеграл (IV.76) сходится, то s обращается в st при конечном значении С, если же расходится, то у кривой s(С) имеется горизонтальная асимптота. Как уже отмечалось в § 1 данной главы, капиллярное давление и функция Леверетта J (s) должны быть конечными при «неподвижной» насыщенности s,, поэтому сходится интеграл §J'(s)ds и тем более интеграл (IV.76). Расходимость интеграла (IV.76) может быть лишь следствием неудачней аппроксимации эмпирических функций отнссительной проницаемости и функции Леверетта. ддимость интеграла (IV.76) при s s4 означает, что равенство s = st достигается при конечном значении координаты С = С, и при всех С > С, s остается постоянным и равным s,, т. е. существует выраженный фронт вытеснения.
Если же насыщенность So при С ->■ + со меньше st, то для всех s в интервале So < s < s, С = const, т. е. насыщенность от s0 до st меняется скачком. Возникновение скачка в решении задачи о вытеснении с учетсм капиллярных сил связано с допущением, что при насыщенностях, меньших so, еся вытесняющая фаза находится в несвязном состоянии. По-видимому, на самом деле часть этой фазы вблизи фронта становится подвижной и при насыщенностях, мень - ши х, чем s., и вблизи скачка имеется зона, где происходит обмен между связной и несвязной частями вытесняющей фазы.
Как было сказано, протяженность стабилизированной зоны обратно пропорциональна а2/ио, т. е. при использовании одной и той же среды и жидкостей обратно пропорциональна скорости вытеснения. Экспериментальная проверка этой зависимости проведена В. Н. Мартосом и В. М. Рыжиком. В экспериментах воздух вытеснялся водой при атмосферном давлении на еьіходє с постоянной скоростью из горизонтальных труб длиной 170 см, заполненных кварцевым песком с проницаемостью 10 мкм2 и пористостью 0,40. Начальная (неподвижная) водонасыщенность равнялась 0,21. Распределение водонасыщеннести по длине модели измерялось методом электросопротивления. Скорость вытеснения «о менялась в пределах 1,1 • Ю-5 — 2 • Ю-4 м/с. Во всех экспериментах и:менение водона - сыщенности со временем в различных точках по длине модели практически повторялось со сдвигом, обратно пропорциональным скорости вытеснения, т. е. образовывалась стабилизированная зона.
Протяженность стабилизированной зоны d условно определялась как расстояние между точками с насыщенностями 0,40 и 0,80. Из рис. 44 видно, что при малых скоростях (У-1 > 2 • 104 с/м)d при
близительно пропорционально V~l, как и следует из вышеуказанной теории. Однако при значении V~l около 1 • 104 с/м d(V~x) имеет минимум, а при меньших значениях V-1 снова наблюдается рост стабилизированной зоны. По-видимому, увеличение d связано с неравновесностью вытеснения, т. е. с запаздыванием перераспределения фаз в порах (см. § 4 данной главы).
Существование минимума на кривой c!(V_1) согласуется с обнаруженным ранее В. Г. Оганджанянцем наличием максимума на кривой зависимости нефтеотдачи при прорыве воды от скорости вытеснения.
Область применимости уравнения Рапопорта — Лиса ограничивается в описанных экспериментах скоростями менее 5 • Ю-5 м/с или значениями безразмерного параметра Nc
Nc = ^ < 0,7 • 10-е.
А
Такое критическое значение Nc на несколько порядков ниже критических значений Nc, необходимых для движения в порах изолированных капель, размер которых сравним с размером пор (см. § 1 данной главы). Как и аналогичный результат Д. А. Эфроса и В. П. Оноприенко о влиянии параметра Д^С = П! на нефтеотдачу, это означает, что характерные размеры систем поровых каналов, занятых каждой из фаз, и изолированных скоплений каждой фазы намного больше характерных размеров пор. Соответственно могут быть значительными и характерные времена перестройки потока под действием капиллярных сил. Возникающие при такой перестройке неравновесные явления в ходе вытеснения несмешивающихся жидкостей изучаются в § 4 настоящей главы.
Граничные условия и концевые эффекты. Рассмотрим задачу о вытеснении несмешивающихся жидкостей из образца длины L с учетом капиллярных сил в одномерной постановке, т. е. на основе уравнения Рапопорта — Лиса (IV.66), которое запишем в размерных переменных:
Ds/dt + (u0F'(s) /т) ds/dx— а2д2Ф (s) /дх2 = 0, (IV.77)
|
РИС. 45. Функция Ф (s)
|
Где
А2 = aVk/рУт, Ф (s) = — J /2 (s) F (s) J' (s) ds.
0
В тех же обозначениях из уравнений обобщенного закона Дар - си (IV. 11) и (IV. 12) следует:
U\ = uqF (s)— а2тдФ/дх, и2 = и0 — щ. (IV.78)
Типичный вид функции ®(s), соответствующей относительным проницаемостям fi (s) = s4, /2 (s) = (1 + s) (1 — s)3 и У (s) = s-1^, показан на рис. 45.
Пусть образец длины L первоначально заполнен вытесняемой жидкостью с насыщенностью а0(х) =1—So(x), и через сечение х = = 0 начинается закачка вытесняющей фазы со скоростью фильтрации и = «о (О-
Уравнение (IV.77) — квазилинейное уравнение в частных производных второго порядка параболического типа. В задаче о вытеснении для этого уравнения должны быть заданы граничные условия как во «входном» сечении при х = 0, так и в «выходном», при х = L.
Формулировка граничных условий зависит от состояния жидкостей и пористой среды вне рассматриваемого образца и от преимущественной смачиваемости его скелета вытесняющей или вытесняемой фазой, т. е. в случае вытеснения нефти водой от того, является среда гидрофильной или гидрофобной.
Заданными на входе могут быть отношение скоростей фильтрации фаз либо насыщенность, либо некоторая их комбинация. Рассмотрим некоторые типичные постановки. Пусть пористая среда соприкасается при х<0 со свободным пространством, заполненным нагнетаемой вытесняющей фазой. При этом возможны две ситуации. Если вытесняющая фаза менее смачивающая, то только она и будет двигаться в сечении, примыкающем к входному концу, т. е. будет выполняться условие равенства нулю скорости фильтрации вытесняемой фазы при дг=0, что с учетом формул (IV.78) дает
"2 =«о(1 —F (si)) + а2тдФ/дх = 0, х = О, (IV.79) где Si = s (0, t).
Если же вытесняющая фаза более смачивающая, чем вытесняемая (гидрофильная среда), то последняя может выходить в свободное пространство путем противотока. Поэтому условие (IV.79) выполняется только в том случае, если на входном конце образца установлена полупроницаемая мембрана (из материала противоположной смачиваемости), не допускающая противоточ - ной фильтрации вытесняемой фазы. Если же возможен выход несмачиваемой вытесняемой жидкости в свободное пространство, заполненное вытесняющей фазой, то такое истечение происходит в виде отдельных капель, радиус которых гр близок к радиусу самых крупных пор. В таком случае при х = 0 задается условие равенства капиллярного давления в среде капиллярному давлению в капле
Рс (si) = 2a/rpi (IV.80)
Откуда определяется значение s\ — s(0, t). Поскольку радиус гр велик по сравнению со средним радиусом пор, si оказывается близким к s* — максимально возможной насыщенности при вытеснении.
Условие (IV.79) в безразмерных переменных внешнего разложения X = x! L, х = udt/L имеет вид
1— F (Si) + ЕдФ/дхІ^о = 0, (IV.81)
Где e = a2/uoL — малая величина. При є -»- 0, т. е. в рамках нулевого приближения внешнего разложения, условие (IV.81) сводится к F (si) = 1 или si = s*.
Формулировка условия при x=L также зависит от состояния среды вне рассматриваемого образца и может быть различной. Предположим, что при х > L находится пористая среда, проницаемость которой kt много больше, чем проницаемость рассматриваемого образца, первоначально насыщенного вытесняемой фазой. На границе двух сред при двухфазном течении должно выполняться условие непрерывности давления в обеих фазах и, следовательно, непрерывности капиллярного давления. Из соотношения Леверетта (IV. 10) следует, что в высокопроницаемой среде капиллярное давление близко к нулю при всех насыщенностях, соответствующих подвижным фазам. Поэтому в основной (малопроницаемой) среде при равенстве капиллярных давлений насыщенность должна быть близка к s*, если вытесняющая фаза более смачивающая (гидрофильная среда при вытеснении нефти водой), и к s„, если она менее смачивающая (гидрофобная среда). Предельный переход оо приводит к случаю, когда при х > L происходит истечение в свободное пространство, причем выполняются граничные условия вида
S (L, 0 = s*, s (L, 0 = s,. (IV.82)
Для гидрофильной и гидрофобной сред соответственно (под s подразумевается насыщенность вытесняющей фазой).
Условия (IV.82) в отличие от (IV.81) не согласуются с условиями при x=L, вытекающими из внешнего разложения (решение Баклея — Леверетта), в котором s (L, t) = sL — переменная величина, определяемая из равенства L = uoF" (sL) t/m. Несогласованность граничных условий означает, что вблизи границы х = L образуется узкая зона (пограничный слой) с переменной насыщенностью, меняющейся от sL до st или до s*. Распределение насыщенности в этой зоне можно исследовать методом сращиваемых асимптотических разложений, вводя, как и в стабилизированной переходной зоне, «капиллярный» пространственный масштаб I = а2/ио, сохраняя, однако, масштаб времени внешнего разложения. Заметим, что при вытеснении нефти водой из гидрофильной среды начальная насыщенность So < s\ Значение s = s* при х = L достигается после подхода воды к выходному сечению не мгновенно, а через времена
порядка to = a2/u%. Значение to много меньше характерного времени вытеснения L/u0\ период установления насыщенности s* при х = L нами не рассматривается. Перейдем в уравнении (IV.77) к безразмерным переменным t = uo(L—х)/тат = = uotlm. В результате имеем
Eds/dz —F' (s) ds/dt. — д2Ф (s) /д¥ = 0.
(IV.83)
В нулевом приближении распределение насыщенности удовлетворяет стационарному уравнению
DF/dl + д2Ф/д? = 0. (IV.84)
Это означает, что ьблизи выходного сечения распределение насыщенности в ходе вытеснения квазистационарно. Граничные условия для уравнения (IV.84) определяются следующим образом: при? = 0 выполняется условие (IV.82). При X оо должно выполняться условие асимптотического сращивания с тем значением s, которое получается на границе x=L во внешнем приближении, т. е. в решении задачи Баклея—Леверетта s(—со,/) =sl(/), где Sl определяется из (IV.46) как s(L, t). Интегрируя уравнение (IV.84), получим распределение насыщенности вблизи х= L, удовлетворяющее граничным условиям при $ = 0 и $ = —оо (рис. 46).
Гидрофильная среда
S
Гидрофобная среда
Г Фг (s) ds
)F(s)-F(s)
S, L
Отклонение распределения насыщенности вблизи выходного сечения от распределения, полученного без учета капиллярности и справедливого вне концевой области, называется капиллярным концевым эффектом.
Из формул (IV.85) следует, что распределение насыщенности после полного вытеснения нефти в гидрофобной и гидрофильной пористых средах различное, т. е. в зависимости от того, какая из фаз является более смачивающей.
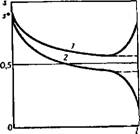
|
РИС. 46. Распределение насыщенности при вытеснении нефти водой с учетом концевых эффектов Среда: 1 — гидрофильная; 2 — гидрофобная |
Для гидрофильной среды при tоо, sL->s* амплитуда изменения насыщенности в интеграле (IV.85) стремится к нулю, и в пределе s = s* при всех х 0 < х < L, т. е. во всех точках, достигается предельная насыщенность. Если среда гидрофобна, то sL s, а нижним пределом в (IV.85) является st. Поэтому с ростом sL интеграл стремится к конечному пределу для всех s<sL. Это означает,
что после полного вытеснения, т, е. после прокачки неограниченного объема воды, в гидрофобном образце остается конечный объем нефти с насыщенностью выше н еподвижной а = 1 — S*.
|
|
Перепишем интеграл (IV.85) для гидрофобной среды в размерных переменных
(IV.86)
Формула (IV.86) описывает стационарное распределение остаточной нефти в образце. Из нее следует, что протяженность зоны концевого эффекта, т. е. зоны, содержащей остаточную нефть, обратно пропорциональна скорости вытеснения. Таким образом, конечная нефтеотдача гидрофобных сред возрастает с ростом скорости вытеснения, а нефтеотдача гидрофильных сред от скорости не зависит. Этот вывод был неоднократно подтвержден экспериментально.
Капиллярная пропитка. В неоднородных пластах возможны ситуации, когда при вытеснении несмешивающихся жидкостей влияние капиллярных сил на процесс вытеснения оказывается доминирующим. Важнейшим процессом подобного рода является капиллярная пропитка — самопроизвольное впитывание более смачивающей фазы в пористую среду, насыщенную другой фазой, без внешнего воздействия на какую-либо из жидкостей. Так обстоит дело, когда малопроницаемый блок породы, насыщенный нефтью, оказывается окруженным со всех сторон водой, продвигающейся по высокопроницаемым участкам. Тогда извлечение нефти из этого блока возможно лишь за счет капиллярной пропитки. Для получения качественных оценок рассмотрим следующий идеализированный процесс. Пусть цилиндрический образец пористой среды первоначально заполнен менее смачивающей фазой. Боковые поверхности и один из торцов предполагаются непроницаемыми, а свободный торец в начальный момент приводится в соприкосновение со смачивающей жидкостью. В результате начнется процесс противоточной капиллярной пропитки, т. е. смачивающая фаза будет впитываться, а несмачивающая выходить через единственную открытую торцевую поверхность. Очевидно, впитывание будет происходить преимущественно по мелким порам, а выход несмачивающей фазы — по крупным.
Как показывают эксперименты по противоточной пропитке, проведенные на прозрачных образцах, фильтрация обеих фаз во встречных направлениях происходит равномерно по всему сечению, и каждая из фаз движется по своей системе поровых каналов. Противоточную пропитку поэтому можно рассматривать в рамках представлений, принятых для обычной одномерной двухфазной фильтрации. Относительные проницаемости для противо - точного течения могут отличаться от соответствующих функций при однонаправленном течении обеих фаз. Однако в последующем качественном исследовании это различие не учитывается.
Уравнение закона фильтрации будем записывать в виде (IV. 10) и использовать уравнение Рапопорта — Лиса (IV.77) при условии для противоточного течения:
U0="i+"2 = 0. (IV.87)
Что дает
Ds/dt — а2д2Ф (s)/dx2 = 0. (IV.88)
Из (IV.78)
Щ = - а2т ~ = a2mf2 (s) F (s) J' (s) (IV.89)
В задаче о противоточной капиллярной пропитке граничным условием во входном сечении должно быть равенство нулю капиллярного давления, так как Рс = 0 в свободной жидкости. Иными словами, s (0, t) — s*, где s* — предельная насыщенность, при которой вытесняемая несмачивающая фаза переходит в несвязное состояние и капиллярное давление обращается в нуль. Поскольку f2 (s*) = 0, то для того, чтобы при s->s* ti] и «2 оставались КОНЄЧ-
Ds
Ными, необходимо, чтобы предел f2 (s) J' (s) ^ при X -> 0, s -> s* был
Отличен от нуля.
В закрытом сечении при х = L выполняется условие и\ == и2= 0, т. е. либо s < s,, либо ds/dx — 0. Пусть начальная насыщенность постоянна и равна So. Рассмотрим течение при временах t, удовлетворяющих неравенству
K/a2<t t « L2/a2, (IV.90)
Т. е. таких, когда распределение насыщенности в порах в тонкой зоне вблизи входного сечения (толщиной порядка размера пор) уже установилось, но возмущение не дошло до сечения х = L. Тогда s должно быть функцией только трех размерных переменных х, t и а2, из которых может быть составлена единственная безразмерная комбинация 5 = x/aVt, т. е. задача является автомодельной. Уравнение (IV.89) переходит в обыкновенное диффе ренциальное уравнение
Tds/dl + 2с12ФШ2 = 0 (IV.91)
С граничными условиями
S(0) = s*, s(oo)=s0. (IV.92)
Для s, близких к s*, Ф (s) можно приближенно представить в виде Ф (s) ~ Фд — A (s* — s)n. Тогда решение уравнения (IV.91) при условии s(0) = s* имеет для малых \ вид s* — s=CЈ2/n-1. Меняя С, можно получить семейство решений, каждому из которых соответствует свое значение s(oo) = so. Если s(0)<s*, то такое же семейство решений можно получить, меняя s' (0) (рис. 47). Искомое решение для заданного so > s. можно получить подбором такого значения свободного параметра, при котором выполняется второе краевое условие.
Обращаясь к случаю So < st, отметим, что уравнение (IV.91) при s, близких к s,, имеет вид
2A td2^/di2 + Xda/dX О, (IV.93)
Где а = s — Ф (s) Л і (s — sj", если s-+sf. Для всех реальных кривых относительной проницаемости и капиллярного давления n> 1. Как было показано в § 5 гл. II, решение уравнения вида (IV.93) достигает граничного значения а = 0 при конечном значении і = с. В данном случае это означает, что существует «фронт пропитки».
Вблизи точки X — с, о = О решение уравнения (IV.93) асимптотически представляется в виде
С~Х = 2A\ti fx"-1 (2с( + cK)~ldx. (IV.94)
О
Если s0 < s„, то на фронте пропитки, как и выше, в случае стабилизированной зоны, возникает скачок насыщенности от so до st в точке X = с. Физический смысл этого скачка тот же, что и скачка впереди стабилизированной зоны. На скачке должно выполняться условие (IV.36). Из формул (IV.89) и (IV.94) получим для и\ (? = с) выражение
Щ = (атФ' (s)/}/T) ds/dX = атс^/УТ. (IV.95)
Из условия на скачке V — ui/m(st— so) = ас/2 Vt, откуда
2 Cl=c(s, — so). (IV.96)
Тогда из (IV.94) имеем
С — 5 = 2с_| (s — sj"/(st — So), (IV.97)
С - ^ = (в1"|)с (s - s.)"-' (so = S,). (IV.98)
Соотношения (IV.97) и (IV.98) позволяют выделить из семейства интегральных кривых, удовлетворяющих условию при X — О, те, которые соответствуют заданному значению So < s,.
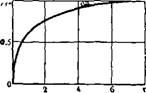
|
РИС. 48. Зависимость средней насыщенности от безразмерного времени при противоточной капиллярной пропитке
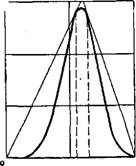
|
РИС. 47. Распределение насыщенности при противоточной капиллярной пропитке
Заметим, что при So = st вблизи Е = с «і ^ атса/2 J//, т. е. «истинная» скорость впитывающейся фазы ujmo при а - у 0 остается конечной.
В задачах двухфазной фильтрации в трещиновато-пористых средах (см. ниже) используется функция, выражающая зависимость средней насыщенности пропитывающего блока пористой среды от времени. Чтобы получить эту зависимость, следует решить задачу о пропитке образца конечной длины. Если начальная насыщенность so < s., скорость «фронта пропитки» хс конечна, то до подхода его к непроницаемой границе х = L можно использовать автомодельное решение s(Ј). При этом средняя насыщенность
І х° - s = j-\sdx = s0 + KV^ < с"2), (IV.99)
"о
Где
С
K(s°, s0) = J(s — s0)dl HV.100)
"о
Чтобы получить приближенное решение для моментов времени t > tc, воспользуемся методом интегральных соотношений. Проинтегрировав уравнение (IV.91) по х от 0 до L, получим
Й2Ф' (s°) (ds/dx)о = Lds/dt. (IV. 101)
Будем искать распределение s в виде (с учетом условия при х= L):
S = s° — 2x(2L — х) (s° — s)/3L2. (IV. 102)
Тогда из (IV. 101) получим
D's/dt = 3a2®'(s0) (s° — J)/L2. (IV. 103)
Интегрируя уравнение (IV. 103) при условии, что t=tc и решение совпадает с (IV.99), получим окончательно
S = s° — (s° — So — К/с) ехр [—ЗФ' (s°) (т — те)] (IV. 104)
При т > тс = с~2, где i = a2t/L2. Зависимость s(x), соответствующая формулам (IV.99) и (IV. 104), приведена на рис. 48.
Модель вытеснения в средах с двойной пористостью. Полученные ранее соотношения, характеризующие капиллярную пропитку, используются для построения модели вытеснения нефти водой в средах с двойной пористостью, т. е. состоящих из областей с проницаемостью k\, в которых имеются включения с проницаемостью k2<^k\. При движении вытесняющей воды по водопроницаемым зонам малопроницаемые блоки оказываются окруженными водой, и нефть из них извлекается путем противоточной капиллярной пропитки.
Ограничимся здесь только случаем трещиновато-пористых сред, общая характеристика которых приведена в § 4 гл. III, и воспользуемся гипотезами модели фильтрации в трещиновато-пористых средах (см. рис. 34). Иначе говоря, предположим, что емкость трещин намного меньше пористости блоков, а проницаемость блоков, напротив, пренебрежимо мала по сравнению с проницаемостью системы трещин. Вода движется по системе трещин, впитывается в пористые блоки, вытесняя нефть. Поступающая из блоков нефть движется далее по системе трещин.
Пренебрегая непосредственным переносом жидкости по блокам и емкостью трещин, уравнения неразрывности в каждой из систем двойной среды можно получить в виде
Div и, + q = 0, mds/dt — q = О, (IV. 105)
Где и\ — скорость фильтрации вытесняющей фазы; s — насыщенность в блоках; q — интенсивность обмена жидкостью между трещинами и блоками, определяемая скоростью капиллярной пропитки.
В принятой модели с момента подхода воды к блоку на его границе мгновенно устанавливается максимальное значение насыщенности s*, соответствующее Рс = 0. Тогда интенсивность пропитки и обмена жидкостью между фазами зависит только от времени нахождения данного элемента или блока в обводненной зоне.
В одномерном случае система (IV. 105) примет вид
Дих! дх +<7 = 0, mds/dt—q = 0. (IV. 106)
Введем, следуя Ю. П. Желтову, В. JI. Данилову и А. А. Бок - серману, неизвестную функцию t0(x)—время прохождения фронта воды в трещинах через точку с координатой х. Тогда интенсивность перетоков q в уравнениях (IV. 108) будет функцией времени нахождения блока в зоне за фронтом t—tu(x) — z. Вид функции q(z) может быть установлен, например, исходя из выражения для пропитки одного элемента (IV.104). q(т) должно быть пропорционально ds/dx, т. е.
Q = Nx(t т)-'/2, т < тс;
(IV 107)
Q = (N2а2/L2) exp (— WO, х > %с, К '
Где N\, N2 и X — постоянные.
Выражение (IV.107) получено из приближэнной формулы (IV.104). Болег удобно использовать для q (т) единую аппроксимацию для всех т, например, предложенную Э. В. Скворцовым, формулу
= (IV. 108)
Постоянные А и b подбираются так, чтобы ближе соответствовать формулам (IV. 107) или экспериментальным данным.
Рассмотрим одномерную задачу вытеснения нефти водой из трещиновато-пористой среды для модели, описываемой системой (IV.106). Проинтегрируем первое из этих уравнений от х = 0 до фронта воды х =Хо (t) = /(/).
(0 ~^q[t-T [x)\dx = \q(t-T)f (Г) dT. (IV. 109)
Если задана скорость вытеснения при х = 0 U\ (t), то, решая интегральное уравнение (IV. 109), можно найти скорость продвижения фронта f (t) и обратную функцию to(x).
Тогда из второго уравнения системы (IV. 106) найдется распределение насыщенности в блоках
S-So=y~fX)q(z)dx. (IV.110)
О
Правая часть уравнения (IV. 109) имеет вид свертки, и оно может быть решено методом преобразования Лапласа. Пусть U (к), Q (X) и *F(X)— преобразования Лапласа функций ux(t), q(t) и f{t) соответственно. Тогда из (IV. 109) получим, пользуясь теоремой о свертке и условием / (0) = 0,
ЩХ) = U (X)/XQ (к). (IV. 111)
Пусть <7(0 Еыргжается формулой (IV.1C8) и и —-■ и0 = const Тогда
F (X) = w01/Т+Ь/А (IV. 112)
В результате по таблицам преобразования Лапласа можно найти
/ (/) = (uo/A Уъ) (1 + 2bt) erf (УЫ) + (2«о/А У^ГЬ) (1 + е-*'),
(IV. 113)
/' (0 = (2«0 УЫА Уъ) erf (УЫ). (IV. 114)
Из формулы (IV. 114) следует, что при со скорость перемещения фронта
V = 2и0\, ЇЇАУк. (IV.115)
Если /'(t) = V = const, то в соответствии с формулой (IV. 110) получим
S = So + (s° — So) erf (Уъ (t — x/V)). (IV. 116)
Таким образом, s есть функция х—Vt, т. е. при оо распределение насыщенности приобретает вид бегущей волны.
Все изменение насыщенности ОТ So до s° происходит в зоне, перемещающейся с постоянной скоростью, протяженность которой имеет порядок uol2/a2. Эта зона по аналогии с рассмотренной выше зоной вблизи скачка при обычном вытеснении получила название стабилизир ованной. Однако в отличие от зоны, описываемой уравнениями (IV.71) или (IV.72), протяженность стабилизированной зоны пропорциональна ио, а не ыо"1. Для трещиновато-пористой среды капиллярные силы оказывают стабилизирующее влияние на процесс вытеснения. В случае однородной среды капиллярные силы вызывают диссипацию («размазывание») фронта вытеснения (см. § 4 данной главы).