ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ

Структура двухфазного течения при крупномасштабном описании. Задача Баклея-Леверетта

На вытеснении нефти водой или газом основана технология ее извлечения из недр при разработке нефтяных месторождений. Это либо вторжение в пласт краевой воды или газа газовой шапки, продвигающих нефть к забоям добывающих скважин (естествен­ный напорный режим), либо закачка вытесняющей жидкости или газа через систему нагнетательных скважин для поддержания дав­ления в пласте и продвижения нефти к добывающим скважинам. Рассмотрим задачу о вытеснении нефти водой или газом (более широко — задачу о вытеснении одной несмешивающейся жидкости другой) на основе уравнений двухфазной фильтрации, полученных в предыдущем параграфе. Для решения системы уравнений (IV.11) — (IV. 15) широко применяется аппарат численных мето­дов. Основываясь на общих принципах, изложенных в гл. I, огра­ничимся только исследованием общих свойств поля насыщенности, для чего применим асимптотический подход, основанный на малос­ти некоторых безразмерных параметров, входящих в условия зада­чи о вытеснении несмешивающихся жидкостей [5].

Уравнения Баклея — Леверетта. Общая теория. Запишем основную систему уравнений для давления и насыщен­ности в виде (IV.19) и (IV.20), используя безразмерные пере­менные

X = x/L, Y = y/L, Z = z/L, х = kkpt/mpiL = = uot/mL, Pi = pjAp, П = P/Ap, є = a2/u0L = = a cos 6 Y~kl V mAp.

Здесь L — характерный размер (например, расстояние между скважинами или галереями); «о —характерная скорость, связанная с характерным перепадом давления Ар. Получим

Div [<р (s) grad П] = 0, (IV.27)

Ds/dt — div [fі (s) grad П] — єДФ (s) = 0, (IV.28)

Где Д — оператор Лапласа.

В задачах нефтяной подземной гидродинамики перепад давления на границах области течения, размер которой достигает сотен мет­ров, составляет несколько десятых или единиц мегапаскалей, скорость фильтрации Ю-6—Ю-5 м/с, капиллярное давление в неф­тяных пластах равно Ю-4—Ю-2 МПа, а параметр а2—Ю-8 — — 10~6 м2/с. Отсюда следует, что параметр є в уравнении (IV.28) порядка Ю-2—Ю-4, поэтому в крупномасштабном приближении членом, содержащим є, можно пренебречь, т. е. записать вместо (IV.28)

Ds/dt — div [/і (s) grad П] = 0. (IV.29)

Чтобы исследовать общие свойства поля насыщенности на основ уравнений (IV.27) и (IV.29), последние удобнее переписать в раз­мерном виде

Div и — 0; и = — {kf (s)/[i. i) gradр, (IV.30)

Mds/dt + F' (s) (и grad s) = 0, (IV.31)

Где » = U\ + «2 — суммарная скорость фильтрации обеих фаз. Си­стема уравнений (IV.27) и (IV.29) эллиптического типа относитель­но давления и гиперболического — относительно насыщенности. Для уравнения (IV.31) можно получить семейство характеристик, на котором выполняются соотношения

Dx/dt = uF' (s)/m, dy/dt = vF' (s)/m, (I V.32)

Dz/dt = wF' (s) /m, ds/dt = 0.

Соотношения (IV.32) при заданном мгновенном поле скоростей можно рассматривать как уравнения распространения точек с по­стоянной насыщенностью. Рассмотрим поверхность Г с постоянным на ней значением насыщенности s (так называемую изосату), урав­нение которой ф (х, у, z, t) = 0. Тогда из (IV.32) следует

Vn = (d^/dt)(d^/dn) = unF' (s)/m, (IV.33)

Где Vn — скорость перемещения изосаты по нормали к ней; ип — проекция суммарной скорости фильтрации на нормаль к изосате.

В задаче о вытеснении несмешивающихся жидкостей в систе­ме скважин или галерей граничными условиями для уравнений (IV. 30) и (IV. 31) являются, во-первых, обычные условия для давления, задаваемые на скважинах или галереях при движении несжимаемых жидкостей (см. гл. II), и, во-вторых, условия для насыщенности на нагнетательных скважинах или галереях. Когда нагнетается чистая вытесняющая фаза, насыщенность на конту­рах нагнетания должна, очевидно равняться максимальной s*. Кроме того, для насыщенности должно быть задано начальное распределение s(x, у, г, 0) =f (х, у, г).

Уравнения (IV.32) означают, что при заданной скорости фильтра­ции скорость распространения насыщенности s пропорциональна производной функции Баклея — Леверетта F'(s). Типичные кривые относительной проницаемости как для смачивающей, так и для не - смачивающей фазы вогнуты к оси s, вследствие чего функция F(s), равная тождественно нулю при s < s* и единице при s > s*, имеет точку перегиба, а функция F'(s)—максимум (см. рис. 37). Поэтому в соответствии с формулами (IV.32) большие значения насыщенности вытесняющей фазой s (на рис. 38 слева) могут «обгонять» меньшие (на рис. 38, начиная с Т = 0,5), вследствие чего появляются поверх­ности разрыва (скачки), при переходе через которые насыщенность меняется на конечную величину.

Появление скачков насыщенности связано с пренебрежением членом со старшей производной в уравнении (IV.28). Скачками насыщенности аппроксимируются области, внутри которых велик |grad s|, и поэтому нельзя пренебрегать последним членом урав­нения (IV.28). При точном решении (IV.28) вместо скачков воз­никают узкие области с быстро меняющейся насыщенностью. Асимптотическому исследованию распределения насыщенности в этих зонах посвящен следующий параграф.

Прежде чем исследовать формирование и эволюцию скачков насыщенности, выведем соотношения, выражающие условия со­хранения массы и давления на них.

Пусть скачок насыщенности проходит через цилиндрический эле­мент пористой среды объемом 2, вырезанный по нормали к поверх­ности скачка и ограниченный участками поверхностей S, параллельных поверхности скачка, находящихся на расстоянии Дп от нее. Условие сохранения массы первой фазы в элементе имеет вид

D ||msdwj /dt + I u\ndo = 0. ^jy 34^

Далее

D (J msdu)/dt=mVnc(s--s+) £ + 0 (S/i?2), (IV.35)

Где s~, s+ — соответственно насыщенности за и до скачка; R — радиус кривизны поверхности скачка; Vnc — скорость перемещения скачка по нормали к нему. Разность потоков вытесняющей жидкости через сечения, параллельные поверхности скачка, равна (мПі — где,

U\n — проекция скорости фильтрации первой фазы на нормаль к по­верхности скачка. Поток, связанный с касательной составляющей, исчезающе мал при стремлении Дп к нулю. Тогда условие сохране­ния массы первой жидкости при стягивании элемента 2 к участку поверхности примет вид

Vnc=(urn-utn)/m(s--s+). (IV. 36)

Условие сохранения массы второй жидкости с учетом (IV. 36) сводится к условию непрерывности нормальной составляющей сум­марной скорости фильтрации при переходе через поверхность раз­рыва:

Ч\п + "2 п — U„ = lit = Un.

Из (IV.30) и (IV. 17) нетрудно полу­чить

Щ = F(S) и, Из = (1 — F(S)) и. (IV.37)

Эти формулы показывают, что по физическому смыслу функция Бак - лея— Леверетта F(s) выражает долю первой фазы в потоке (при пренебре­жении капиллярными силами). Под­ставляя их в (IV.36), имеем

Vnc = [F(s~) — F (s+)] Un/m (s - — s+). (IV.38)

Кроме условий (IV.36) на скачке должно выполняться условие непрерывности давления, которое сводится к следующим соотно­шениям:

(<Зр/дЪ)- = (др/дЬ)+; иъ/и= ср (s+) /ср (s ), (IV.39)

Где & — направление по касательной к поверхности скачка; ы» — проекция скорости фильтрации на это направление. Различие каса­тельных и сохранение нормальных компонент скорости фильтрации приводит к излому линий тока при переходе через скачок.

Рассмотрим подробнее возникновение и распространение скач­ка в одномерном случае, когда вместо уравнений (IV. 30) и (IV. 31) имеем

Mds/dt + uF' (s) ds/dx = 0; и = и (t). (IV.40)

Пусть начальное распределение насыщенности монотонно s0 (х)<0. Из (IV.32) получим решение уравнения (IV.40) в виде

T

Х = x0(s) + UF'(s)/m; U = lu(x)dx. (IV.41)

О

Поскольку функция F'(s) имеет максимум, формальное решение (IV.41) при достаточно больших временах становится неоднозначным, фактически же в момент когда касательная к кривой s (х, определяемой формулой (IV.41), становится вертикальной, возникает скачок насыщенности. Из формулы (IV.41), записанной для насыщен­ности на скачке s~ = sc, получим, дифференцируя по t:

Dxjdt = [uF'(sc)]/m + [UF'(sc) + x'0 (sc)] dsjdt. (IV.42)

Далее, приравнивая (IV.42) выражению для скорости скачка (IV.38), получим дифференциальное уравнение для насыщенности на скачке sc:

Dsc/dt = и [F(sc) - F(s0) — F'(se) (sc — so)]/ (sc - s0) [UF"(sc) +

+ mx'0(sc). (IV.43)

Чтобы определить значение So = s+, входящее в уравнение (IV.43), нужно использовать условие x (sc) = л; (so) или

UF'(sc) + тхо (se) = UF'(so) + тх0 (s0). (IV.44)

Из уравнения (IV.43) следует, что если насыщенность на скачке при его распространении остается неизменной, то она должна удов­летворять соотношению

F'(se) = [F(se) - F(s0)] / (se - so), (IV.45)

Впервые полученному Баклеем и Левереттом. Оно означает, что ско­рость распространения стационарного скачка равна скорости рас­пространения насыщенности на скачке — см. (IV.33) и (IV.38). Урав­нение (IV.43) для sc = s~ получено С. И. Бузиновым И. А. Чарным.

Условие (IV.45) допускает простую геометрическую интерпрета­цию на плоскости переменных F, s: значение sc находится как точка
касания прямой АВ, проведенной из точки s = so, к кривой F(s) (рис. 39). При этом тангенс угла наклона прямой АВ к оси s про­порционален скорости скачка.

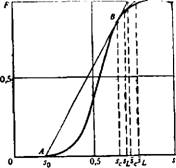
Если начальная насыщенность s0 постоянна, а во входном сече­нии х = 0 выполняется условие s (0, t) = s*, то распределение на­сыщенности описывается классическим решением Баклея — Леверетта

X=UF'(s)/m, (s*>s>sc), x=UF'(sc)/m, (s0<s<sc),

S = s0 при mxjU > F'(sc), (IV.46)

В котором насыщенность на скачке постоянна и удовлетворяет условию (IV.45) при s0 == const (рис. 40).

Выше рассмотрены задачи о вытеснении для плоскопараллельного одномерного течения. Однако нетрудно показать, что решения (IV.41) и (IV.46) описывают также плоско-радиальное и сферически - радиальное течение лишь с заменой координаты х на г2/2 и г3/3 соответственно. Для стационарного цилиндрического или сферическо­го скачка остается справедливым и условие Баклея — Леверетта (IV.45)

Для общего пространственного движения выражение (IV.38) можно использовать для описания эволюции поверхности скачка <\>с (х, у, z, t), поскольку

У по = Щс№)\Щс! дп). (IV.47)

Пусть в некоторый начальный момент вдоль поверхности скачка насыщенность постоянна и выполняется условие (IV.45). Пусть, кроме того, везде за скачком (т. е. со стороны контуров нагнетания) s > sc, F'(s) < F'(sc), т. е. насыщенности за скачком в его окрестности не «обгоняют» насыщенность на скачке в соответствии с условиями (IV.32) и (IV.33), а насыщенность sq постоянна. Тогда, очевидно, скачок и изосата s = sc будут распространяться совместно, т. е. усло­вие (IV.45) будет выполняться в течение конечного промежутка времени. В частности, если начальная насыщенность постоянна,

А на нагнетательных скважинах равна s*, то в окрестности сква­жин в начале вытеснения осуществляется решение Баклея — Ле - веретта для плоско-радиального течения. В таком случае на об­разующихся скачках (фронтах вытеснения) насыщенность опре­деляется по соотношению (IV.45) и в дальнейшем при искривле­нии поверхности скачка продолжает оставаться постоянной и равной sc. Выполнимость условия Баклея — Леверетта в общем случае плоского вытеснения была отмечена Г. П. Цыбульским.

Частные случаи. Рассмотрим некоторые частные случаи одномерной задачи вытеснения и следствия из формул Баклея — Леверетта.

Образование скачков насыщенности связано с существованием интервалов изменения s, на которых функция F(s) имеет вогнутую форму. В зависимости от вида кривых относительной проница­емости и отношения вязкостей возможно как отсутствие таких ин­тервалов и, следовательно, скачков насыщенности, так и образова­ние нескольких скачков. Рассмотрим случай, когда относительные проницаемости могут считаться пропорциональными соответствую­щим насыщенностям, т. е. fi = s, /г=1 — s. Такими функциями можно описать совместное течение взаимно смешивающихся жидкостей, когда распределение фаз в порах полностью слу­чайно и не связано с капиллярными силами, причем каждая из фаз сохраняет подвижность при любой насыщенности. Тогда

F(s) = s/[(jl0 + (1 — но) s], F'(s) = !W[u0 + (1 - но) s]2,

F"(s) = - 2ja0 (1 - но) / [Но + (1 ~ Ho) s]3. (IV.48)

Из (IV.48) следует, что функция F"(s) сохраняет знак при любых s, причем, если но < 1, то F"(s) < 0, и обратно: если ио>1, то F"(s)>0. В первом из этих случаев по формуле (IV.37) получаем непрерывную монотонно убывающую зависимость s(x) при любом t. Вид решения Баклея — Леверетта при условии, что функция F(s) выражается фор­мулой (IV.48) и но = 0,5, показан на рис.40 вместе с решением Баклея — Леверетта для обычных функций относительной проница­емости. Если ро^О, производная F"(s) нигде не отрицательна. Вследствие этого непрерывное решение, соответствующее (IV.37), не существует. Решение со скачком соответствует предельному случаю «поршневого» вытеснения:

S = 1 (* < Um); s = So (х > Um). (IV.49)

Физически это означает, что если вязкость вытесняющей фазы больше, чем вытесняемой, процесс вытеснения имеет поршневой характер. Если же больше вязкость вытесняемой фазы, фронт вытес­нения «размывается». Качественное различие вида решения при зна­чениях параметра но, больших и меньших единицы, связано с вопросом об устойчивости фронта вытеснения, рассматриваемым в § 5 настоя­щей главы. Решения уравнения (IV.40) с функцией F(s) вида (IV.48) рассматривались А. М. Пирвердяном в связи с задачей о перемещении водонефтяного контакта.

Одной из практически важных характеристик вытеснения нефти водой является коэффициент нефтеотдачи, т. е. доля вытесненной нефти от первоначального ее содержания в пористой среде. Из авто­модельных решений вида (IV.46) можно получить простые соотно­шения, позволяющие оценить зависимость коэффициента нефтеотдачи от объема прокачанной жидкости и отношения вязкостей фаз. Пусть вытеснение происходит из элемента трубки тока между сечениями л: = 0 и х= L при s(x, 0) = so = const. Поскольку условия в выход­ном сечении л = L не влияют на решение задачи Баклея — Леверетта, формулы (IV.46) справедливы для образца конечной длины L, причем насыщенность в выходном сечении находится по формулам (IV.42) или (IV.46) как s(L, t).

Пусть насыщенность в выходном сечении х = L, sL равна или больше насыщенности на скачке sc, определяемой формулой (IV.45), т. е. рассматриваются моменты времени после прорыва вытесняющей жидкости через выходное сечение. Для насыщенности при х = L, s = Sl выполняется равенство

F'(sl) = LIU т. (IV.50)

Средняя насыщенность в рассматриваемом участке с учетом (IV.46) равна

L SL

S = L~x £ sdx = (F'(sl))-1 f sF''(s) ds = sL + ( 1 - F(s)) /F'(sL) -

О s*

— S*F'(s*)/F'(Sl). (IV.51)

Обычно вид функций /і (s) и /2 (s) таков, что f2 (s*) = 0 и f\ (s#) = 0, откуда и F'(s*) = 0. Тогда, по Уэлджу, связь между s и sL примет вид l=sL+(l-F (sL)) /F'(Sl). _ (IV.52)

Отсюда следует, что при заданном sL значение s можно найти с помощью простого построения на плоскости F, s, указанного на рис. 39. В частности, средняя насыщенность при прорыве вытесняющей фазы находится на пересечении касательной к F(s) из точки so, F(sq) (дающей значение sc) с прямой F = 1. Зная s, нетрудно найти коэф­фициент нефтеотдачи т] и обратно:

Т, = (7— s0)/(l — so); s= (1 — so) та + s0. (IV.53)

Кроме определения коэффициента нефтеотдачи, формулы (IV.51) и (IV.52) можно использовать для нахождения вида функции F (s) по экспериментальным данным, полученным при вытеснении нефти водой. Измеряя расходы нефти и воды q2 и q\ в каждый момент времени, можно найти по ним текущее значение функции F, соответ­ствующее насыщенности в выходном сечении Sl : F(sL) = q\/(qi + q2). Далее, по текущей нефтеотдаче можно найти значение s в любой момент времени. После этого значение sL, соответствующее данному F, можно определить по формуле (IV.51) с учетом (IV.50):

St = s— Um{\— F)/L. (IV.54)

На основе автомодельного решения Баклея—Леверетта, Д. А.Эф­рос [48] и ряд других исследователей предложили формулы, позво - 134 ляющие определить по данным вытеснения нефти водой в линейном образце не только функцию/7^), но и относительные проницаемости. Для линейного вытеснения после прорыва вытесняющей фазы перепад давления Др можно выразить формулой, следующей из (IV.41):

К

Др = JX, uoUmk-« J F"(s)lfi (s) + |»o/2(s)]-'ds. (IV.55)

S*

Заменив в соотношении (IV.55) переменную s на F' = dF/ds, получим

F'l

J (F/f\) dF' = Дp (t) kF'L/uo (t) p\L, F'l = F'(sl). (IV.56) о

Полагая kkp/u0 (t) pjL = П

И дифференцируя соотношение (IV.56) no U = itiL/Fl, найдем для /і (sl):

H (sl) = F/IU. - U (dH/dU)]. (IV.57)

Все величины, входящие в правую часть (IV.57), можно вычис­лить по результатам измерений интегральных характеристик про­цесса вытеснения и перепада давления.

Схемой Баклея — Леверетта можно описать также одномер­ное двухфазное течение с учетом силы тяжести. В крупномасштаб­ном приближении, т. е. в области, где можно пренебречь влиянием капиллярных сил, выражение закона фильтрации двухфазной жид­кости с учетом силы тяжести имеет вид:

«і = — (kfi (s)/[M)d(/>+ pigsina)/d.*, и2 = — (kf2 (s) / |a2) д (p + p2g sin a)/dx. (IV.58)

При этом ось x направлена вверх, 0 < a <

Уравнения неразрывности сохраняют для прямолинейного тече­ния вид

Mds/dt + диі/дх = О, щ + и2 = и (t). (IV.59)

Простые преобразования приводят к одному уравнению для s, если и {t) задано:

Mds/dt + udF (s)/dx — Wd [f2 (s) F (s)] Idx = 0, (IV.60) где W = (kglp.2) (pi — p2) sin a, щ = uF (s)—Wf2(s)F (s).

Решение уравнения (IV.60) определяется интегрированием систе­мы уравнений характеристик

Dx/dt = и (t) F' (s) — Wdf2F/ds; s = const. (IV.61)

Если характеристики, определяемые уравнениями (IV.61), пере­секаются на плоскости х, t, для отыскания решения, имеющего физический смысл, нужно вводить скачки насыщенности. Условия
на скачках снова выражаются формулами (IV.36) и (IV.38), где вместо F (s) следует подставить функцию ф (s, t) = uF — Wf2 F.

Особый интерес представляет течение при условии и (t) = О, что соответствует разделению фаз под действием силы тяжести (грави­тационная сегрегация). Если пласт неограничен по толщине, а жидко­сти вначале разделены резкой горизонтальной границей, причем более тяжелая жидкость находится сверху, т. е. s = I при х > 0, s = О при х < 0, решение уравнения (IV.60) при и = 0 может быть запи­сано в виде

6 = xm/Wt = - d (№) Ids. (IV.62)

Функция §{s) ~f2F, типичный вид которой изображен на рис. 41, имеет две точки перегиба, что вызывает возникновение двух скачков, на которых должно выполняться условие

Dxjdt = = [ф (Sc) — ф (so)] / (sc — s0). (IV.63)

Для стационарного скачка должно выполняться условие, анало­гичное (IV. 19):

Ф' (Sc) = [ф (Sc) - ф (So)] / (s, - So). (IV.64)

Согласно этому условию, насыщенности sci и sc2 находятся с по­мощью графического построения на плоскости ф, s, показанного на рис. 41. Соответствующая картина распространения скачков на плос­кости s, £ показана на рис. 42.

Предлагаем читателю самостоятельно исследовать движение, воз­никающее, когда при всех х > 0 s (0, t) = si = const, s* < Si < s*, граница x — 0 непроницаема, что соответствует сегрегации равномер­но распределенных фаз.