ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Стационарные задачи фильтрации неньютоновских жидкостей
Из сказанного в § 1 данной главы следует, что основная особенность движения неньютоновских жидкостей в пористой среде —■ нелинейность закона фильтрации. Для структурирующихся систем это типичная псевдопластическая нелинейность, при которой подвижность увеличивается с увеличением скорости фильтрации; качественная модель и крайнее выражение ее соответствуют закону фильтрации с предельным градиентом (III. 9). Поэтому подземная гидродинамика неньютоновских жидкостей это прежде всего теория движений, не следующих закону Дарси.
В этом параграфе кратко изложены подходы и результаты теории стационарной фильтрации неньютоновских жидкостей; в следующем сделано то же применительно к неустановившимся движениям.
Основные уравнения и общие утверждения. Уравнение нелинейного закона фильтрации несжимаемой жидкости в изотропной пористой среде можно представить в виде [43]
Vfl" = — Ф(ш) w/w; Ф(0) = X > 0, Ф'(да) > 0, 0 < w< оо. (III. 10)
Если X > 0, то имеется предельный градиент давления и подразумевается, что при I v# | < х движение отсутствует (да = 0); если X = О, движение происходит при любом перепаде напора.
Уравнение (II1.10) вместе с уравнением неразрывности
VW = 0 (III.11)
Образует систему уравнений фильтрации неньютоновских жидкостей. Граничные условия для этой системы формулируются так же, как в обычных задачах стационарной фильтрации, следующей закону Дарси (см. § 1, гл. II).
Поскольку система (III. 10) — (III. 11) нелинейна и функция Ф может иметь различный вид для различных систем жидкость — пористая среда, основная цель исследования заключается в отыскании достаточно общих подходов и фактов. Для фильтрационных течений неньютоновских жидкостей сохраняют силу основные качественные свойства напорных фильтрационных течений, сформулированные в § 2 гл. II.
Рассмотрим течение в неоднородной среде и будем полагать, что неоднородность среды полностью характеризуется зависимостью от координат параметра р = р (х, у, г), называемого далее параметром сопротивления. Этот параметр — дополнительный аргумент в уравнении закона фильтрации.
Обозначим
H = v//, h = \h\, h = Ф (w, р), w = ЧГ (h, р), Ф, р > 0, f, f<0
(III.12)
И введем функции
W h
D(w) = f Ф (да, p)dw, R (h) = С W (h, P) dh, (III.13)
О "o
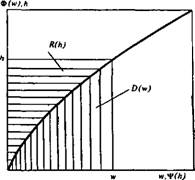
Называемые далее потенциалом диссипации и дополнительным потенциалом диссипации. На рис. 21 им соответствуют заштрихованные площади под кривой Ф (w) и слева от нее. Если ввести полные потенциалы для области V соотношениями
D'[w]^4D{w, р)dV, R'lh] = $R(h, ?)dV, (111.14)
V
|
РИС. 21. К определению потенциала диссипации и дополнительного потенциала диссипации
|
То для них будут справедливы все утверждения, приведенные в § 2,гл. II. Используя это обстоятельство, удается показать единственность поля скоростей и (при отсутствии предельного градиента давления) поля напоров в задачах с обычными краевыми
условиями и доказать принцип максимума в несколько измененной форме: напор принимает свои максимальное и минимальное значения на границе области течения. Здесь под областью течения понимается та часть V+ рассматриваемой области V, в которой до>0, включая границу (т. е. замыкание V+ области Если предельный градиент давления отсутствует, то V+=V, и это соответствует обычной формулировке принципа максимума, при предельном градиенте, не равном нулю, различие формулировок существенно (см. пример, с. 148).
Наибольший интерес, как и в линейном случае, представляют оценки для расхода фильтрационного потока через обобщенную трубку тока. Пусть На — заданный перепад напора на трубке тока, Q — отвечающий ей расход. Функции
Q = S(H0), Но = Z(Q) (III. 15)
Назовем расходными характеристиками трубки тока. На решениях задачи функционалы D* и R' превращаются в функции одного аргумента, в качестве которого мы будем брать, соответственно, Q и Но. Имеем следующие основные формулы: dD' И о dR<[H] dQ - Щ--Ч' (Ш-16)
D-(Q) + R'(Ho) = QHO. (III. 17)
Назовем
Q = Ho'R*(Ho)-, Ho = Q~'D'(Q) (III.18)
Сглаженным расходом и сглаженным напором соответственно.
Из сказанного следует, что для сглаженного напора при фиксированном расходе и для сглаженного расхода при фиксированном напоре справедливы все утверждения § 2, гл. II. Для степенного закона фильтрации удается получить оценки непосредственно для расхода и перепада давления.
Действительно, в этом случае
Ф (w, р) = Рw\ W (h, р) = (Л/р)'/5,
S+1
D[w) = T^rw'+\ Ям = г+Т(Л/Р) ' • (ШЛ9)
Тогда, если w и Н — решение, то с учетом (III.16) имеем
SD (w) = R (h); D'[w] = s-lR-[H] = (\ +s)~xQH0, (II1.20)
Откуда
Q = (s+ l)s-'Q; H0 l)H0. (111.21)
Таким образом, поскольку при степенном законе фильтрации расход и напор пропорциональны соответственно сглаженным расходу и напору, для них верны все утверждения § 2, гл. II.
Для произвольного закона фильтрации справедливы следующие утверждения [17].
A. Принцип вдавливания. При вдавливании внутрь области фильтрации входной поверхности расход и скорости фильтрации во всех точках выходной поверхности не уменьшаются (при фиксированном перепаде напора).
Для двумерного случая доказано двойственное утверждение: при вдавливании внутрь области непроницаемых границ трубки тока расход не увеличивается.
B. Если для данного закона фильтрации Ф(пу, р), р(х, г/, z) справедливы неравенства
= < ф (w, р) или Ф (w, р) < (II 1.22)
(р(- >0, Si > 0 — постоянные), то для соответствующих расходов Qi>Q> Q2-
C. Если
K
Ф(ш, р) > £ hpiWi, h = const, (111.23)
»=i
То при фиксированном Q
Ho>%hHQl. (III.24)
Здесь Ноі — перепад напора при течении с расходом Q в области той же формы при степенном законе фильтрации вида
Ф (w, р) = РiW4.
D. Если
¥ (h, р) < £ 7<рГ1А'Л, Ті > 0, (111.25)
£=1
То при фиксированном Н0
Q>ST'Q'. ("1-26)
I=i
Здесь Qi — расход фильтрационного потока через данную область при том же перепаде напора Н0 для закона фильтрации вида Ф = piWH.
Ниже приведены примеры использования этих общих утверждений.
Плоская задача. Рассмотрим плоскую задачу теории фильтрации при нелинейном законе сопротивления в однородной и изотропной среде. Введем обычным образом функцию тока •ф (х, у), после чего система уравнений, описывающих движение, может быть представлена в виде
Я, * = — Ф (w) u/w, ф, * = — v,
Н, у = — Ф (а») v/w, ([».„ = «, (II 1.27)
U = O>COS0, f = ш sin 6.
Здесь w — модуль скорости фильтрации; 0 — угол, составляемый ею с положительным направлением оси х. Система уравне-
ний плоской задачи (III.27) превращается в линейную если за неизвестные величины взять і|з и Н, а за независимые переменные w и 8. Это линеаризующее преобразование годографа было с успехом использовано в газовой динамике С. А. Чаплыгиным. Возможность его применения в теории фильтрации следует из установленной С. А. Христиановичем [43] аналогии между уравнениями фильтрации при нелинейном законе сопротивления и газовой динамики.
После несложных выкладок получим
|
(II 1.29) |
Дн Ф2 дф. дН Ф дф
Да w<S>'(w) ди>' dw дв'
Dy — '^dH + ^d*.
Соотношения (III.29) позеоляют, найдя решение системы (111.28), определить х и у как функции w и 6. Тем самым установлена связь между координатами х и у и напором Н и функцией тока ф, Еыраженная через параметры шиб.
Основная система уравнений (III.28) — однородная линейная система эллиптического типа, которую при желании можно свести к одному уравнению для напора или функции тока:
+ = (ІІІ. ЗО)
Dw \шФ(w) dwj w db
R(if)+W'VW) ~~y — 0- (III.31)
Ды>\Ф dwI 1 ф2(ш) a02 v '
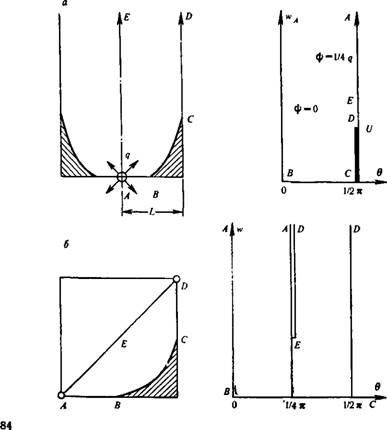
Эффективность решения конкретной задачи зависит от того, какая именно краевая задача для уравнений (ІІІ. ЗО) — (III.31) должна быть решена на плоскости годографа (w, 0). Характер этой краевой задачи определяется, в основном, геометрией области движения в физической плоскости {х, у). В тех случаях, когда область движения — многоугольник, стороны которого либо непроницаемые границы, либо линии постоянного напора, на всех них направление скорости фильтрации постоянно на каждом участке и задано заранее (соответственно, вдоль границы или перпендикулярно к ней), так что граница области в плоскости годографа состоит из отрезков линий 6= const. Если в области движения имеются источники или стоки, то в плоскости (w, 0) им отвечает бесконечно удаленная точка ш-»-оо, 0<9<2я. При отличном от нуля предельном градиенте давления в области фильтрации могут образоваться зоны, в которых скорость фильтрации равна нулю («застойные зоны») и область течения оказывается областью с неизвестной границей (рис. 22), Поскольку на границе застойной зоны скорость фильтрации w обращается в нуль, этой неизвестной границе в плоскости годографа соответствует отрезок линии w = 0
(под углом 0 при этом естественно понимать направление не обращающегося в нуль вектора градиента напора VН; оно совпадает с направлением касательной к границе застойной зоны). Таким образом, в задачах фильтрации с предельным градиентом преобразование годографа не только позволяет преобразовать нелинейную задачу в линейную, но и область с неизвестной границей застойной зоны переводит в известную область плоскости годографа.
Во всех случаях показанная на рис. 22 область в плоскости годографа отвечает элементу симметрии области течения; соответствие точек показано буквами, а граничные условия задачи в плоскости годографа указаны на рисунках. Заметим, что при анализе течений с предельным градиентом удобно считать, в отличие от общепринятого, w и 0 декартовыми (а не полярными) координатами в плоскости годографа. Вызвано это тем, что асимптотика решения вблизи линии w = 0 нетривиальным образом свя-
|
РИС. 22. Примеры отображения области течения на плоскость годографа. Расстановка скважин: А — рядная цепочка скважин: б — площадная (элемент пятиточечной системы площадного заводнения)
|
З-ана со структурой течения и ее можно задавать по-разному.
После сведения задачи при помощи преобразования годографа к линейной эллиптической задаче в известной области решение ее оказывается делом математической техники, хотя порой и достаточно сложной. Отсылая интересующихся этой, сейчас уже достаточно разработанной, стороной дела к книге [9], рассмотрим некоторые простые решения.
Как обычно в гидродинамике, для качественного анализа принципиальное значение имеет исследование асимптотики решения вблизи особых точек потока. Такими точками являются, прежде всего, окрестности источников и стоков (скважин), где скорость потока обращается в бесконечность, окрестность бесконечно удаленной точки, в которой скорость стремится к нулю, окрестность критической точки потока (при фильтрации с предельным градиентом давления — застойной зоны), где скорость потока обращается в нуль, и окрестность угловых точек границы потока.
Рассмотрим течение вблизи скважины. Окружим ее линией Г2, на которой модуль скорости имеет некоторое постоянное значение w =2 и которая целиком расположена внутри области движения. На плоскости годографа области внутри этой линии отвечает полуполоса П2:
2 < w < со, О < 8 < 2r, (III.32)
В которой искомое решение задачи для функции тока ф (w, 6) удовлетворяет уравнению (III.30) с условиями
Ф (0) = 0, ф(2*) = q, ф(2, 9) = /(9), /(0) = 0, f(2n) = q, (111.33)
Ф (оо, 0) < М < ОО.
Здесь q — интенсивность источника; /(9) — неопределенная функция, характеризующая распределение потока вдоль линии Г2. Последнее условие означает, что функция тока вблизи особой точки ограничена и мы имеем дело именно с источником (а не с комбинацией источника и диполя).
Если считать функцию f (9) известной, решение в области П2 легко получить методом Фурье, поскольку независимо от вида закона фильтрации уравнение (II 1.31) не содержит в явном виде угловой переменной 9. Нетрудно убедиться обычными методами, что в данном случае имеем
Ф(до, 9)= £ РпП (w) sin ^ , до >2, (III.34)
Я = 1
Где Рп/2 (до) — убывающее на бесконечности решение обыкновенного линейного дифференциального уравнения
|
Ф' Р - |
|
ШФ' (w)' |
F.2
/2-^ = 0, / = 4- П. (II 1.35)
Рассмотрим широкий класс законов фильтрации со степенной асимптотикой в области больших скоростей
Ф (до) ~ ФооШ* (до —у со), s > 0. (111.36)
Тогда при а/--*- оо уравнение (Ш.35) асимптотически переходит в
[s-W]' — 4~'n2ws-2P =0, (III.37)
Линейно независимые решения которого — степенные функции
Pi.2 = aA2, Г1. 2 = 2-1 [1 - s + Vsn2 + (1 - s)2]. <111.38)
Очевидно, показатели ru 2 вещественны и имеют различные знаки. Таким образом, одно из линейно независимых решений уравнения (II 1.37) можно выбрать убывающим на бесконечности, причем другое оказывается неограниченно возрастающим. Из сказанного легко заключить (и это можно доказать строго), что условием ограниченности на бесконечности выделяется единственное с точностью до множителя решение уравнения (III.35), которое при w-*-oо убывает как
Wr., г2 = 2—1 {< 1 — s) — [(1 — s)2 + sti2]1'2}. (111.39)
В частности, при линейном возрастании Ф(и>) в области больших скоростей s = 1, гч = — 1/2п, a Pn/2{w) убывает с ростом w как w~i/2n.
Таким образом, при w-+ со
Ф (w, 6) = g - + О (W). (II 1.40)
Тогда из (II 1.28) и (II 1.29) имеем
H = H(w) = ±[ -%-dw, х + iy = гё\ 2% J иг
* —г = -ф=±.. ,1,1.41,
Очевидно, формулы (111.40) и <111.41) описывают плоско-радиальное фильтрационное течение вблизи источника. Течение обладает осевой симметрией; распределения скоростей фильтрации и функции тока не зависят от вида закона фильтрации, линии тока — радиусы, исходящие из источника; скорость убывает обратно пропорционально расстоянию от источника, линии постоянного напора—концентрические окружности с центром в источнике.
Тем самым показано, что при любом законе фильтрации Ф(ш) и любой геометрии пласта течение в промежуточно-асимптотической области р<Сг<С/?, где р — радиус скважины; R — внешний масштаб пластовой системы (например, расстояние между скважинами или расстояние от скважины до границы пласта) — простейшее плоско-радиальное течение. Используя (111.41), легко находим формулу, связывающую расход фильтрационного потока с перепадом напора #i—Н2 между двумя концентрическими линиями постоянного напора:
«ч
= 5^7- (IH.42)
Ш,
.1-S
(II 1.44)
|
В частности, при фильтрации с предельным градиентом Ф (ш) — w + X и степенном законе фильтрации Ф (w) = W имеем, соответственно, |
|
|
|
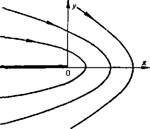
РИС. 23. Обтекаьие фильтрационным потоком непроницаемой полупрямой |
Если Г\ С Г2, последнюю формулу можно упростить, положив
S< 1.
2w,
2 / 1 — S
(III.45)
Таким образом, при подсчете дебита плоского фильтрационного потока со степенным законом фильтрации можно рассматривать задачи с контуром питания, унесенным в бесконечность при s>l или с нулевым радиусом источника (при s<l), что невозможно в случае линейного закона фильтрации и закона фильтрации с предельным градиентом.
Обратимся теперь к последующим членам разложения (III.34). Все они имеют однотипную структуру произведения
Pi (w) sin /9, (III.46)
Убывающего на бесконечности решения уравнения (III.35) и гармонической функции угла.
|
Я |
Естественно поставить вопрос о том, какому течению соответствует такое произведение. Поскольку sin /6 обращается в нуль при 6 = 0 и 6 = ц,'1 = 60, часть оси 0л; и прямой, составляющей с нею угол Є0, образуют единую линию тока. Поэтому можно ожидать, что решение (III.46) соответствует внешнему обтеканию клина с углом при вершине а0 — я — во. Такая интерпретация справедлива при I > 1. Более детальный анализ подтверждает это допущение. Вблизи вершины клина скорость фильтрации обращается в бесконечность (это обычный формальный результат, связанный с предположением о бесконечной кривизне линий тока вблизи вершины угла). В частности, при 1=1 получаем решение задачи об обтекании непроницаемой полупрямой, т. е. бесконечно тонкого клина (рис. 23). Соответствующее ему уравнение (III.35) принимает вид
-^Р = 0.
|
(III.47) |
W
Легко убедиться непосредственной проверкой, что решением этого уравнения, удовлетворяющим условию убывания на бесконечности, является выражение
Pt(w)= 1/Ф (w). (111.48)
Используя (III.28) и (III.29), найдем, что решение задачи об обтекании фильтрационным потоком непроницаемой полупрямой дается выражениями
Оо
Г—^________ !_ (e2ie —1)
J и2Ф (и) 2Фш ^ >
Решение (II 1.49) обладает рядом примечательных особенностей. Прежде всего заметим, что г — (х2 + У2)1/2 00 при w -> 0 и фиксированном 8, так что течением охвачена вся плоскость независимо от вида закона фильтрации.
В то же время при наличии предельного градиента давления Ф (0) = X > О при w -> 0 функция тока ф (w, 0) ограничена значением Q/X и, следовательно, расход фильтрационного потока конечен. Если же X = 0, то, так же, как и в соответствующей задаче линейной фильтрации, расход потока бесконечен. Другая интересная особенность найденного решения обнаруживается, если рассматривать плоскость хОу как вертикальную и вычислить изменение величины у вдоль линий тока ф = const. Согласно (III.29) и (II 1.49) имеем
Dy+s^dH = dy—$dH = 0,
Так что вдоль линий тока
У — (ф/<?)Я = const. (111.50)
Если взять ту линию тока, на которой if) = Q, то на ней будет постоянна величина Н — у. Заметим теперь, что если плоскость хОу — вертикальная с осью Оу, направленной вверх, то разность Н — у будет пропорциональна гидростатическому давлению. Следовательно, найденное решение отвечает течению в вертикальной плоскости, для которого на одной из линий тока давление остается постоянным. Тогда, рассматривая лишь верхнюю полуплоскость у> 0, можно взять эту линию тока за свободную поверхность и получить точное решение задачи безнапорной фильтрации при нелинейном законе сопротивления. Это решение, найденное Энгелун - дом, является обобщением классического решения Н. Е. Жуковского о безнапорном притоке к дренажной щели, расположенной на водоупоре.
|
X + iy = Q |
Рассмотрим асимптотику решений в области малых скоростей. Если в области фильтрации имеется точка (критическая точка) или застойная зона, в которой скорость фильтрации обращается в нуль, то эту критическую точку можно окружить замкнутой линией Гш, на которой модуль скорости фильтрации принимает постоянное значение (О и внутри которой нет других особых точек потока. Область £>« между линией Гт и критической точкой (застойной зоной) на плоскости годографа отображается в полосу
Дш : 0 < w < со, причем удобно считать ее бесконечной по в : — оо< < 0 < со, поскольку при каждом обходе вокруг критической точки угол 8 получает приращение 2тгN. Целое число N назовем кратностью критической точки (застойной зоны). На границе застойной зоны (в критической точке) функция тока принимает постоянное значение, которое можно принять за нуль. Таким образом, задача сводится к тому, чтобы в полосе Дш найти решение уравнения (111.30), обращающееся в нуль при w = 0, и периодическое по 0 с периодом 2kN. Это решение имеет вид
Ф (w, 6) = £ Pn/N (w) Га, Sin f+Bn cos ^ . n= і L
Здесь P7(w), обращающееся в нуль при w=0, —решение уравнения (111.35) с l = n/N-, Ап и Вп — постоянные.
Соответствующие формулы для напора и координат имеют вид
" = КЙЦ*. » Ж -«.»<■?] + »ns., (ш
П= 1
Dz = е" [—Ф-ЧН + iw-Щ).
Из выражений (III.52) следует, что вид прообраза линии w — 0, — оо < 0 < со на физической плоскости вполне определяется асимптотикой решений РТ (w) при w -> 0.
Действительно, на границе застойной зоны имеем
Dz = dx + idy = е« f = - е« Hm ( Щ rffl = = - e" S I - (SSL stag + 5„cos (111.53)
(III.51)
Л=І»,оГН dw )\ N " N,
Из анализа решений PT (w) несложно установить, что при l> 1 существует конечный предел
|
(II 1,54) |
|
ШФ' (w) dw |
Ф dPJ~(w)
Xi = Hm
Ш-►О
Для любого вида закона фильтрации. При этом xi= 0, если Ф (0) = 0 и xi ^ если Ф(0) = Х=£0, а если /< 1, конечный предел существует при фильтрации с предельным градиентом, для степенного же (или асимптотически степенного) закона фильтрации указанный предел равен бесконечности. Таким образом, можно сделать важный вывод о том, что в отсутствие предельного градиента давления в потоке могут существовать лишь изолированные критические точки, находящиеся в конечной части плоскости, если все %і=0{1 >1), или в бесконечно удаленной точке, если найдется такое п, для которого I =n/N= 1. Иными словами, топологическая структура фильтрационного потока при отсутствии предельного градиента остается такой же, как и при линейном законе фильтрации.
|
Ной области |
Если же имеет место фильтрация с предельным градиентом (Ф(0)=Х>0), то не существует изолированных критических точек потока; вместо них образуются области неподвижной жидкости (застойные зоны), остающиеся в конечной части плоскости или уходящие в бесконечность.
Особенно сложной оказывается структура потока при фильтрации с предельным градиентом в окрестности бесконечно удаленной точки. Если предельного градиента нет, то из требования ограниченности функции тока на бесконечности следует, что либо там расположена критическая точка, либо сток (источник) и линии тока стремятся к радиально расходящимся лучам (6=const).
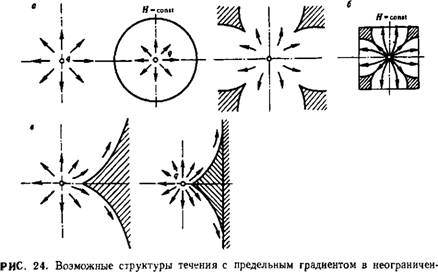
При фильтрации с предельным градиентом можно получить сколько угодно решений с ограниченной на бесконечности функцией тока; они отличаются расположением уходящих на бесконечность застойных зон. Такая неединственность решений задач фильтрации с предельным градиентом в неограниченных областях не указывает на их дефектность, а отражает специфическое свойство «дальнодействия»: если мы вносим в поток препятствие, а затем «уносим» его в бесконечность, то «память» об этом препятствии не исчезает полностью, как при линейной фильтрации, а остается в виде уходящей на бесконечность застойной зоны. Так, на рис. 24 показаны три различные структуры течения, создаваемого уединенным источником в бесконечной плоскости, получаемые предельным переходом из трех различных течений — осесим - метричного притока к центральной скважине в круговом пласте (а), притока к центральной скважине в пласте, имеющем в плане форму квадрата (б), а также притока к скважине вблизи непроницаемой прямолинейной границы (в). Предельный переход к
Течению в неограниченном пласте осуществляется увеличением линейного размера L до бесконечности.
Предельное равновесие. Особенность, принципиально отличающая фильтрацию с предельным градиентом, заключается в отсутствии движения жидкости при непостоянстве распределения давления по пласту, если только градиент давления не превосходит по модулю предельное значение G. В том случае, когда в каждой точке пласта |Vp| = G, распределение давления называется предельно равновесным. Слово «предельный» означает, что даже малое изменение давления может привести к началу движения. Если на некоторой линии (в пространственном случае — поверхности) С, ограничивающей область D, задано давление, то найти предельно равновесное распределение давления в D можно, решая уравнение
|Ap|=G, MЈD, (III.55)
При граничных условиях р = /(х, у, z), М ЈdD = С. Это уравнение имеет многочисленные аналоги в других областях физики. Например, уравнение эйконала в геометрической оптике, имеющее вид (III.55), если поверхности постоянного давления считать волновыми поверхностями. Нормали к этим поверхностям — линии направления градиента давления — оказываются при этом прямыми, а семейство поверхностей постоянного давления — семейством поверхностей, находящихся друг от друга на фиксированном расстоянии (эквидистантных).
|
ЛН/ld |
|
Q'lL |
|
0 |
Рассматриваемая задача в двумерном варианте имеет и другой весьма наглядный аналог. Если функция р (х, у) — решение этой задачи, то она в некотором масштабе описывает форму поверхности сыпучей среды («песка»), если на контуре С задана
толщина слоя песка. Нетрудно сообразить, что предельно равновесные распределения давления могут не удовлетворять принципу максимума, если не сделать оговорок (см. п. 1).
Пусть на плоскости заданы эксцентричные окружность радиуса R и расположенная внутри нее окружность радиуса р («контур питания» и «скважина»), на которых заданы давления Р{ и Р2 соответственно. Построим на каждой из ннх конические поверхности «воронкой» вверх и вниз с наклоном образующих G
Pt~ = Я, ±G[R2-(x2+y*)]U2,
РІ = Pi ± G [(* - 8)2 + y2- p2]1/2 (111.56)
И положим
P+ (*> у) = max (pf, pi),
P~(x, y) = min (pt, pi). (111.57)
Нетрудно понять, что функциям р+ и р- соответствуют два предельно равновесных решения задачи (III.55)—верхнее и нижнее.
Это показывает, что предельно равновесные состояния определены не единственным образом; существенно уметь находить именно те предельно равновесные или просто равновесные состояния, которые реально достижимы в ходе некоторого нестационарного процесса.
Приведем некоторые результаты расчета основных элементов течения при фильтрации с предельным градиентом.
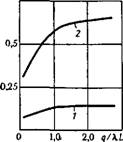
На рис. 25 показана зависимость относительной площади застойных зон, образующихся внутри кольцевой батареи п равно - дебитных скважин, от относительной интенсивности потока, а на рис. 26 — индикаторные кривые скважины в центре кругового контура питания радиуса R.
Во всех случаях расчеты проведены для относительного радиуса скважины р/R = Ю-3.
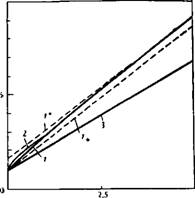
Влияние предельного градиента давления сказывается не только в образовании застойных зон, но и в общем усилении неравномерности потока, проявляющемся в концентрации основного потока внутри относительно узкой струи. Количественно эту особенность иллюстрирует рис. 27.
|
РИС. 27. Зависимость ширины трубки тока от интенсивности потока q/lL при фильтрации с предельным градиентом. Расход через квадратный элемент пятиточечной сетки в %: 1 — 20; 2 — 80 ДI/L
|
Основные проявления «псевдопластической» нелинейности типа фильтрации с предельным градиентом давления — увеличение перепадов давления и усиление присущей потоку неравномерности, вплоть до образования застойных зон. Эффекты эти становятся особенно значительными, когда мала интенсив
ность потока (q/lL< 1). Как показано ниже, эти основные закономерности сохраняются и для более сложных течений, в том числе и в задачах вытеснения нефти водой.
Задача 1. Используя соотношения (III.23) — (III.24), показать, что для обобщенной трубки тока любой формы перепад давления при фильтрации с предельным градиентом удовлетворяет неравенству
BpD + L^G = bpD + bpQ, (III.58)
Гд? Дод—перепад давления, рассчитанный при G — 0; L —минимальное расстояние между «входом» и «выходом» трубки тока; Др0 — пороговый перепад давления, при котором начинается движение.
Задача 2. Построить отображение на плоскость годографа скорости фильтрации элемента симметрии течения, создаваемого кольцевой батареей п равно - дебитных стоков интенсивности q и центрального источника интенсивности Q = nq. Как при такой геометрии течения будет располагаться застойная зона в случае фильтрации с предельным градиентом?
Задача 3. Показать, что для уравнения закона фильтрации вида
Ф (w) = (w2 + Х2)1/2 (III.59)
Функция ф может быть выражена через гармоническую вспомогательную
Функцию. (Этот результат впервые получен С. В. Панько.)
Задача 4. Показать, что при произвольном законе фильтрации уравнение (III.30) допускает частное решение вида
W
Ф (w, 0) = Pf и sin6, Р~ (w) = [Ф (ш)]-1 J оФ'(о) dv. (III.60)
О
Указать гидродинамический смысл полученного решения; проанализировать его структуру для степенного закона фильтрации и для фильтрации с предельным градиентом.
Зад а чл Показать, что при нелинейной безнапорной фильтрации образом свободной поверхности на плоскости годографа служит кривая [43]
—Ф(ш) + С sin 0 = 0, C=kpg/f>.. (111.61)
Задача 6. Используя формулу (II 1.42), получить связь между дебитом и перепадом давления для притока к скважине при двучленном законе фильтрации — см. формулу (1.13).