ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Процессы тепло — и массопереноса в пористой среде
Рассмотрим пористую среду, насыщенную однофазной жидкостью. Будем считать, что жидкость содержит растворенное вещество (примесь), массовую концентрацию которого мы обозначим через с. В то же время допустим что часть примеси а в расчете на
единицу объема среды может содержаться в скелете пористой среды. Поглощение скелетом примеси будем называть сорбцией; понимая под этим адсорбцию (физическую и химическую) примеси на поверхности скелета, растворение (абсорбцию) примеси в материале зерен скелета, а иногда даже механическое удержание примеси в сужениях поровых каналов (это существенно для полимерных растворов). Плотность раствора в соответствии с общими термодинамическими положениями определяется концентрацией, температурой и давлением:
Р = р(с, Т. р). (V. I)
Поэтому в единице объема пористой среды содержится примеси и растворителя, соответственно,
Mc + а, т(р—с). (V.2)
Фильтрационный поток со скоростью фильтрации w переносит как растворитель, так и примесь. Легко убедиться, что для смеси форма уравнения неразрывности остается неизменной. Чтобы составить баланс растворенного вещества, необходимо рассмотреть структуру потока примеси через границу выделенного объема. Этот поток состоит из нескольких различных по своей природе составляющих. Одна из них соответствует переносу растворенного вещества общим потоком, характеризуемому плотностью потока массы:
Q1 = cw. (V.3)
Этот поток существует даже при равномерном по объему пористой среды распределении примеси, если жидкость движется. Если примесь распределена неравномерно, то даже в отсутствие общего потока (w = 0) будет происходить перераспределение ее, обусловленное диффузией. Как известно, диффузия вызывается хаотическим движением на молекулярном уровне; чтобы подчеркнуть это, будем называть ее молекулярной диффузией. Согласно основному закону диффузии (закону Фика), для изотропной среды диффузионный поток пропорционален и противоположен по направлению градиенту концентрации:
QD = — Z)vc. (V.4)
В пористой среде примесь может, вообще говоря, диффундировать и в твердых зернах, и по поверхности контакта скелета с поровой жидкостью (поверхностная диффузия), так что закон Фика нуждается в уточнении. Эти эффекты несущественны для наших целей. Поэтому в дальнейшем используется выражение для диффузионного потока в форме (V.4) с коэффициентом диффузии D, постоянным и близким к коэффициенту молекулярной диффузии в жидкости.
Существенно, что в пористой среде при наличии фильтрации должен существовать, наряду с уже рассмотренными конвективным переносом и молекулярной диффузией, некоторый механизм переноса, обычно называемый дисперсией, обусловленный пространственными флуктуациями поля скоростей фильтрационного движения (т. е. отклонением локальных значений истинной скорости от среднего значения w) [12].
Для пояснения закономерностей этого механизма напомним, что коэффициент диффузии в газе равен по порядку величины произведению пульсации скорости (имеющей порядок скорости звука са—103 м/с) на длину свободного пробега (X—Ю-9—Ю-10 м), Dm — Сак - Подобно этому пространственные флуктуации поля фильтрационных скоростей вызывают как бы диффузионное перемешивание, называемое конвективной диффузиейкоэффициент диффузии для которого по порядку величины должен быть равен произведению флуктуации скорости (имеющей порядок скорости фильтрации w) на масштаб флуктуации /. Если этот масштаб считать равным внутреннему масштабу пористой среды d, то
D'~wd. (V.5)
При обычных скоростях фильтрации это произведение невелико (~10~10 м2/с) и поэтому имеет порядок коэффициента молекулярной диффузии для жидкостей. Однако те же соображения применимы к перемешиванию, обусловленному флуктуациями скорости любого масштаба вплоть до 1 —10 м. Вообще говоря, конвективная диффузия происходит тем быстрее, чем сильнее выражена неоднородность пласта и чем шире спектр размеров неодно - родностей. Это важное обстоятельство необходимо учитывать при всех оценках роли конвективной диффузии. В тех случаях, когда оценок недостаточно и нужны более точные количественные расчеты, приходится прибегать к экспериментальному определению коэффициентов конвективной диффузии.
Пространственные флуктуации поля скоростей приводят к дополнительной дисперсии не только в направлении движения, но и в поперечном направлении. Нет оснований ожидать, даже для изотропной среды, что «поперечная» дисперсия будет происходить с той же скоростью, что и «продольная». Поэтому необходимо вводить продольный и поперечный коэффициенты дисперсии
D и = /и w, D± = lLw. (V.6)
Из изложенного следует вывод, подтверждаемый более детальным анализом. Именно в реальных пористых пластах процесс дисперсии доминирующий. Для него справедлив закон Фика, однако этот процесс анизотропен, и коэффициент диффузии растет с ростом скорости; выражение для потока имеет вид
Q) = —D'ijdc/dxc. (V.7)
Тензор коэффициентов дисперсии (конвективной диффузии) Dij имеет в изотропной среде в качестве одного из главных направлений направление скорости фильтрации и в соответствующих главных осях принимает диагональный вид:
Dh = ltw, D22 = D33 = l±w, D'i2 = D'23 = D31 = 0. (V.8)
Коэффициенты /її и І!, имеющие размерность длины, определяются строением пористой среды и должны определяться для каждого объекта или класса объектов. Накопленный к настоящему времени материал, в основном, подтверждает приведенные соображения, хотя экспериментальная зависимость коэффициента конвективной диффузии от скорости ближе отвечает степенному закону
D'~w\ х=1,1 — 1,2. (V.9)
Можно убедиться, что степенной характер зависимости является следствием наличия у среды спектра масштабов неоднородности.
Запишем окончательно выражение для потока примеси:
Q = cw—Dvc; (V.10)
Qi = cwi — Dijdc/dXj; D„ = DM? Hj + D'ih (V. 11)
Тогда уравнение баланса примеси после обычных преобразований приводится к виду.
Д (тс + a)/di + div q = 0 (V. 12)
Или после подстановки выражения для q
(тс + a), t + V (wc) = v (DS7C). (V. 13)
Даже если поле скоростей w известно и известна зависимость тензора конвективной диффузии D от скорости, из уравнения (V.13) нельзя найти поле концентрации. Дело в том, что еще не задано распределение примеси между жидкой и твердой фазами. Наиболее общее допущение, которое будет использоваться, состоит в том, что скорость межфазного обмена примесью зависит от количества сорбированной примеси в единице среды а, концентрации примеси в растворе с и скорости фильтрации w:
A, t = 4 (с, a, w). (V.14)
Если сорбция обратима, то существует равновесное значение содержания сорбированной примеси:
А = а. (с, w), 9 (с, а (с, w), w) = 0. (V.15)
Если отклонение от равновесия невелико, то можно записать простейшее уравнение кинетики сорбции в виде
A t = —х-1 (а— а (с, а>)), т = — 1/<р. а (с, а, w) > 0. (V.16)
Этим уравнением и ограничимся, хотя в последующем может оказаться необходимым рассмотрение более сложных кинетических схем. Входящие в уравнение (V.16) функции а (с, w) считаются заданными. Определение их — экспериментальное, или из более детальной теории — особая задача, которая должна составить предмет специального рассмотрения.
В тех случаях, когда примесь может образовываться или уничтожаться, в правой части уравнений (V.13) и (V.14) должны быть дописаны члены, равные интенсивности генерации примеси, т. е. количеству примеси, образующемуся в единицу времени в единице объема пористой среды, соответственно, в жидкости и в материале скелета.
Путем аналогичных рассуждений можно записать уравнение баланса тепла для пористой среды. При этом, поскольку, как уже известно, время установления теплового равновесия между жидкостью и пористым скелетом мало, температуры их можно считать равными. При этом получим:
(СТ + m? i), , + v (рій) = V (XV Т) + Q. (V.17)
Здесь Т — абсолютная температура; i(p, Т) — удельная энтальпия жидкости; С — теплоемкость скелета в расчете на единицу объема среды. Тензор теплопроводности X учитывает и обычную (молекулярную) и конвективную теплопроводность, обусловленную, подобно конвективной диффузии, микронеоднородностью поля скоростей. Однако поскольку температуропроводность жидкости на несколько порядков выше коэффициента молекулярной диффузии, относительная роль конвективной теплопроводности обычно невелика, и ее можно не учитывать. В этом случае X превращается в обычный коэффициент теплопроводности насыщенной пористой среды.
Интенсивность тепловыделения Q учитывает тепловыделение за счет механической дисслпации, тепловой эффгкт химических реакций, тепловой эффгкт адсорбции и другие источники тепла. В задачах, рассматриваемых ниже, существенное тепловыделение происходит лишь при внутрипластовом горении; в прочих случаях им можно пренебречь.
Если не происходит фазовых переходов, то di — CpdT, где Ср— теплоемкость жидкости при постоянном давлении можно считать постоянной. Тогда, считая тепловыделение равным нулю, получим из (V.17) уравнение конвективной теплопроводности
D(mpCpT + CT)/dt + v (?СрТи) = v (XvT)- (V.18)
Используя уравнение неразрывности и считая X и С постоянными, преобразуем (V.18) к виду
Уравнение (V.19) с формальной точки зрения представляет собой упрощенный вариант уравнений переноса примеси (V.13) — (V.14) и потому может быть исследовано в рамках общей с ними теории. До тех пор, пока поле скоростей фильтрации считается известным, а тепловые и диффузионные процессы не связанными между собой, можно рассматривать гидродинамическую картину, массоперенос и теплоперенос последовательно и независимо друг от друга. Более того, ничего не изменится, если рассматривать произвольное число переносимых потоком примесей различной природы. Гораздо более сложная картина возникает, если существенно влияние примесей друг на друга и на гидродинамику. Рассмотрим пока основные особенности задачи о переносе фильтрационным потоком динамически нейтральной (т. е. не оказывающей обратного влияния на поток) примеси.
Будем считать, что заданы характерный линейный размер потока L и характерная скорость U. Тогда, вводя безразмерные координаты и время т,
Іi, = Xi/L, т = tU/L, (V.20)
Получим из (V.13) (V.14):
Д(тс + а) дс D д2с да L. .
—— + дТГ и^ = с' "У' Wi = UilU - (v-21 >
По сделанным оценкам при наличии макроскопического фильтрационного потока D — UI, так что D/UL — 1/L. Эта оценка показывает, что для переноса примеси в пористой среде число Шмидта (часто называемое также диффузионным числом Пекле PeD) Sh = = UL/D, характеризующее относительную роль конвекции и диффузии, имеет порядок отношения L/1 линейного размера потока к внутреннему масштабу пористой среды I и потому обычно много больше единицы.
Рассмотрим для уравнения (V.21) внешнее приближение, отвечающее по предыдущему (см. гл. IV) исследованию процесса в масштабах всего пласта, т. е. перейдем в системе (V.21) формально к пределу L оо. Тогда получим
{тс + a), t + wic. il = 0, ср (а, с, w) = 0, а = а (с, w). (V.22)
Соотношение (V.22) представляет собой уравнение переноса нейтральной примеси в крупномасштабном приближении. Физически оно соответствует пренебрежению диффузией и предположению о равновесном распределении примеси между твердой и жидкой фазами. Дифференциальные уравнения (V.22) легко интегрируются в общем виде для любого стационарного потока. Действительно, рассмотрим произвольную линию тока фильтрационного потока, определяемую параметрически условиями
Ds/dt = m~lw, dXi = m~lwit Xi{t0) = (V.23)
Здесь х°і — координаты жидкой частицы в момент t — to — характеризуют выбранную индивидуальную линию тока. Согласно уравнениям (V.22), скорость движения вдоль линии тока и можно считать известной функцией длины дуги S, и — u{s). Пусть в момент t = t° в точке М° {л:"} концентрация примеси равна с0. Рассмотрим точку М, движущуюся по линии тока Г°, проходящей через М° со скоростью
V(S)= u(s)[ffl + i,(l-'. (V .24)
При этом в точке М имеем:
Dc{M) _ де де _ де иі ("0 де____________ п
Dt ~ dt + '*ідхі~ dt +т + а<сдХі~
Таким образом, каждое значение концентрации примеси переносится по пласту вдоль линий тока со скоростью, равной скорости жидкой частицы и/т, умноженной на постоянный множитель (1 + - f - а с/т)-х, меньший единицы.
Весьма важно, что на перенос вдоль данной линии тока совершенно не влияет характер распределения примеси в поперечном направлении. Таким образом, в внешнем (крупномасштабном) приближении процесс переноса примеси описывается одномерным уравнением
^\тс+ о. (с, и (s))] + «| = 0. (V.25)
Как было упомянуто (см. § 2, гл. IV), общее решение этого уравнения имеет вид
S
T = t(c, s) = t0 + (l + A'(c)) J А = ± (V.26)
Это выражение определяет время прихода примеси заданной концентрации с в точку с координатой s вдоль линии тока. Ему можно дать иную, более ясную физическую интерпретацию. Рассмотрим узкую трубку тока, окружающую данную линию тока. Из условия неразрывности для ее нормального сечения ш (s) легко получим
О) (s) U (s) = СОоЫо = const.
Поэтому интеграл в (V.26) пропорционален объему 5 (s) трубки тока между сечениями, отвечающими значениям координаты so и s. Этот объем монотонно зависит от s, и его удобно использовать в качестве универсального параметра вдоль линии тока, так как уравнение переноса и его общее решение при этом принимают особо простой вид:
S(c) = So(c) + uo(*-*o)/m(l+4'(c)). (V.27)
Иными словами, в плоскости t, S каждое значение концентрации с переносится с постоянной скоростью, отношение которой к скорости потока Uo/m зависит только от с.
Дальнейшее исследование производится вполне аналогично анализу вытеснения в задаче Баклея — Леверетта. Начальными и граничными условиями определяется на плоскости t, S линия, вдоль которой заданы значения концентрации. Эти значения переносятся по проведенным через граничные точки прямолинейным характеристикам (V.27). Если характеристики не пересекаются между собой, то решение задачи оказывается (во всяком случае, при гладких начальных условиях) гладким. Если же характеристики пересек а - ются, то даже при гладком начальном распределении решение оказывается разрывным. Поскольку, как видно из (V.27), наклон характеристик в плоскости (/, S) пропорционален (1 + А, с)~1, характер решения вполне определяется начальными и краевыми условиями и видом изотермы сорбции а (с). Если начальное возмущение концентрации имеет вид «ступеньки»
С(s, 0) = Со, с (0, t) = с", (V.28)
То возникающая волна концентрации распространяется как ступенька с постоянной скоростью при
(с0 — Со) А" (с) < 0, се (Со, с°)
И в виде непрерывной вслны, если Еерно обратное неравенство. Если на отрезке (со, с ) знак кривизны кзотермы сорбции изменяется, то при помсщи соотнсшений (V.26) получаем комбинацию скачков и непрерывных волн.
При этом на скачках концентрации выполняется соотношение баланса примеси (см. гл. IV)
[с] + [Л] = У [с], [С] = С+—С - (V.29)
Результат исследования задачи о распространении по пласту заданного на входе (х = 0) начального скачка концентрации — условия (V.28) — удобно сформулировать в следующем виде.
Пусть Со < с0. Определим при Со < с < с0 функцию
А*(с)= min \а (с), А (с,) + а (с,) (с - d)l (V.30)
Которую назовем вогнутой оболочкой функции А (с). Если представить себе график А (с) вырезанным из жесткого материала шаблоном, то график Л„ (с) будет соответствовать форме нити, натянутой между точками с0, А (со); с0, А (с0) снизу на этот шаблон. Тогда устойчивое решение задачи о распространении скачка дается соотношением
S (с, 0 = uotjtn (1 + А[ (с)), (V.31)
Причем, как видно из (V.31), прямолинейным участкам Л# (с) отвечают скачки с (5, t), а вогнутым дугам — участки непрерывного изменения концентрации. Угловым точкам Л* (с) соответствуют участки постоянства с при изменении S. На рис. 57 показаны возможные типы решений, отвечающие различным формам изотермы сорбции а (с).
Аналогии между задачами переноса сорбирующейся примеси и задачами двухфазной фильтрации не ограничиваются описанием процесса в крупномасштабном приближении. В области скачков градиент концентрации и производная ее по времени, отвечающие крупномасштабному приближению, бесконечно велики, и, какими бы малыми не были диффузия и время релаксации, пренебрегать ими нельзя.
Будем действовать по аналогии с исследованием решения вблизи скачков насыщенности (см. гл. IV). Пусть £ — поверхность разрыва концентрации, отвечающая крупномасштабному приближению. Будем считать ее гладкой и введем в окрестности этой поверхности локальную подвижную систему координат Si, S2, їз. где S2 и — криволинейная ортогональная сетка координат на поверхности 2; Si — координата, направленная по нормали к ней.
Запишем уравнение линий тока фильтрационного течения:
R = R(M0, t), dR/dt = и (г).
Здесь М0 — положение отмеченной точки на поверхности разрыва при t = 0. Дальнейшее движение поверхности разрыва в силу соотношений на скачках описывается уравнением
Г = Rx (Mo, і), dRi/dt = и (r)jm [1 + A' (с (M0))] = V.
В локальной системе координат уравнения переноса примеси примут вид:
ДЛИЕ+^ - (KV0 (тс + а) + (»vE)с = V$ (DV «У
J-=(KVE)a = <?. (V .32)
В координатах S; переменные сна гладко изменяются по направлениям S2 и S3 и резко по направлению Si. Произведем растяжение переменных, положив
Tt = D-%, x = D-V. (V.33)
Упрощая полученные уравнения (опуская малые члены по аналогии с гл. IV), получим внутреннюю задачу:
|
D (тс + a) d2c. r - = С = Сь |
|
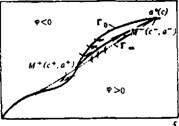
РИС. 58. К анализу уравнения (V.39)
|
= <P, c(+oo) = c±, a(+oo) = a±. (V.34)
Здесь un и Vn — нормальные к S компоненты скорости фильтрации и скорости скачка.
Краевые условия служат для согласования внутреннего решения с внешним. Интегрируя первое уравнение (V.34), получим с учетом условий на бесконечности
Ицс — Vn {тс + а) — VNdc/di = const = unc± — Vn (mc± + a±). (V.35)
Из второго уравнения (V.34) и условий на бесконечности получаем
A±=a(c±). (V.36)
Затем из (V.35) с учетом условий на бесконечности находим необходимое условие существования стационарного внутреннего решения, совпадающее с полученным раньше выражением для скорости скачка:
VN = uNlm (1 + [Л]/[с]); А = а/т. (V.37)
Это соотношение выведено в предположении, что искомое внутреннее решение существует. Чтобы доказать его существование, рассмотрим уравнение (V.35) совместно со вторым уравнением (V.34) и покажем, что они имеют решение с требуемой асимптотикой при +оо. Перепишем эту систему в виде dc
|
'di Un |
|
A — — r~ |
|
A — a~ + (c — c~) |
|
(1 + И1/[с]) m |
VNjr = Un (с - — с) + VN [т (с — с~) + а — а~] =
% = (V.38)
Система (V.38) не содержит явно независимой переменной С, и ее удобно представить на фазовой плоскости переменных а, с. Имеем
|
Vjtda D dt |
Изоклины нуля Г0: da/dc = 0 и бесконечности Г» da/dc = оо — уравнения (V.39) заданы, соответственно кривой а — а (с) и прямой а = а~ + (с — с-) Да/Ас. Эти изоклины обязательно пересекаются в точках (рис. 58) М - (с~, а~) и М+ (с+, а+) и разбивают представляющий физический интерес первый квадрант плоскости (с, а) на ряд областей, знаки производной da/dc в которых определяются следующим образом. При больших значениях а и малых с, очевидно, da/dc < 0; далее каждый переход через изоклину нуля или бесконечности приводит к смене знака. Поэтому для показанного на рис. 58 расположения изоклин точка М+ является седлом, точка М-—узлом, и имеется единственная интегральная кривая уравнения (V.39) —сепаратриса седла М+, соединяющая обе особые
Точки. Отвечающее ей решение обозначим через а0 (с). Если оно найдено, то из уравнения (V.38) имеем
Г (m + la)/[c])dc_______________________
J а0 (с) — а - + (с — с~) (а~ — а+)/(с+ — с~) "
При этом, как и должно было быть по условию задачи, интеграл расходится при c-vc±. Характер расходимости зависит от порядка касания линий Го и Г„ в соответствующих точках (см. гл. IV). Если эти линии пересекаются под конечным углом, то подынтегральное выражение в (V.40) имеет нуль первого порядка и С-------------------------------------
— In J с — с± |, так что
С~с± + С± ехр (-Т±С), 7+>0, т-<0. (V.41)
Если допустить, что линии Го и Г„ касаются друг друга, то подынтегральное выражение (V.40) имеет нуль более высокого порядка, и стремление концентрации к ее соответствующему предельному значению оказывается степенным:
С — с± = О (I С І—*), vі > 0. (V.42)
Заметим, что для возможности построения структуры скачка, т. е. внутреннего решений задачи, обладающего требуемыми асимптотиками, принципиальное значение имеет выполнение условий
А (с) >х (с-) + (Да/Д с) (с—с~), с+<с<с~,
А (с) < а (с~) + (Да/Дс) (с — с~), с+ > с > с~. (V.43)
Действительно, если это условие нарушается, не удается построить интегральную кривую, соединяющую точки М+ и М~, вдоль которой С изменилось бы монотонно. Таким образом, мы видим, что условия (V.43) необходимы и достаточны для существования внутреннего решения в виде равномерно движущейся волны концентрации. Поэтому, если ограничиться построением внешнего решения, из всевозможных вариантов разрывных решений, удовлетворяющих уравнениям баланса, нужно выбрать такие, для которых на каждом разрыве выполнены условия существования внутренней структуры (V.43). При этом получаем процедуру построения, описанную вышэ. Такие же соображения окажутся основными и в более сложных задачах, рассматриваемых в последующих параграфах.