ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ

Основные представления теории двухфазного течения в пористых средах

Распределение фаз в поровом пространстве. Капиллярное давление. Формирование залежей происхо­дит путем оттеснения из пластов-коллекторов первоначально на­ходившейся там воды. Поэтому вместе с нефтью и газом в коллек­торах всегда содержится некоторое количество (обычно 10—30 %, иногда до 70 % порового объема) так называемой погребенной воды. Кроме того, многие продуктивные пласты заполнены нефтью и газом лишь в верхней, купольной зоне, а нижележащие зоны заполнены краевой водой. Самые верхние части нефтяных зале­жей содержат газ, образующий так называемые газовые шапки. Таким образом, даже в ненарушенном состоянии в природных пластах может находиться несколько отдельных подвижных фаз. Двух - или трехфазное течение возникает практически во всех случаях разработки нефтяных месторождений, поскольку движу­щие нефть силы возникают вследствие упругости или гидравли­ческого напора газа или воды.

В данной книге рассматривается наиболее простое двухфазное течение, соответствующее вытеснению жидкости, первоначально заполнявшей поры, другой жидкостью, не смешивающейся с первой и образующей отдельную фазу. Говоря более конкретно, речь будет идти в основном о вытеснении нефти из пласта водой или газом.

Введем основные характеристики многофазного течения — на­сыщенность и скорость фильтрации. Доля объема пор в элемен­тарном макрообъеме, охватывающем данную произвольную точку, занятого 1-й фазой, называется насыщенностью порового пространства этой фазой в данной точке и обозначается s,. Оче­видно,

П

(IV. 1)

I=i

Где п — число отдельных фаз. Таким образом, в системе п фаз имеется п — 1 независимая насыщенность. В частности, при иссле­довании фильтрации двухфазной жидкости достаточно рассматри­вать лишь одну насыщенность.

Движение каждой из фаз можно охарактеризовать вектором скорости фильтрации данной фазы Ui. Аналогично скорости фильт­рации однофазной жидкости », определяется как вектор, проекция которого на некоторое направление равна объемному потоку і-й
фазы через единичную площадку, перпендикулярную к данному направлению. Следует помнить, что эта площадка пересекает как твердую фазу, так и другие подвижные фазы.

Граница двух фаз в пористой среде разбивается на множество искривленных участков, радиус кривизны которых сопоставим с размером пор. Как известно, на межфазной границе возникает капиллярный скачок давления, определяемый по формуле Лап­ласа

Ре=а(1/Я, + 1//?2), (IV.2)

Где а — межфазное натяжение; Ri и R2 — главные радиусы кри­визны поверхности раздела фаз в данной точке, близкие размерам пор.

Как отмечалось в § 2 гл. I, характерный размер поровых ка­налов имеет порядок V k/т, т. е. при обычной для песчаников про­ницаемости (10~13 м2) он составляет 5—10 мкм. Межфазное натя­жение на границе большинства углеводородных жидкостей и газов с водой находится в пределах 0,03—0,05 Н/м. Это означает, что капиллярное давление на границе углеводородов с водой состав­ляет —10 кПа.

Вследствие хаотической искривленности межфазной границы в порах при двухфазном течении возможно образование изолиро­ванных частиц каждой фазы. Представим себе изолированную кап­лю одной из фаз размером порядка характерного размера пор, окруженную другой фазой и твердым скелетом. При продвижении этой капли в порах радиус кривизны ее поверхности должен изме­няться от минимального до максимального радиуса пор, т. е. примерно на У k1m\. Тот же порядок будет иметь и разность радиусов кривизны переднего и заднего фронта капли при движе­нии. Это означает, что для проталкивания капли через пористую среду перепад давления на ней должен составлять величину, близ­кую к капиллярному давлению. Если и длина капли имеет порядок размера пор г, то для ее перемещения потребуется приложить градиент давления рс/г, т. е. порядка десятков и сотен МПа/м, что намного превышает существующие и возможные градиенты давления, возникающие в результате практически всех естествен­ных и искусственных процессов. Отсюда следует, что подвижна почти всегда только связная часть каждой из фаз, насыщающих поровое пространство.

Таким образом, капиллярные силы способны создать в порис­той среде градиенты давления, намного превышающие градиенты, создаваемые внешними воздействиями. Поэтому именно капил­лярные силы полностью определяют распределение фаз в порах. Капиллярное давление, согласно (IV.2) пропорциональное кри­визне межфазной границы, зависит от структуры порового про­странства и от преимущественной смачиваемости скелета пористой среды каждой из фаз.

Для каждой фазы, имеющей связную часть, можно ввести фазовое давление в точке рг, понимаемое как осредненное по элементарному макрообъему давление в связной части фазы. То, что в отдельных изолированных каплях давление может значительно отличаться от среднего, никак не будет сказываться на движении. Долю объема порового пространства в окрестности данной точ­ки, занятую связной частью фазы, в дальнейшем будем называть активной насыщенностью, долю несвязной части — пас­сивной насыщенностью.

На распределение фаз в порах, кроме поверхностного натяже­ния, значительное влияние оказывают преимущественная смачива­емость скелета породы одной из фаз и угол смачивания. Давление в менее смачивающей среду фазе будет выше на значение капил­лярного давления.

Капиллярное равновесие в пористой среде. Прежде чем перейти к выводу уравнений фильтрации двухфазной жидкости, рассмотрим условия равновесия двух несмешивающихся жидкостей разной плотности под действием гравитационных и ка­пиллярных сил. Гидростатическое равновесие двухфазной системы в образце пористой среды устанавливается в основном двумя пу­тями: во-первых, вследствие впитывания более смачивающей жид­кости (например, впитывание воды в сухой, т. е. насыщенный воз­духом, вертикально расположенный образец пористой среды) к, во-вторых, путем дренирования образца, когда менее смачиваю­щая фаза вытесняет более смачивающую. Последнее происходит, например, при вытеснении (оттеснении) воды газом сверху из пер­воначально водонасыщенного образца.

Рассмотрим элемент пористой среды, в котором две жидкос­ти находятся в состоянии равновесия под действием капиллярных сил и силы тяжести. В связной части каждой из фаз введем дав­ления pi и р2 (индекс 1 относится к более смачивающей фазе). Условия равновесия для элемента длиной dz имеют вид

Dpi/dz = pig; dp2/dz = p2g; d (p2 — p\)jdz = (pi — p2) g. (IV.3)

Разность давлений в фазах равна капиллярному давлению в дан­ном сечении. Поэтому из (IV.3) следует

DPc/dz = (Pl-P2)g. (IV. 4)

Изменение капиллярного давления с высотой происходит вслед­ствие уменьшения или увеличения насыщенности. Более смачива­ющая фаза имеет тенденцию преимущественно заполнять более мелкие поры, поэтому с ростом ее насыщенности радиус кривиз­ны границы раздела фаз должен увеличиваться. Предположим для определенности, что смачивающая фаза обладает большей плот­ностью, как это чаще всего бывает в условиях вытеснения нефти водой Тогда в состоянии гидростатического равновесия водона - сыщенность будет постепенно уменьшаться с высотой. В силу мик­ронеоднородности пористой среды вода при впитывании поднима-

1 Основным минералом большинства песчаных коллекторов нефти и газа является кварц, который лучше смачивается водой, чем нефтью или газом, т. е. гидрофилен. Гидрофильны чаще всего и карбонатные породы.

Ется выше, а при дренировании удерживается на более высоком уровне в системах поровых каналов малого диаметра по сравнению с кана­лами большего диаметра. Эта тенденция ослож­няется поперечными перетоками между канала­ми разного диаметра. В поперечном (горизон­тальном) направлении равновесное распределе­ние фаз по системам поровых каналов полностью определяется капиллярными силами.

Соотношение (IV.4) может интерпретиро­ваться как связь капиллярного давления с на­сыщенностью в дифференциальной форме. Из распределения насыщенности с высотой может быть получена зависимость капиллярного дав­ления от насыщенности

S = s(z), Pe(s) = (pi-p2)sz. (IV.5)

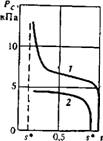
Кривые Pc(s), называемые кривыми капиллярного давления, представляют собой широко употребляемую интегральную характе­ристику структуры и микронеоднородности порового пространства. Вид связи Pc(s) зависит от направления изменения насыщенности, т. е. существует так называемый капиллярный гистерезис. Кривые Рс (s), соответствующие увеличению насыщенности более смачива­ющей фазой s, называются кривыми пропитки, а соответст­вующие уменьшению s — кривыми дренирования (рис. 36).

Кривые капиллярного давления, построенные по данным уста­новления гидростатического равновесия, на практике почти не ис­пользуют. Чаще всего их получают при медленном равновесном вытеснении более смачивающей фазы (воды или углеводородной жидкости) менее смачивающей (газом). Подробное описание ме­тодов получения кривых капиллярного давления можно найти в руководствах по физике нефтяного пласта.

Кривые капиллярного давления, отвечающие дренированию, ис­пользуются для оценки распределения насыщенности в так назы­ваемых переходных зонах на границе нефть — вода, газ — вода или газ — нефть в нефтяных и газовых месторождениях до нача­ла разработки. Это распределение непосредственно описывается формулой (IV.5).

Кривые капиллярного давления можно построить для различ­ных пар жидкостей и газов, отличающихся межфазным натяже­нием и краевыми углами смачивания на данной породе. Чтобы по­лучить функции насыщенности, характеризующие только структу­ру порового пространства, следует привести функцию капилляр­ного давления к безразмерному виду:

Рс = 2aVmJ(s, eyi 'k, (IV.6)

Где в — краевой угол смачивания. Формула (IV.6) получена по аналогии с выражением для капиллярного давления в одиночном цилиндрическом капилляре радиуса г: Рс = 2аcos9/г. В случае
пористой среды ввиду хаотического расположения стенок поровых каналов зависимость капиллярного давления от 0 не может быть выражена единой формулой. Тем не менее, по аналогии с круговым цилиндрическим капилляром Леверетт предложил записывать без­размерное выражение для капиллярного давления в виде

Pe = *VmcosQ0](s)lVk. (IV.7)

Выражение (IV.7) означает, что кривые капиллярного давле­ния считаются геометрически подобными при использовании раз­личных пар жидкостей в одной и той же пористой среде. Угол во в этом случае играет роль интегральной характеристики смачива­емости в системе пористая среда — жидкость. Функцию J(s) при­нято называть функцией Леверетта. Эти функции для разных типов пород-коллекторов нефти и газа систематизированы, напри­мер, в работах В. А. Иванова и др. [22].

Кривые капиллярного давления определены не для всех значе­ний s, поскольку при дренировании образца пористой среды вытес­нение более смачивающей фазы никогда не бывает полным. Оста­точная часть фазы находится в виде изолированных целиков в са­мых мелких порах или вблизи контактов между зернами. Неболь­шие изолированные целики, капли или пузырьки не могут быть вытеснены другой фазой при реально существующих градиентах давления. Поэтому в процессах как дренирования, так и пропитки существует некоторая насыщенность вытесняемой фазой (так называемая неснижаемая насыщенность), которая не уменьшается с ростом выталкивающего перепада давления. Если насыщенность меньше неснижаемой, капиллярное давление оказывается неопре­деленным, поскольку остаточная фаза состоит из отдельных не связанных между собой капель. Заметим также, что и при на­сыщенности больше неснижаемой часть вытесняемой фазы также находится в виде изолированных капель.

Когда насыщенность более смачивающей фазой приближается к неснижаемой, капиллярное давление быстро возрастает и на экспе­риментальных кривых капиллярного давления часто изображается неограниченный рост Рс при s^-s*. Физически более оправдано полагать, что при s -> s# капиллярное давление и функция Леве­ретта стремятся к конечным величинам, определяемым радиусом кривизны капель, составляющих пассивную насыщенность остаточ­ной смачивающей фазы.

Обобщенный закон Дарси для двухфазного течения. Теория фильтрации двухфазной жидкости во многом аналогична теории капиллярно-гравитационного равновесия. Как и в случае капиллярно-гравитационного равновесия, системы пор, занимаемые подвижной частью каждой фазы, следует представ­лять себе в виде каналов, протяженность которых в направлении движения намного больше, чем их размеры поперек потока.

Поэтому в первом приближении можно принять, что каждая подвижная фаза течет в занимаемом ею пространстве под дейст­вием «своего» давления, т. е. так, как если бы она была ограниче­на только твердыми стенками. Поскольку сопротивление движе­нию каждой фазы определяется только геометрией занимаемой ею части порового пространства, то закон фильтрации каждой из жидкостей двухфазной системы по Маскету и Леверетту можно записать в виде

В і = — (Mtlv-t) grad Pi, t=l,2, (IV.8)

Где fi — безразмерные величины, называемые относительными фазо­выми проницаемостями.

Пусть совместное течение двух фаз медленное, так что измене­ние насыщенности происходит квазиравновесным образом. Силы вязкого сопротивления можно рассматривать как распределенные массовые силы, пропорциональные скорости фильтрации. В одно­мерном случае из уравнений (IV.8) можно получить выражение, аналогичное по форме (IV.3):

Д (р2 — pi)/dx = Uі — U2\ Uі - y-iUi/kfi. (IV.9)

При выводе выражения (IV.4) неявно предполагалось, что PC(S)—характеристика, зависящая от структуры порового про­странства и поверхностных сил взаимодействия жидкостей меж­ду собой и с твердым скелетом, но не от гравитационных (массо­вых) сил. Это предположение подтверждается определениями кри­вых капиллярного давления с использованием различных жидкос­тей и путем центрифугирования [23]. Расуждая по аналогии, можно применить тот же вывод к распределению фаз в порах при медленной квазиравновесной совместной фильтрации, т. е. принять, что при данной насыщенности жидкости распределены так же, как и в условиях гидростатического равновесия. Это означает, во-пер­вых, что разность давлений в фазах р2—р\ может быть принята равной капиллярному давлению Pc(s) и зависящей только от насыщенности:

P2-pi = Pc(s) = <xVmJ(s)/Vk. (IV. 10)

Во-вторых, как уже отмечалось, капиллярные силы в поровых каналах существенно преобладают над внешним перепадом дав­ления и определяют распределение фаз в порах. Поэтому можно допустить, что каждая из фаз движется по «своей» системе поро­вых каналов, ограниченных твердым скелетом и другой фазой. Та­ким образом, при данной насыщенности гидравлические сопротив­ления, а следовательно, и проницаемость для каждой из фаз ока­зываются однозначно определенными.

Эксперименты показали [27, 48], что в широком диапазоне ус­ловий совместного течения и вытеснения двух фаз в пористых средах относительные проницаемости не зависят от скорости фильт­рации и отношения вязкостей движущихся фаз. Это можно объяс­нить тем, что поверхность соприкосновения (и сила взаимодейст­вия) каждой из фаз с твердым скелетом намного больше, чем с другой фазой. В некоторых исключительных случаях взаимодей­ствие подвижных фаз все же проявляется. Например, иногда
маловязкая вытесняемая фаза кратковременно образует для высо­ковязкой вытесняющей жидкости на поверхности скелета слой «смазки» и относительная проницаемость для вытесняющей фазы возрастает до значений, больших единицы. Но такой слой смаз­ки, по-видимому, неустойчив и существует недолго.

В дальнейшем изложении, если не оговорено противное, отно­сительные проницаемости и функция Леверетта считаются одно­значными функциями насыщенности, не зависящими от отноше­ния вязкостей.

Типичный вид функций относительной проницаемости для более смачивающей фазы fi(s), (s — ее насыщенность) и для менее смачи­вающей фазы /2 (s) показан на рис. 37. Эти кривые получены при стационарном совместном течении воды и нефти на малых образцах песчаника.

Характерная несимметричная форма кривых относительной про­ницаемости объясняется тем, что при одной и той же насыщенности более смачивающая фаза занимает преимущественно мелкие поры и относительная проницаемость для нее меньше. При малых насы - щенностях часть каждой из фаз находится в несвязном состоянии в виде изолированных мелких капель или целиков и не участвует в движении. Поэтому, начиная с некоторой насыщенности, каждая фаза полностью переходит в несвязное состояние и ее относитель­ная проницаемость становится равной нулю, т. е. fі (s) =s 0 при s < s#, /2 (s) = 0 при s > s* = 1 — a*.

Заметим, что хотя речь идет о совместной фильтрации двух не - смешивающихся жидкостей, приходится различать вытесняющую

И вытесняемую фазы, т. е. относи­тельные проницаемости, как и кри­вые капиллярного давления, раз­личны в зависимости от того, какая из фаз (более или менее смачива­ющая) первоначально заполняла пористую среду, т. е. существует гистерезис относительных проница­емостей, аналогичный гистерезису кривых капиллярного давления. «Неподвижные» насыщенности s„ и а» совпадают с «неснижаемыми» насыщенностями на кривых капил­лярного давления.

Итак, если распределение фаз в порах равновесно, для фильтра­ции двухфазной жидкости справед­ливы уравнения Маскета и Леве­ретта

Ui = — (kfi (s)/p.,) grad pt, i=l,2,

(IV. ll)

P2~P\=Pc(S). (IV. 12)

Чтобы получить замкнутую систему уравнений, необходимо за­писать уравнения сохранения массы для обеих фаз, которые вы­водятся совершенно аналогично тому, как уравнение неразрыв­ности для однофазного течения (1.16):

A(/np, s)-div (рія,) = 0, (IV. 13)

~ [mP2 (I —s)] — div (p2a2) = 0. (IV. 14)

Поскольку pi и P2 — функции давлений pi и p2, а изменение пористости в однородном пласте зависит только от изменения сред­него давления р = pis + р2 (1 — s), уравнения (IV. 11) — (IV. 14) обра­зуют замкнутую систему для pi и s.

Если вытесняемая и вытесняющая фазы — слабссжимаемые ка­пельные жидкости, влиянием сжимаемости на распределение насы­щенности часто можно пренебречь. Действительно, характерное время нестационарного перераспределения давления за счет сжи­маемости составляет ti — L2/*, где * — коэффициент пьезопровод - ности; L — характерный размер. Характерное время вытеснения t2 = L/u, где и — средняя скорость фильтрации. Обычно скорость фильтрации равна около Ю-3 см/с, L не более 104—105 см, а х ^ 104 см2/с. Поэтому ti/t2 = uL/% ^ Ю-2, откуда видно, что неста­ционарные процессы упругого перераспределения давления закан­чиваются в начале вытеснения.

Если жидкости и пористую среду можно считать несжимаемыми, вместо (IV. 13) и (IV. 14) получаем соотношения

Mds/dt — div «і = 0; mds/dt + div u2 = 0. (IV. 15)

Уравнения (IV. 15) замыкают систему уравнений фильтрации двухфазной несжимаемой жидкости (IV. 11) — (IV. 12).

Иногда неудобно использовать в уравнениях фильтрации рі и р2, так как давление в каждой из фаз не определено в тех областях, где соответствующая фаза неподвижна или отсутствует. Введение среднего давления в виде р = рis + Pi (1 — s) может быть удобно для учета сжимаемости скелета пористой среды, но приводит к до­вольно громоздким соотношениям при общей формулировке задач вытеснения. Для несжимаемых жидкостей оказывается удобным определить среднее давление по формуле

І

P = piF(s) + p2[l-F (s)] - J Pa (S) F' (s) ds, (IV. 16)

Где F (s) = /і (s)/[/i (s) + 1x0/2 (s)], [AO = (M/[»2.

Из (IV. 12) и (IV. 16) нетрудно получить 1

Pi = р + S Рс (S) F' (s) ds - Pc (s) [1 - F (s)],

S

1

P2=P+I Pc (S) F'(s) ds + Pc (s) F (s). (IV. 17)

S

Отсюда можно получить для суммарной скорости фильтрации обеих фаз и = и\ + и2 выражение

И = — (6<p(s)/iii)gradP, (IV. 18)

Де f (s) = /і (s) + P-0/2 (s).

Выражение (IV. 18) может рассматриваться как обобщение закона Дарси для суммарной скорости. Комбинируя соотношения (IV. 17) с уравнениями обобщенного закона Дарси и неразрывности, можно получить систему уравнений двухфазной фильтрации, содержащую только неизвестные Р и s:

Div [? (s) grad/3] = О, (IV. 19)

Ds/dt — div [(kfi (s)/mii|) grad P] — а2ДФ (s) = 0, (IV.20)

Где

S

Ф (S) = - W'(s) /2 (S) F (s) ds; a* = a j/^/ц, Vm 0

Д — оператор Лапласа.

Ограничения в применимости системы уравнений двухфазной фильтрации в форме (IV. 11), (IV. 12) и (IV. 15) связаны главным образом с действием трех факторов: неоднородности пористой среды, влияния гидродинамических сил на распределение фаз в порах и неравновесности.

Соотношение гидродинамических и капиллярных сил в порах может быть охарактеризовано безразмерным параметром [48]

Пс = Vkl I grad Р \/а Vm, (IV.21)

Где I — характерный размер порового канала, занятого одной фа­зой. Если в качестве I принять характерный размер пор yrk/m, то вместо Пс получим параметр

П* = &|gradP|/am. (IV.22)

Последний параметр часто записывается через скорость фильт­рации и = | (&/[i.) grad Р | и иногда называется капиллярным чис­лом Nc.

Nc = ujxi/a. (IV.23)

Экспериментальные исследования показывают, что параметр Nc при малых его значениях не влияет на вид кривых относительной проницаемости вплоть до некоторого критического значения N°. Со­гласно результатам Д. А. Эфроса [48], значение №с имеет порядок Ю-5, т. е. влияние гидродинамических сил сказывается на распре­делении фаз в порах, когда они на несколько порядков меньше капиллярных. Так как критическое значение Nc крайне мало, есть основания сомневаться в правильности выбора параметра Nc или ГС в виде (IV. 22) или (IV. 23). По всей вероятности, в опытах на довольно крупных образцах, проведенных Д. А. Эфросом и В. П. Оно­приенко, характерный размер (диаметр) каналов, занятых каждой фазой I, намного превосходил размер пор У к/т. В результате кри­тическое значение параметра Пс оказывается намного больше, чем критическое значение Пс или Nc. Характерный размер I определя­ется, по-видимому, неоднородностью пористой среды и тем больше, чем больше размер рассматриваемой области течения или образца породы («масштабный фактор»). Влияние неоднородности на рас­пределение фаз на макроуровне в связи с этим будет рассмотрено в § 5 данной главы.

В последнее время, в связи с широким применением поверх­ностно-активных веществ для повышения нефтеотдачи пластов рядом авторов проведены детальные исследования возможности уменьшения остаточной нефтенасыщенности при вытеснении путем снижения поверхностного натяжения на границе нефть — вода. С точки зрения теории двухфазного течения в пористой среде эти исследования сводятся к оценке влияния капиллярного числа Nc на «неподвижную» насыщенность. Эксперименты проводились на малых образцах с высокой степенью однородности и на модельных пористых средах или моделях элементарных пор. Эксперименты показали, что при Nc<0,05 остаточная насыщенность о* (ме­нее смачивающей фазы) не зависит от этого параметра, а при Nс>0,38 происходит полное вытеснение (о* = 0). При значениях скорости фильтрации, вязкости и межфазного натяжения, со­ответствующих условиям вытеснения нефти водой без примене­ния поверхностно-активных веществ, параметр Nc находится в пределах 10~6—Ю-4, т. е. влияние Nc на остаточную нефтенасы - щенность не должно наблюдаться. Заметим, что во всех экспери­ментах высокие значения Nc (до 0,1—1,0) достигались путем сни­жения межфазного натяжения до Ю-5—10~6 Н/м. Достигнуть вы­соких значений Nc путем увеличения скорости не удается вслед­ствие нарушения закона Дарси.

Рассмотренное влияние скорости на относительные проница­емости сказывается как в стационарных, так и в нестационарных условиях течения. В нестационарных процессах, кроме того, про­является влияние неравновесности распределения фаз (см. § 4 данной главы).

Трехфазная фильтрация. В предыдущем изложе­нии мы ограничились только случаем двухфазной фильтрации. В немногочисленных пока исследованиях трехфазной фильтрации закон фильтрации записывается в форме

И,- = — (kft(si, s2)/i»() gradph і = 1, 2, 3, (IV.24)

Pi — pj = PlJ (sb s2), і, /= 1, 2, 3. (IV.25)

Исследования относительных проницаемостей в системе трех фаз показали, в частности, что в системе нефть — газ — вода в гидрофильных средах относительная проницаемость для наиболее смачивающей фазы (воды) зависит только от водонасыщенности и не зависит от соотношения двух других фаз.

Уравнения неразрывности в трехфазной системе при условии несжимаемости фаз имеют вид, аналогичный (IV. 15):

Т (dsi/di) + div щ = 0. (IV.26)