ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ

Нестационарное движение однородных жидкостей. Нелинейные эффекты

Рассмотрим нестационарные изотермические движения газа в пористой среде и эквивалентные им безнапорные движения. При их исследовании выявляются нелинейные эффекты, характерные для многих задач подземной гидродинамики. На примере этих течений также хорошо иллюстрируются методы решения нели­нейных задач.

Основные уравнения фильтрации газа. При иссле­довании фильтрации газа основное значение имеет тот факт, что сжимаемость газа обычно на несколько порядков превышает сжи­маемость пористой среды. Поэтому можно пренебречь изменени­ем пористости т в уравнении неразрывности

(/лР)., + div Ри = 0, (11.141)

Которое приводится к виду

M^ + divp« = 0. (11.142)

Чтобы получить замкнутую систему уравнений, нужно исполь­зовать связь плотности газа с его давлением р и температурой Т р = р (р, Т), по этой причине в задаче появляется новая перемен­ная Т. Для замыкания системы уравнений необходимо добавить еще одно уравнение — уравнение энергии. Однако, если в среде отсутствуют источники выделения или поглощения энергии, то изменения температуры в процессе движения газа настолько ма­лы, что при расчете поля давления газа ими можно пренебречь. Это обстоятельство легко понять, если учесть, во-первых, медлен­ность фильтрационных движений и, во-вторых, наличие теплово­го балласта — скелета пористой среды, эффективно подавляющего изменения температуры. Будем считать, что

Р = р(р, Г0) = р(/>), (11.143)

Где То—постоянная температура.

Уравнения (11.142) и (11.143) и уравнение закона фильтрации

Я = — (k/p) grad р (11.144)

Образуют замкнутую систему. Исключая скорость фильтрации, имеем

<n% = k div^grad^. (11.145)

Ограничимся простейшим случаем, когда газ считается термо­динамически идеальным с вязкостью, не зависящей от давления.

Р = рро/ро; [J. = const. (11.146)

При этом уравнение (11.145) преобразуется к виду

Ґ = = (IM47)

Эти уравнения — уравнения изотермической фильтрации газа — были впервые получены JI. С. Лейбензоном [26]. Он же указал на их аналогию с уравнениями Буссинеска нестационарного по­логого безнапорного движения; эта аналогия позволяет рассмат­ривать исследование двух упомянутых классов движений как единую задачу. Независимо несколько позже аналогичное урав­нение было получено Маскетом.

Инвариантные задачи нестационарной фильт­рации. Нелинейность задач нестационарной фильтрации газа и безнапорной фильтрации не позволяет использовать разработан­ный аппарат линейных уравнений математической физики, для которых справедлив принцип суперпозиции решений. Поэтому в теории фильтрации (как и во многих других разделах физики вообще и механики сплошных сред, в частности) уже давно ис­пользуются своеобразные частные решения, которые выражают­ся через функции одной переменной. Вначале считалось, что их значение определяется тем, что они описываются обыкновенными дифференциальными уравнениями, решать которые проще, чем уравнения в частных производных. Для различных приближен­ных методов такие решения часто использовались как эталоны, позволяющие оценить точность метода.

Однако главная их ценность была осознана позднее. Оказа­лось, что таким путем асимптотически описываются фильтраци­онные течения для весьма широких классов задач, когда детали граничных и начальных услоьий перестают быть существенными. Именно эти области часто бывают наиболее интересными (например, спустя незначительное время после начала отбора из скважины, пока воронка депрессии не достигла области влияния соседней скважины и т. д.). Зная такие решения, фактически можно судить, по крайней мере, качественно, об очень широком классе фильтрационных движений (подробнее см. [4]).

Важным свойством рассматриваемых ниже решений является их инвариантность: для одних «автомодельных» — пространствен­ные распределения давлений, напоров, плотностей и т. п. оказы­
ваются во все моменты времени геоме­трически подобными, для других — кривые изменения этих параметров перемещаются, не меняя формы, с по­стоянной скоростью и т. д. Это свой­ство связано с особым характером за­дач, в которых после выполнения определенных преобразований зависи­мых и независимых переменных урав­нения, граничные и начальные условия задачи остаются неизмен­ными. Как говорят в математике, эти задачи инвариантны относи­тельно некоторой группы непрерывных преобразований. Такие задачи рассматриваются ниже.

Автомодельные пологие безнапорные движения при нулевом начальном уровне жидкости. Ниже рассмотрим точные решения некоторых нелинейных задач неста­ционарной фильтрации, характеризующихся нулевым начальным условием. Исследование этого класса движений представляет принципиальный интерес, поскольку в подобных задачах наиболее сильно проявляется существенно нелинейный характер рассмат­риваемой проблемы и обнаруживаются некоторые свойства нелинейных движений, резко отличающие их от соответст­вующих линейных задач и неизбежно утрачиваемые при линеаризации.

Для определенности при исследовании задач с нулевым на­чальным условием рассмотрим безнапорные пологие фильтраци­онные движения грунтовых вод в первоначально сухом грунте. Согласно обнаруженной Л. С. Лейбензоном аналогии, все полу­чаемые результаты можно непосредственно использовать для за­дач изотермической фильтрации газа. Излагаемые ниже решения были получены в работах [1, 2, 6].

Рассмотрим полубесконечный пласт, имеющий снизу плоскую горизонтальную непроницаемую границу—водоупор, а со сторо­ны канала — плоскую вертикальную границу (рис. 8), перпенди­кулярную к оси х и проходящую через точку х=0.

Пусть начальный напор жидкости в пласте равен нулю, а напор на вертикальной границе пласта изменяется по степенному закону, начиная с исходного момента t = t0:

H (х, t0) = 0, h (0, Q = a(/ —/о)', (11.148)

Где а > 0; a — некоторая константа, выбираемая в пределах —1/2< < a < 0. В частности, константа а может равняться нулю; в этом случае напор на границе мгновенно принимает некоторое значение а и остается постоянным. В случае фильтрации газа сформулиро­ванная задача соответствует его закачке при нулевом начальном давлении в однородный пласт постоянной мощности при изменении давления в начальном сечении пласта по степенному закону.

Линиями равных напоров будут линии х — const, параллельные границе пласта. Таким образом, напор h(x, t) — решение уравнения

Я-«5Г:<">49>

При условии (11.148).

Напор в некоторой точке пласта h зависит от координаты х, времени от начала процесса t—10, коэффициентов а и а и кон­станты а. Так как уравнение (11.149) однородно по времени, на­пор будет зависеть только от разности t—to, а не от значений f и /о в отдельности. Вводя для удобства независимую размер­ность напора (это возможно, так как для рассматриваемой за­дачи несущественно, что размерности длины и напора одинако­вы) получим размерности этих аргументов в следующем виде:

[а] = [ftj-W-[5], [t —10] = Т, [х] = L, [а] = [/і] Т-\ (II. 150)

Где [A], L и Т — соответственно размерности напора, длины и вре­мени; а — безразмерная константа. Из аргументов, от которых зависит напор жидкости, можно составить только две независимые безразмерные комбинации

АсТТ^тг;(11.151)

Используя анализ размерностей, выражение для напора можно представить в виде произведения комбинации определяющих па­раметров, имеющей размерность напора (в качестве нее можно взять a(t — toY), на безразмерную функцию от безразмерных ком­бинаций (11.151). Имеем, таким образом,

А = „(/ — /oYf(l, X); Х=а/(1 + а), (11.152)

Где / — безразмерная функция. Параметр X введен вместо парамет­ра а для удобства последующего изложения. Очевидно, что а лежит в интервале — 1 < X < 1. Имеем далее

Jt = ab(t — toY~lf (E, X) — о (f — toYx (a + 1) x

І Г " + ' ~ й ^ = °2 (t-tpfa{*+ L)

X 2 у m(t~t0)'+l Ж дх2 av(t-t0)« d.;2'

Подставляя эти соотношения в уравнение (11.149) и условия (11.148) и упрощая, получаем для функции f обыкновенное

Дифференциальное уравнение

^ + = 0 <ПЛ53>

С условиями f (0, л) = 1, /(оо, X) = 0. (11.154)

Напор и объемный поток (расход) грунтовых вод должны быть непрерывными функциями х и t. Используя закон Дарси, имеем для расхода, приходящегося на единицу ширины пласта, выражение

- ■< -- Т =- ^ С - vm f • ("■>»>

Таким образом, из требования непрерывности расхода следует непрерывность функции dfjdl.

При непрерывной f(l) и ЇФ0 требование непрерывности функ­ции df2/dX — 2fdf/dk совпадает с требованием непрерывности произ­водной /'(£). Однако при / = 0 из непрерывности df2jd% непрерыв­ность /' (?) не вытекает. Напротив, как будет видно далее, искомая функция /(?, X) имеет в точке, где / обращается в нуль, разрыв первой производной.

Второе условие (11.154) удобнее привести к другому виду. Ум­ножим обе части основного уравнения (11.149) на х и проинтегри­руем по х от нуля до бесконечности. В результате получим

Оо оо 2 2

$ * Idx=it Ixh =a I xd-^dx

^a(x~)x=o+a[h2(0, t)-h2(со, t)=ah2(0, t).

(Очевидно, что dh2/dx стремится к нулю при Х -У ОО быстрее, чем х-1, в противном случае f не стремилось бы к нулю при X - у оо).

Интегрируя в пределах or і = to до t при граничном условии (11.148), представив решение в форме (11.152), имеем

°° ПП2 if І \ 2 ct—1 ОО

I xh (X, t) dx = 'у--------- f е/ (5, /.) =

О 9

= flfA*(0, 0 dt = аа ---------------------

(напомним, что а считается удовлетворяющим неравенству —1/2 < < а < со), откуда получаем искомое условие в форме

ОО I » _ 1

J6/(5. (ІІЛ56)

В интересующей нас области и изменения а и Я, правая часть (11.156) конечна и положительна.

Итак, рассматриваемая задача свелась к отысканию решения обыкновенного дифференциального уравнения второго порядка (11.153) при условиях (11.154) и (11.156), непрерывного и име­ющего непрерывную производную от квадрата. Уравнение (11.153) инвариантно относительно группы преобразований

Ф (S, ц) = (11.157)

Т. е. если \) удовлетворяет уравнению (11.153), то и Ф(£, удовлетворяет этому уравнению при произвольном положительном

(і, что дает возможность понизить его порядок. Полагая по общему правилу

F(l, = X); ,*=lnS, )=d<r/d-q (П.158)

И принимая <р за независимую переменную, получим для функции ф уравнение первого порядка:

Dtycfy = — [6<р2 + 7?ф + ф2 + 2-[6] (1 — Х)<р + 4-'ф1/уф. (11.159)

Исследование этого уравнения показывает [1, 6], что его инте­гральные кривые разбиваются на I и II классы (рис. 9). Ни одна из таких интегральных кривых не пересекает ось ф в конечной точке. Кривые I класса вблизи начала координат стремятся к сов­падению с прямой линией ф = mot = —2? (a-f I)-1; на кривых II класса при у 0 ф -»- со. Лишь разделяющая эти два класса интегральная кривая сепаратриса пересекает ось ф в конечной точке. Соответственно этому интегральные кривые уравнения (11.153), удовлетворяющие условию f (0) = 1, располагаются, как покгзано на рис. 10. Кривые I класса при £ оо изменяются по згкону / = DЈ2X (D ф 0 — константа, различная для различных кривых), причем ни одна из них ни в одной точке не пересекает оси абс­цисс и, очевидно, не является искомой. Исключением является случай, когда а = 0 (рассматриваемый ниже), для которого все кривые I класса имеют горизонтальные асимптоты. На рис. 10 приведены зависимости / от ; при а > 0. Остальные интегральные кривые (кривые II класса) пересекают ось абсцисс в конечных точках, причем под прямым углом. Разделяющая эти два класса интегральная кривая приближается к оси абсцисс в точке £ = под острым углом v, 0 < v < тс/2.

Поскольку напор жидкости по физическим соображениям не может быть отрицательным 1, ясно, что искомая функция f (£, Я) должна каким-то образом комбинироваться из интегральных кри­вых уравнения (11.153) не принадлежащих к I классу, в той их части, где эти кривые располагаются над осью абсцисс, и из са­мой оси абсцисс. Однако, если составить функцию f (|, Я,) таким
образом, чтобы она представлялась отрезком некоторой кривой II класса вплоть до точки пересечения этой кривой с осью абсцисс и далее самой осью абсцисс, то полученная функция в точке £ = £с будет иметь разрыв производной от квадрата.

Разрыв производной на графике Р от \ соответствует наруше­нию непрерывности потока жидкости, что противоречит постановке задачи. Поэтому ни одна из функций /(S, X), составленной из ин­тегральной кривой II класса (при С ^ 0), продолжаемой на оси абсцисс, не может быть решением.

Искомым решением, непрерывным и обладающим непрерывной производной от квадрата, будет функция, представленная кривой, состоящей из отрезка интегральной кривой, разделяющей кривые I и II классов, вплоть до пересечения ее с осью абсцисс в неко­торой точке S = и совпадающей с осью абсцисс при S > So - Сама функция непрерывна по построению; проверим непрерыв­ность производной от квадрата в точке пересечения % = So (в ос­тальных точках эта непрерывность не вызывает сомнений, поскольку интегральная кривая состоит из двух участков гладких кривых). При подходе к точке £ — $о справа, где интегральная кривая сов­падает с осью абсцисс, предел (df2/dl)e=i0-fo равен нулю. При под­ходе к точке £ = So слева предел

(df2/d~)i=^ о = (2да;)-;=,о„0,

С учетом сказанного вышэ также равен нулю. Таким образом, для построенной функции производная df2/dЈ непрерывна.

Покажем теперь, что построенная функция удовлетворяет ус­ловию (11.156). Умножим обе части уравнения (11.153) на Е и про­интегрируем в пределах от S = 0 до % — со (или, что то же, до S = So, так как при S > So Х) = 0). Получим

Є. So £о 2 2

-xjs/(s, + +felLds = o. (Ц.160)

О о о *

Но вследствие непрерывности f и df2/d\ имеем

Dfdk = |'_2 /(S, X) d\ = — 2 J S/ (S, X)dS;

0 0 0 о

<2с2 .Г2 Ч jp2

-fK-л-тч-і.

0 0 0 откуда и из (11.160) получаем

So °°

X)dS = J 5/(Є, X)dS = (l +X)-1, (11.161)

О о

Что и требовалось доказать.

Таким образом, функция /(S, X) отличается от нуля лишь при 5 < а при S > So она тождественно равна нулю. Разумеется, величина So зависит от параметра X. В точке S = So функция /(S; X) имеет разрыв первой производной.

Из требования непрерывности функций f и df2/di и теоремы единственности решения дифференциального уравнения следует, что при составлении функции /(£, X) склеивание различных ин­тегральных кривых уравнения (11.153) можно производить только в точках, где f = О, откуда непосредственно вытекает единствен­ность построенной нами функции, т. е. единственность автомодель­ного решения.

Для эффективного вычисления функции /(£, X) удобно посту­пить следующим образом. Получим (например, численно) решение Ф (S, X) уравнения второго порядка (11.153), обращающееся при S = 1 в нуль и имеющее в этой точке конечную первую производную, т. е. соответствующее разделяющей интегральной кривой, прохо­дящей через точку S = 1. Можно показать, что эта производная равна — 1/4. Функция (S, X), равная Ф (S, X) при К1 и тожде­ственно равная нулю при S > 1, непрерывна и имеет непрерывную производную от квадрата, удовлетворяет уравнению (11.153) и условию при £ -> со, но условию при S = 0 не удовлетворяет.

Для получения искомого решения вспомним, что функция

/(S, Х) = |Х-2Ф(X) (11.162)

Также удовлетворяет уравнению (11.153) при произвольном (л. > О и обладает нужными свойствами непрерывности. Выберем теперь [а = [м таким образом, чтобы функция /(£, X) удовлетворяла также и условию f (О, X) = 1, тогда полученная функция /(£, X) будет удов­летворять всем условиям, налагаемым на искомое решение. Имеем

/(О, X) = 1 = !^2Ф(0, X) = откуда получаем

N=tf»/2(X). (11.163)

Значение So, начиная с которого /(S, X) == 0, очевидно, равно S0=^I = /V-'/2(X). (11.164)

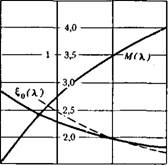
Результаты вычислений f (£, X) для ряда значений X приведены на рис. 11; на рис. 12 представлены функции Ео(Х) и М (X) — = —dp (0, X)/dS. Видим, что кривые /(£, X), соответствующие X > 1/2, обращены вогнутостью вверх; кривая, соответствующая X = 1/2, является ломаной, составленной из двух прямых; при Х< 1/2 кривые /(S, X) обращены вогнутостью вниз, причем вплоть до функции, соответствующей X = —1/2, производная /'(О, X) от­рицательна. Значению X = — 1/2 соответствует функция

/(S, - 1/2) = 1 - S2/8; 0<S<K8T/(S, - 1/2) = О, S > 1/8,

(11.165)

Имеющая f (0, — 1/2) = 0. При X < — значения /' (0, X) положи­тельны.

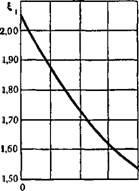
Функция £о(Х) монотонно возрастает с убыванием X, стремясь к бесконечности при X, стремящемся к —1 (решение, соответствую­щее X = —1, будет рассмотрено ниже).

Переходя от функции /(£, X) к напору жидкости h, получаем, что он отличается от нуля в каждый момент времени лишь в некоторой конечной части рассматриваемой области пористой среды, причем размер этой области со временем увеличивается. Конечность скорости распространения передней границы возму­щенной области характерна для рассматриваемого круга задач, отвечающих нулевому начальному условию; она существенно от­личает постановку задачи о пологих безнапорных движениях от задач, связанных с классическими линейными уравнениями пара­болического типа, для которых, как известно, бесконечна ско­рость распространения переднего фронта возмущенной области.

Эта особенность была впервые обнаружена в работах Я. Б. Зельдовича и А. С. Компанейца (1950) и Г. И. Баренблат - та (1952) путем исследования различных автомодельных реше­ний. Г. И. Баренблаттом и М. И. Вишиком (1956) было дано доказательство конечности скорости распространения передней границы возмущенной области для задач пологих безнапорных движений (а также широкого класса более общих задач), соот­ветствующих начальным распределениям напора жидкости, тож­дественно равным нулю вне некоторой конечной области.

Координата движущегося переднего фронта жидкости для рассматриваемых автомодельных движений выражается форму­лой

Хо (/) = So [ао (t — /0)*+7(а + 1)]1/2 (II. 166)

(поскольку передний фронт соответствует £ = £о); напомним, что параметры а и X связаны между собой соотношением X = а/(а - f 1). Скорость распространения переднего фронта vв представляется со­отношением

Vo = 2-Чв [ао (* — to)'-1 (а + I)]1/2.

В частности, когда напор на границе пласта постоянен, т. е. а = 0, то

Лго(*) = 2,286 Vao(t —10); v0 = 1,143yao/(t — t0). (11.167)

Далее, для суммарного объемного количества жидкости в пласте М получается следующее выражение:

За+1

M=$mh(x, t)dx = --^-^=J^------------------------ X)dS, (11.168)

О V « + 1 0

А для потока жидкости при *=0, т. е. для скорости притока жид­кости в пласт, в силу (II. 155) —выражение

-тс (£')„г -- (IL - (,U69)

Интегрируя обе части уравнения (11.153) по 5 от £ = 0 до S = оо или, что все равно, до S = So, поскольку /(S, X) = 0 при S > So, получаем

= (П.170)

В результате формула (11.168) приводится к виду:

О '+За

М = — - r^2rma1/V/2(l + а)'/2(/_/0) 2 _ (П.171)

Таким образом, предыдущие соотношения показывают, что реше­ния, соответствующие 0 < a < со, т. е. 0<Х<1, отвечают воз­растанию напора жидкости на границе и общего количества жид­кости в пласте; для решения, соответствующего a = X = 0, напор жидкости на границе постоянен в ходе всего процесса, количество ее в пласте возрастает. При —1/3<а<0, т. е. —1/2<Х<0, напор на границе в начальный момент бесконечен и убывает с течением времени до нуля; количество жидкости, первоначально равное, как и во всех предыдущих случаях, нулю, со временем увеличивается. При а = — 1/3, т. е. Х = — 1/2, напор на границе в начальный момент бесконечен и с течением времени убывает до нуля; общее количество жидкости в пласте постоянно в течение всего процесса — жидкость через границу і=0 в пласт не посту­пает. Во всех указанных случаях на границе пласта х = 0 во всякий момент времени достигается максимальное для этого мо­мента значение напора. При — 1/2 < a < — 1/3, т. е. — 1 < X < < —-1/2, напор жидкости на границе в начальный момент беско­нечен и с течением времени убывает до нуля. Общее количество жидкости в начальный момент бесконечно велико и с течением времени убывает, стремясь к нулю, так что на границе пласта жидкость уже не втекает в него, как в предыдущем случае, а вытекает. Тогда на границе пласта напор жидкости уже не будет максимальным; максимальное его значение достигается в некоторой внутренней точке пласта, различной для разных моментов времени.

Рассмотрим частный случай, соответствующий линейному воз­растанию напора жидкости на границе пласта, т. е. когда а=1. При этом

/1(0, t)=a(t—t0), i = xV2/aa(t — t0)-\ (11.172) а уравнение (11.153) принимает вид:

= <«■"»>

Как нетрудно проверить, функция

/($, 1) = 1-Е/2, 0 < S < Ео = 2, /(£, 1) = 0, £0<Е (II.174)

Удовлетворяет уравнению (11.173) и всем условиям задачи, откуда получается

H (х, t) = a(t — t0) — x (2а/о)-1/»,

0<л:< (2аа)'/2(/ —/0); (11.175)

H (х, /) = 0, (2ао)1^ (t ~ to) < х < со.

Координата переднего фронта жидкости (0 и постоянная скорость распространения переднего фронта выражаются следую­щим образом:

Х0(0 = (2aoy"(t — fo), vo = (2аа)'/2. (11.176)

Таким образом, график распределения напора жидкости а пласте представляется отсекаемым осями координат отрезком прямой линии, перемещающейся параллельно самой себе с посто­янной скоростью.

Предельные автомодельные движения. Рассмот­рим для того же полубесконечного пласта несколько иную зада­чу. Будем исследовать движение на полубесконечном интервале времени (—оо, t), поэтому начальное распределение напора по пласту несущественно.

Предположим, что на больших расстояниях от границы пласта, т. е. при л;->со, напор жидкости равен нулю, следовательно:

Й(со,/) = 0. (11.177)

Пусть, далее, напор жидкости на границе пласта возрастает со временем по экспоненциальному закону

/г(0, t) = h0e(11.178) а внутри пласта h (х, t) по-прежнему удовлетворяет уравнению

Д1г д2/12 С, ТТ

Ш = = (пл79)

Составим полный список аргументов, от которых зависит эта решение. Помимо координаты л: и времени t, в список войдут также величины А0, х и а. Тогда размерности всех определяющих параметров решения представляются в виде:

[x] = L, [t] = T, [a\ = [h]-'L2r-', [A0] = [A], [*] = T~l, (11.180)

Где по-прежнему символы L, T и [h] означают, соответственно, размерности длины, времени и напора. Из пяти аргументов (11.180) с тремя независимыми размерностями можно составить две неза­висимые безразмерные комбинации, которые удобно взять в виде х(х/аА0)1/2, х?. Отсюда и из анализа размерностей получается, что решение рассматриваемой задачи представляется в виде

Л = A0'f [х (аАо/х)—1/2, xt\, (11.181)

Где ср— безразмерная функция.

Положим t = + х, где х — произвольная константа. При этом условие (11.177) и уравнение (11.179), как нетрудно проверить, записываются через новую переменную Ґ, так же, как и через прежнюю переменную, а условие (11.178) принимает вид:

А (0, Ґ) = ho е *<; Ао = А0 е". (II. 182)

Таким образом, сдвиг во времени влияет лишь на некоторое преобразование величины А0, и постановка задачи оказывается ин­вариантной по отношению к группе преобразований переноса по времени; для определения А в переменных х, t, а, х, h'0 получа­ется та же задача, что и для определения А в переменных (11.180). Стало быть, на основе соотношений (11.181) и (11.182) имеем

H = Л0ср (xv, xt) = АрСр (xv, хґ) = = е"Ао<р (xv, х/ — хх); v = (x! ah0y2.

Отсюда следует, что при любом х справедливо тождество cp(Xv, xt) = е" ср (xv е-1/2*т, х/ — хх).

Положим X = t и получим

Cp(xv, xt) = е*'ср (xv е — 1/2х< , 0) = e^xve-1/2"'). (П.183)

Итак, функция А, зависящая от пяти аргументов (11.180), пред­ставляется через функцию одного аргумента:

А = А0е"'/(ї); 5 = xv ехр (—1/2*0- (11.184)

Подставляя (11.184) в основное уравнение (11.179), получаем для функции f(Ј) обыкновенное дифференциальное уравнение

Подставляя затем выражение (11.184) в (11.177) и (11.178), имеем граничные условия для функции /(?):

/(0)= 1, /(оо) =0. (11.186)

Вследствие непрерывности напора и потока жидкости функция /(;) по-прежнему должна быть непрерывной и иметь непрерывную производную от квадрата d\2jdl. Таким образом, для определения функции /(S) получили граничную задачу того же типа, что и граничные задачи для автомодельных решений, рассмотренных в предыдущем пункте, и соответствующую значению параметра а, равному бесконечности, т. е. Х= 1. Эффективное вычисление функ­ции f(l) выполняется способом, указанным выше, результаты вы­числений были приведены на рис. 11. Функция /(£) = /(£, 1) тож­дественно равна нулю при Е > So = 1,810; координата и скорость перемещения переднего фронта составят

Хо (0 = 1,810v е*'/2, do (t) = 0,905*v ext/2;

V = (аЛ0/*)1/2. (11.187)

Полученное решение в некотором смысле предельное для авто­модельных решений, рассмотренных в предыдущем пункте. В самом деле, положим в формуле (11.152) а = h0 (ат)-", где h0 — некоторая константа, имеющая размерность напора; т — константа, имеющая размерность времени. При этом, очевидно, эти константы выби­раются с точностью до некоторого постоянного множителя. Реше­ние (11.152) принимает вид

Будем неограниченно увеличивать а при стремлении начального момента io к минус бесконечности по закону

/о = — ах. (11.189)

Раскрывая неопределенность, получаем, что при а ^ оо

It — taY t а-1 /t — tn\a+l t

Уравнение (11.153) в пределе при он - со переходит в (11.185), а условия (11.154) совпадают с (11.186); /(S, X)-*/(?, 1) = /(Е).

Обозначая т через 1/х, получаем, что при а->-оо выражение (II. 188) стремится к (II. 184). Поэтому решение (II. 184) было названо предельным автомодельным решением [2]. Предельные автомодельные решения представляют и принципи­альный интерес в том отношении, что для доказательства их ав - томодельности уже недостаточно соображений анализа размер­ности, т. е. недостаточно инвариантности постановки задачи отно­сительно группы преобразования подобия величин с независимы­ми размерностями, как это было в ранее рассмотренных авто­модельных задачах, а требуется дополнительно воспользоваться инвариантностью постановки задачи относительно еще одной группы — группы преобразований переноса по времени.

Приведенные при рассмотрении предельной автомодельной за­дачи рассуждения носят общий характер и могут применяться во многих других задачах. Предельные автомодельные движения су­ществуют всегда, если система основных уравнений рассматривае­
мой задачи имеет автомодельные решения обычного степенного типа с произвольным показателем степени, который может принимать сколь угодно большие значения, и инвариантна отно­сительно преобразования переноса соответствующей координаты [4, 38].

Задача. На границе х = 0 полубесконечного пласта с непроницаемым горизонтальным водоупором задается поток (расход) жидкости как степенная функция времени

— о"С (дкг! дх)х=й = X (/ — t0f. Р > — 1, X > 0.

Начальный напор во всем пласте равен нулю. Решение задачи представляется в виде:

С2М2 (X) (р + 2)

Где М (к) = — df2 (0, X)/d; (см. рис. 13); координата переднего фронта жидкости л„(0 имеет вид:

9а2т (t ■

«о (0 = 60W

2CM (X) (р + 2)2

Осесимметричные автомодельные движения. При осесимметричных пологих безнапорных движениях напор жидко­сти удовлетворяет уравнению

Dh

Dt ~аТ'д?[Г дг

Где г — расстояние рассматриваемой точки пласта от оси сим­метрии.

Пусть в бесконечный пласт, ограниченный снизу горизонталь­ным водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим что начальный ее напор в плагте равен нулю, так что начальное условие имеет вид:

H (г, to) = 0. (11.195)

Предположим далее, что расход закачиваемой жидкости изме­няется со временем по степенному закону. Выражение для пол­ного расхода жидкости, закачиваемой через скважину радиусом Я, имеет вид:

Chf J =-*c(rf,

Drjr=R \ dr Jr=R

По предположению, радиус скважины пренебрежимо мал (ни­же остановимся на причинах, по которым это допущение можно делать для большинства реальных движений), поэтому можно принять Я = 0. Так как расход жидкости, закачиваемой в сква­жину, меняется по степенному закону, граничное условие на сква­жине принимает вид:

— я С (rdh2/dr)r=о = х (t — t0y, (II. 197)

Где х>0 и |3> — 1. В частности, случай |3 = 0 соответствует за­качке жидкости в пласт с постоянным расходом. Таким образом,

Q (t) = 2
решение задачи удовлетворяет уравнению (11.194) и условиям (11.195) и (11.197). По-прежнему, используя анализ размерности, можно показать, что это решение автомодельное и представляется в виде:

'х и TvVf (і X) ' х_ Р —с (г — W Л і (Є. X), Е-г^ теС(р+2)2 ) , Х -

Р +2" (11.198)

Как и прежде, искомая функция должна быть непрерывной и иметь непрерывную производную от квадрата. Подставляя выра­жение (11.198) в уравнение (11.194) и условия (11.195) и (11.197), находим, что функция /і (S, X) — решение граничной задачи

D L d? A, 1. dh w _ л e <

= — 1, /(оо, Х) = 0. (11.199)

5=0

Исследование этой граничной задачи проводится айалогично предыдущему, также единственным образом строится функция /і (£, X), отличающаяся от нуля лишь при 0 < S < Si (X), где Si (X)— некоторая функция X, а при S > Si (X) тождественно равная нулю. Функция /і (S, X), как нетрудно видеть из первого условия (11.199), при S -> 0 имеет особенность вида

/,(Е, X)^K-lnS, S^O. (11.200)

Второе условие (11.199) может быть приведено к другой форме: умножая уравнение (11.199) на S и интегрируя от S = 0 до S = со, а также используя дополнительно легко устанавливаемые из (11.199) условия (Sd/i/dS);=0o = 0, [S/i (S, Х)];=0 = 0, получаем следующее ин­тегральное соотношение:

» Еі(М 1

ЈS/,(S, X)dS = f S/i (S, X)dS = m. (П.201)

Oo

Эффективное вычисление функции /і (S, X) удобно проводить следующим образом. Строится решение задачи Коши Фі (S, X) для уравнения (11.199) обращающееся в нуль при S = 1 и имеющее в этой точке конечную первую производную. (Исследование показывает, что эта производная равна —1/4.)

Далее численно определяется величина

Lim (SdO?/dS) = — N(X).

Є-о

Величина N (X) оказывается не равной единице, поэтому функ­ция, равная Фі (S, X) при S< 1 и тождественно равная нулю при S > 1, удовлетворяет всем условиям граничной задачи (11.199), кроме условия в нуле. Воспользуемся теперь тем, что, как нетрудно показать, уравнение (11.199) и второе граничное условие инвари­антны относительно группы преобразований

Ф2(Е, X) = (S[*, X), (11.202)

Поэтому при произвольном положительном ]j. функция Фг(Е, X)

0,25 0,50 0,75 У. РИС. 14. Функции ^ (X)

Удовлетворяет уравнению (11.199) и второму граничному условию (11.199). Но

(MOl/dOs-o = (S, X)/dO?=о = — і*-W (X).

Выбрав (X = [х, = [N (X)]1/4, получим, что функция

/, (S, X) = [N (Х)]-1/2Фі (S[N (X)]'/4; X) (0 < 6 < Si (X)),

H (S, X) = 0, Si (X) = [N (X)]-'/4 < S < оо (11.203)

Удовлетворяет всем условиям граничной задачи (11.199).

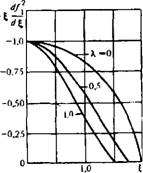
На рис. 13 и 14 показаны графики f\(S, X) при X = 0, 0,5; 1,0, а также график функции Si (X), через которую координата п среднего фронта выражается по формуле

Р+2

Сх (t — <„)' ит2 (р + 2fN (X)

В приложениях особо выделяются движения с постоянным рас­ходом закачки |3 = 0. При этом получается

(11.205)

R0(t)= 1,537 (а2х/С)Ч* Vt — ^o = 1,087(Ст/т9)Vt — tQ.

Задача о закачке или отборе газа через сква­жину. Рассмотрим горизонтальный пласт мощности Н, вскры­тый совершенной скважиной и содержащий в начальный момент газ под давлением P=const. Допустим, что через скважину, ради­ус которой г0, начинается закачка или отбор газа с постоянным массовым дебитом q, причем ^>0 отвечает закачке, a q<0 — от­бору газа. Тогда имеем

Dp2 kp і д ( др2\ , _ nktlfo і др2\ ...

Будем считать радиус скважины пренебрежимо малым (ниже приведем оценки, оправдывающие это допущение). Тогда условие (11.206) перепишется в виде:

<»■»">

Итак, искомое распределение давления в пласте, удовлетворяю­щее уравнению (11.147) и условиям (11.206), зависит от определяю­щих параметров г, t, a2, q*, Р.

Можно убедиться в автомодельности рассматриваемого движе­ния, так что распределение давления представляется в виде:

Р = m (Е, X), £ = г (a2Pt)-'/?, X = q'/P2, (11.208)

Где функция Fi (£, X) — решение граничной задачи d2F2 , dF2 g dFl / dF2\

JJ + Ы + = (IL209)

Качественная картина расположения интегральных кривых уравнения (II. 209) исследуется аналогично тому, как описано в п. 3.

Исследование показывает, что интегральные кривые, удовлет­воряющие второму условию (11.209), распадаются на два класса, разделенные между собой интегральной кривой Fi(ЈiX) = l, соот­ветствующей, как легко видеть, X = 0 (рис. 15). Кривые пер­вого класса, располагающиеся над кривой Fi (Е, 0) = 1, с умень­шением £ до нуля подходят к оси ординат, асимптотически уходя в бесконечность, так что при Е->-0 функция Fі (Е, X) медленно воз­растает по закону

Fi (Є, X) = (— X In Е)1/2 - f О (1). (11.210)

Каждой из интегральных кривых первого класса соответствует свое значение параметра X, монотонно возрастающее от нуля до бесконечности по мере удаления от кривой F\ (Е, 0) = 1.

При £ ->■ оо ординаты кривых обоих классов быстро стремятся к единице по закону

Л(«, Х)= 1+0[£-'ехр(-8-1£2)]. (11.211)

Кривые второго класса, располагающиеся под интегральной кривой F\ (;, 0)= 1, не доходят до оси ординат, а заканчиваются, подходя под прямым углом к оси абсцисс — особой линии урав­нения (11.209), поскольку на ней обращается в нуль коэффициент при старшей производной в этом уравнении. В таком случае вмес­то первого условия, которому удовлетворяют все интегральные кривые первого класса, соответствующие ^,>0, эти кривые удов­летворяют условию

(EdFi/dOe=T(X) = - X, (II.212)

Где Ё(Х)— координата точки пересечения рассматриваемой кривой с осью абсцисс. Каждой кривой соответствует определенное зна­чение X, монотонно убывающее от нуля до — оо по мере удаления кривых от интегральной кривой Fі (£, 0) = 1.

Интегральные кривые второго класса описывают автомодель­ные движения, в процессе которых происходит не нагнетание га­за в пласт, как в случае движений, отвечающих интегральным кривым первого класса (^>0), а отбор газа из пласта с расхо­дом, определяемым соответствующей этой кривой величиной

Q = \ъ/гНроР2/\>-ро (11.213)

(в этой формуле масссовый расход q считается отрицательным).

Следует отметить, что, создавая достаточный перепад давле­ния, можно, в принципе, закачивать газ в пласт с любым боль­шим расходом через скважину сколь угодно малого радиуса. Од­нако отбирать его из пласта можно лишь при расходах, не пре­вышающих того расхода, который соответствует установлению у стенки скважины нулевого давле­ния. Дальнейшее увеличение расхода отбираемого газа возможно только при условии расширения скважины. Таким образом, в от­личие от случая закачки газа нельзя ставить задачу об отборе его через скважину пренебрежимо малого радиуса. Кривые А,) при Х<0 (кривые второго класса) соответствуют авто­модельным движениям, когда отбор газа с постоянным расходом, определяемым формулой (II. 213), происходит через расширяю­щуюся скважину с радиусом, увеличивающимся по закону

R = £(к) (fl2Ptyi2 (11.214)

(причем на стенке этой расширяющейся скважины давление по­стоянно и равно нулю). Заметим, что расширение отбирающей скважины ни в коей мере не препятствует применению рассмат­риваемых решений к практическим задачам, поскольку для зна­чений параметра К, представляющих практический интерес, эта фиктивная скважина, как показывают проведенные расчеты (см. ниже), всегда будет находиться внутри настоящей скважины.

Для дальнейшего изложения полезно выяснить, какой порядок величины X встречается в практических задачах. Возьмем в ка­честве примера случай, для которого величина X будет весьма

РИС. 15. Интеграль­ные кривые уравнения (II. 209).

РИС. 16. Функции F1 (S, X) и — ZdF2u'di

Высокой, этим самым определится порядок верхнего предела зна­чений X. Пусть через скважину отбирается 1 ООО ООО м3 газа в сутки (имеется в виду объем при нормальных условиях); такой расход достаточно высокий. Пусть, далее, вязкость газа р равна 0,01 мПа-с, проницаемость пористой среды k = Ю-12 м2, мощность пласта Н = 10 м, начальное пластовое давление Р = 3 МПа (относительно небольшое давление для столь высокого отбора газа); считаем, что плотность ро соответствует ро = 0,1 МПа. Таким образом, q/р0 — есть заданный объемный расход газа, отбираемого через скважину. Переходя к одинаковым единицам измерения и подставляя при­веденные параметры в выражение для X, получим X ^ 0,04. Стало быть, в реальных случаях параметр X равен 0,01—0,02 и менее.

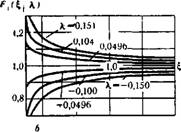
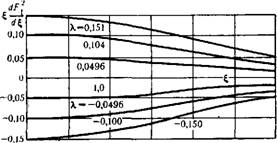
На рис. 16 изображены кривые Fі (S, X), отвечающие несколь­ким значениям параметра X, как положительным, так и отрица­тельным, а также соответствующие кривые — \dF\jd\. Из этих кри­вых видно, что в довольно значительной области вблизи точки \ — 0 (соответственно вблизи $ = Г(Х) для кривых, отвечающи х X < < 0) функция — %dF\id% близка к своему значению при $ = 0 (со­ответственно при с = f(X), т. е. к X. При этом основное изменение функции F\ (£, X), т. е. основное изменение давления газа, сосредо­точивается именно в этой области. При тех же значениях для которых функция — kdFi/dX уже существенно отклоняется от X. функция Fі (£, X) оказывается достаточно близкой к единице - В практически наиболее интересной области значений параметра X, равных по абсолютной величине одной сотой и менее, это свой­ство постоянства функции — \dF\ld\ в области, где Fi (с, X) суще­
ственно отличается от единицы, выражено еще более резко. Обо­значим через £. значение аргумента £, обладающее тем свойством, что при £ < £, значения —XdFl/dX отличаются от X меньше, чем на 0,01 %. Стало быть, при £ < £„ с этой же степенью точности выполняется соотношение

ЈdF?/dЈ = —X; X)-F*(Ј., X) = - XlnЈ/Ј,. (11.215)

Проведенные численные расчеты показывают, что при | X | <0,01 величина Fi(Ј,, X) отличается от единицы менее чем на 0,03, так что при £ > £, справедливо неравенство 0,97<fi(Ј, Х)<1.

Отсюда следует, что с практически вполне достаточной точ­ностью в этой области уравнение (11.209) для функции F\ (£, X) можно заменить линейным относительно F\ (£, X) уравнением

В последнем слагаемом добавлен множитель Fі (;, X), согласно предыдущему, мало отличающийся от единицы. Линейное уравне­ние (11.216) легко интегрируется, в результате получим

XdFbd - = Сехр(— £2/8), (11.217)

Где С—константа интегрирования. Определим эту константу из условия, что при £ = £, величина ldF\№ = —X. Имеем

С ~ — X ехр (— £*/8).

Так как для рассматриваемой практически интересной области |Х|<0,01, значение £* весьма мало (< 0,01) и ехр (—l-8;f) от­личается от единицы не более чем в шестом десятичном знаке, то можно полагать С = — X.

Интегрируя уравнение (11.217), получаем при £ > £.

Fi (£, X) = D — X J £-' ехр (— £2/8) dt (11.218)

Находя константу интегрирования из условия Fi(oo)=l, получим

F\ = 1 — l/2XEi(— 1/8;2). (11.219)

Находя из (11.219) F\ (£,, X) и подставляя в (11.215), получим F? = 1 - 1/2Х Ei(-1/8^)-X In (£/£.). (П.220)

При малых £ имеем асимптотическое выражение Ei (— 1/8£2) = In (TЈ2/8),

Так что

In (£/£,) = 1/2 [Ei (- £2/8) - Ei (- £?/8)].

Подставляя это выражение в (11.220), находим:

F\ = 1 — 1/2Х Ei (— £2/8) (£ < £.). (11.221)

Сравнивая выражения (11.219) и (11.221), видим, что они сов­падают. Отсюда следует весьма существенный вывод о том, что в
практически наиболее интересном интервале значений параметра X | X | < 0,01 функция Fі (S, X) представляется в виде (11.219) при всех значениях I.

Переходя от функции F\ (£, X) к давлению р по формуле (11.208), получаем, что распределение давления с весьма высокой степенью точности представляется для всех значений г и / в виде:

— 0,01<Х= <0,01. (11.222)

Именно таким получилось бы решение задачи, если бы мы заменили в уравнении (II. 206) множитель р в правой части на значение р = Р этого множителя при г = оо, т. е. если бы при тех же граничных и начальных условиях перешли к линейному относи­тельно р2 уравнению

(11.223)

Такой способ линеаризации уравнения (II. 206) был впервые предложен JI. С. Лейбензоном [26]. Приведенные расчеты пока­зывают практически точное совпадение решения расматриваемой нелинейной осесимметричной задачи с решением линеаризован­ной задачи. Успех линеаризации объясняется в данном случае тем, что в случае осесимметричных движений область разбива­ется на две части: 1) область квазистационарного дви­жения, соответствующая малым значениям в которой сосре­доточивается основная часть всего перепада давления, но поток газа почти постоянен, и 2) область малых депрессий (пе­репадов давления), в которой поток газа сравнительно медленно уменьшается, а перепады давлений малы.

В области квазистационарного движения не только разность величин rdp2/dt и 2а2рд (гдр2/дг)/дг равна нулю, как это следует из уравнения (11.206), но и каждая из них сама по себе исчезающе мала (сравнительно со значениями этих величин в тех точках, где они максимальны). Поэтому в этой области поток газа, рав­ный — TzkpoH (\х. р0)-1гдр2/дг, почти постоянен, а значение мно­жителя при втором члене уравнения (11.206) несущественно, и с большой степенью точности можно заменить в этом множителе р (г, t) на Р. В области же малых депрессий, в определенной части которой оба члена уравнения (II.206) существенно отли­чаются от нуля, возможность такой замены обусловливается ма­лостью разности р (г, t) — Р.

Обнаруженная допустимость линеаризации уравнений при опи­сании нелинейных осесимметричных движений вне зависимости от возникающего перепада давления позволяет сделать важные выводы применительно к более общим классам движения. Эти выводы связаны с малостью безразмерного параметра X, — без­размерного расхода — и могут быть в общем виде установлены применением широко известной техники сращиваемых асимпто­тических разложений.

Заметим теперь, что в реальных задачах задается поток газа через скважину, хотя и малого, но конечного фиксированного радиуса, так что граничное условие на скважине имеет вид (II. 206).

Покажем, что построенное выше автомодельное решение удов­летворяет с большой степенью точности этому условию уже спу­стя несколько секунд после начала процесса.

В самом деле, на основании (II. 208) имеем

ГдА = Р2(^ . (П.224)

Дг ] r=R \ dk =

Однако из сказанного выше следует, что при малых X значе­ние функции \dF\ld\ близко к —X при всех не превосходящих нескольких десятых.

При радиусе скважины см, проницаемости k= Ю-12 м2,

Пористости т^0,2, вязкости [х — 0,01 мПа-с величина а2Р = = kP/2my. имеет порядок 103 — 104 см2/с, и тогда уже при / = 3 с

5 = R{a2P()-42 <0,2.

Поэтому можно с весьма высокой степенью точности полагать при t> 3 с

(XdF\/dX%=R(a'P о-1'2 = — X.

Используя это обстоятельство, в соотношении (II. 224) полу­чаем, что спустя несколько секунд после начала движения авто­модельное решение с большой степенью точности удовлетворяет граничному условию (II. 207).

Как было показано, встречающиеся на практике значения па­раметра X по модулю значительно меньше, чем рассмотренное только что, примерно равное — 0,08. Поэтому для меньших X это условие будет удовлетворяться еще быстрее.

Выше было отмечено, что автомодельные решения при X < 0 соответствуют отбору газа из пласта через расширяющуюся со временем скважину. Покажем теперь, что это неестественное, на первый взгляд, свойство решений не препятствует применению их к реальным задачам, поскольку для представляющего практиче­ский интерес времени расширяющаяся (фиктивная) скважина всегда остается внутри настоящей скважины. Для этого определим поря - рядок величины £(Х) — координаты точек подхода кривой F\ (£, X) при Х<0 к оси абсцисс. Как было отмечено, при т. е., в

Частности, при £ = £(Х), функция F\ ($, X) с высокой степенью точности удовлетворяет соотношению

F\(X, X) = - X ln (£/£.).

Полагая £ =Ј(X), Ft (£, X) = 0, получаем

F?(Ј„ X) = X ln (f/?J; l(X) = Ј, exp[x-1F?(Ј„ X)].

При J XI < 0,08, F\ (;„, X) = 0,72, X < 0 значение E. = 0,0050, откуда Ј(X)^ 0,005 е-6-5 = 0,75 • 10~5. Как показывает формула (11.214), промежуток времени Т, за который расширяющаяся внут­ренняя скважина достигает размера настоящей сксажины, составляет

Т = R2(a2l2P)~\

С учетом предыдущих оценок для Г, а2Р и R получим примерно Т ^2 ■ 108 с — около шести лет. Отметим, что значение j X | = 0,08 очень велико сравнительно со значениями, встречающимися на практике. При уменьшении | X | величина Т резко возрастает: так, при X = 0,01 Т = 1075 лет. Таким образом, для реальных задач расширяющаяся (фиктивная) скважина всегда остается внутри настоящей.

Приведенные оценки показывают, что рассматриваемое авто­модельное решение вполне пригодно для реальных задач.

Автомодельность расматриваемой задачи была отмечена Л. С. Лейбензоном и П. Я. Полубариновой-Кочиной. Изложенное решение этой задачи дано Г. И. Баренблаттом.

Задача 1. Пусть проницаемость и пористость пористой среды, плотность и вязкость газа — функции давления. Вводя функцию

P'P'^\kidP' <п-225)

Называемую функцией Лейбензона, привести уравнение движения газа к виду

DP/dt = х(Р)ч*Р. (11.226)

Показать, что при обычных значениях дебитов динамику изменения давления в газовой скважине можно описать, заменяя переменный коэффициент в правой чпсти уравнения * (Р) постоянным х0 = х (Р0), отвечающим начальному значению давления (линеаризация по Л. С. Лейбензону).

Задача 2. В большинстве случаев зависимости параметров пористой среды и газа (жидкости) от давления с дсстаїочной точностью могут быть приближены экспоненциальными функциями (k = k0 m = mcea'"p) и т. д. Показать, что уравнение для давления в этом случае эквивалентно уравнению политропической фильтрации газа

Dp/dt = а2у2р"+1. (11.227)

Задача 3. Используя методы, изложенные в §§ 4 и 5 данной главы, найтн способы определения параметров пласта по кривым изменения давления в газо­вых скважинах.

Задача 4. Рассмотрим уравнение (11.227) для радиально-симметричного движения. Допустим, что начальное давление в пласте пренебрежимо мало, а в начальный момент в скважину быстро закачивается конечное количество жид­кости М («мгновенный источник»), так что искомое решение удовлетворяет ус­ловиям

Оо

Р (г, 0) = 0, f р (г, 0 rdr = м0. (11.228)

0

Показать, что движение автомодельно и соответствующее ему распределение давления дается соотношением

Г / М0 \1/2

= (/2 —52)/12; 0< £ < / = 8; /, = 0, $ > I. (11.229)

Дать обобщение этой постановки и результата на прямолинейно-параллель­ное и сферически-симметричное движения.