ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Нестационарное движение Однородной сжимаемой жидкости. Линейная теория
Постановка основных задач. Простейший и наиболее изученный случай нестационарной фильтрации — движение однородной слабосжимаемой жидкости в упруго деформируемом пласте. Это движение (см. § 1.4) описывается уравнением пьезопро - водности для давления р
Dp/dt = х (д2р/дх2 + д2р! ду2 + d2p! dz2) = *Ьр, (11.83)
По форме совпадающим с классическим уравнением теплопроводности.
Область, в которой ищется распределение давления в жидкости, та же, что рассматривалась для стационарных течений: пористый пласт, часть границ которого непроницаема, а другая часть сообщается с вскрывающими пласт скважинами и соседними пластами.
Граничные условия в задачах линейной нестационарной фильтрации задаются на границах того же типа, что и в задачах напорной стационарной фильтрации: непроницаемых границах, скважинах, галереях, контурах питания. Однако теперь давление, напор или расход, задаваемые на скважинах или галереях, являются, вообще говоря, функциями времени. Часто в модельных задачах задается мгновенное изменение давления или расхода на скважине или галерее от начального до некоторого конечного, что соответствует физически быстрому пуску или закрытию скважины или галереи.
Все принятые обычно варианты граничных условий укладываются в общую форму
{ар + Ьдр/дп) = f(x, у, г, t), а2 + Ь2ф 0; Ыа > 0. (11.84)
Из общей теории уравнения теплопроводности известно, что если на границе области задано условие (11.84), а в начальный момент времени ^=0 условие
Р(х, у, г, 0) = ч(х, у, z), (11.85)
То существует единственное распределение давления р (х, у, г, t), удовлетворяющее уравнению (11.83) и условиям (11.84), (11.85), непрерывное в замкнутой области D, включая границу, на любом конечном интервале времени 0 < t < Т.
Хорошо разработанная техника решения уравнения теплопроводности (см., например, [40]) применима и к задачам теории упругого режима фильтрации. Однако специфика этих задач, связанная с наличием некоторых малых параметров (например, отношение радиуса скважины к расстоянию между скважинами, расстояние между скважинами к расстоянию до контура питания) в ряде случаев существенно упрощает решение.
В типичных условиях нефтяного или газового месторождения или водоносного пласта толщина пласта много меньше его горизонтальной протяженности, что позволяет рассматривать течение как плоскопараллельное. Рассмотрим несколько характерных случаев.
Плоскопараллельное одномерное движение. Пусть скорость течения параллельна оси х не зависит от координат у и z. Давление при этом удовлетворяет уравнению
Dp/dt = %д2рідх2 0 <x<L. (11.85)
Наиболее интересны случаи, для которых в начальный момент времени движение в пласте стационарно. Поскольку стационарное распределение давления также удовлетворяет уравнению (11.86), удобно отсчитывать давление в каждой точке от стационарного значения Р о(х). Таким образом, разность Р = р — Ро удовлетворяет уравнению (11.84) с нулевым начальным условием Р (х, 0) = 0.
Пусть при x=L (на контуре питания) давление сохраняет постоянное значение, равное начальному, а через сечение * = 0 отбирается жидкость, и давление в нем меняется по закону p—f(t). Чтобы получить решение при указанных начальных и краевых условиях, применим преобразование Лапласа, т. е. введем функцию
_________ оо
L {Р (х, /)} = Р (*, а) = J (х, t) dt. (11.87)
|
P(0) = L{f(t)} = F(*y, (П88) Р (L) =0; v2 = о/*, |
О
Для Р получим задачу
D2Pldx2—42P = 0; имеющую решение
Р = F (a) sh [(L — х) v]/sh (Lv). (11.89)
Чтобы перейти от изображения к функции Р (х, t), предположим вначале, что в сечении х = 0 давление мгновенно принимает фиксированное значение Р = ра Ф 0. Тогда F (а) = р°/а.
Р = (/>%») sh[(Z. — *)v]/sh(b). (II.90)
Рассмотрим асимптотику решений при малых временах, чзму, согласно теории преобразования Лапласа, соответствуют большие значения |о|. Выразим в (11.90) гиперболически г функции через
Показательные и, считая 2L "j/"-^-^ 1> разложим это выражение в
Ряд по степеням ехр (—2L\^aU), т. е.
______________ [ оо оо
Р (*. о) = (р°1°) £ ехр (- v (* + 2Ln)) - £ ехр (- v (2L (п + I /1=0 л=0
+ l)-*))l. (11.91)
Производя почленное обращение ряда (11.91), с помощью формул обращения, выведенных, например, в [25], имеем
Оо
Р (х, f) = P° £ jerfc [(2 Ln + х)!2 yVt] — erfc [(2L (n + 1) —
N=0
— x)!2 V%t]}. (11.92)
Ряд (11.92) сходится при всех / и х. Рассмотрим Еначале асимптотику при условии L2/x/> 1. Тогда в выражении для Р (х, і) можно все значения erfc заменить их предельными erfc(oo) = 0,
За исключением члена ряда erfc * _ ■. Имеем
^ 2 Ух*
Р(х, t) = р°етїс[х/2У1й}. (11.93)
Полученнсе решение (II.£3) имеет десякий смысл. С одной стороны, сно спксыЕает ргспределение /аЕхения в пласте конечней дли кы L при махых Еременах v. t<^L2. С другой стороны, оно д;ет распределение давления в пласте бесконечной протяженности L->• -> оо. Любое конечное изменение давления распространяется за заданное время лишь на конечное расстояние и, если рассматриваются ма/ые времена, межно считать пласт бесконечным. Решение (11.93) автомодельно: независимые переменные х и t входят в него лишь в кокбингции x/yVt.
В силу линейности уравнения (11.86) решение для случая произвольного вида функции Р (0, /) = f (і) можно получить с помощью принципа суперпозиции с использованием интеграла Дюамеля
Р(х, t) = I (df(z)/dt)Pi (х, t~x)dt, (11.94)
О
Где Р\(х, і) — решение (11.92) или (11.93) для случая скачкообразного изменения давления при х = 0.
Рассмотрим теперь противоположную асимптотику В этом случае выражение (11.92) неудобно тем, что приходится суммировать много членов ряда. Чтобы получить решение в более удобном виде, можно воспользоваться так называемой второй теоремой разложения для преобразования Лапласа [25], согласно которой регулярная функция F (а), стремящаяся к нулю при | а |->- -> оо, является преобразованием Лапласа функции
3>(/) = ЈRes[F(a)e«], (11.95)
K Ck
Где сумма вычетов берется по всем особым точкам а* функции F (о) в порядке неубывания их модулей. Тогда для F (а), выражаемого формулой (11.90), получим разложение
Pi (х, t) = р°( 1 — x/L) — 2p%t-' s;n [тс (1 — x/L)] exp (— it2xt/L2) - f
+ О [exp (— (4 — є) m2x//L2)]. (11.96)
Из формулы (II. 96) видно, что приближение к стационарному линейному распределению давления происходит экспоненциально, причем характерное время выхода на стационарный режим имеет порядок
Г-2. (11.97)
Для типичных условий фильтрации маловязкой нефти или воды в коллекторах с высокой проницаемостью * имеет порядок 104 см2/с. Тогда из (11.97) следует, что характерное время переходных процессов в малых блоках породы протяженностью 1 м тя0,1 с, при L = 300 м (порядка расстояния между скважинами) т » 3 ч, L = 10 км (порядка размеров месторождения) т = 100 сут и при L=100 км (порядка размеров крупной водонапорной системы) т K 109 с ~ 30 лет. В коллекторах с высоковязкой нефтью и низкой проницаемостью значение х может оказаться на один-два порядка меньше. Тогда соответственно на один-два порядка увеличиваются значения характерных времен.
В практических задачах часто приходится рассматривать нестационарные процессы в сложных системах, в которые входят элементы с различными собственными временами. Оценивая время установления стационарного течения для каждого элемента, мы упростим задачу, отделив те элементы, движение в которых можно считать стационарным, и те, в которых нестационарный процесс находится в начальной стадии.
Плоскорадиальное движение. Рассмотрим одномерное осесимметричное (плоскорадиальное) нестационарное течение, соответствующее нестационарному притоку к одиночной скважине в круговом пласте. Распределение давления определяется как решение уравнения пьезопроводности с радиальной симметрией
Dp/dt = (*/г) д \гдрІдг)Ідг 0<р<л<Я<оо, (II.98)
Удовлетворяющее начальному условию
P(r,0) = f(r) (11.99)
И граничным условиям при г = р и г — R.
Как и выше, в силу линейности уравнения (11.98) можно подразумевать под р только отклонения от стационарного распределения давления р=С} lnr + C2, т. е. считать начальное распределение f (г) = 0.
Переходя в уравнении (11.98) к изображениям по Лапласу, получаем
R-'d [rdp (г, a)ldr]!dr = v2P (г, о), v2 = а/%, (11.100)
Общее решение которого имеет вид
P(r, o) = C, IoM + C2Ko(rv). (11.101)
Где І0 и Ко — модифицированные функции Бесселя от мнимого аргумента нулевого порядка.
Будем искать решения для случая, когда на скважине задается постоянный дебит при всех / > 0. Решение этой задачи используется в наиболее распространенных способах определения параметров пласта по наблюдениям нестационарного притока к скважине. Положим
(2тс&/|л) (гдр/дг) — — q = const или (др/дг)г=р = — = pVр; р (R, t) = 0. (11.102)
Удовлетворяя граничным условиям, получим из (11.101) и (11.102) Р (го) = (p"lpva )[Ко (Я v) Io (rv) — Ко (rv) І0 (Јv)]:
: [I, (pv) Ко (Яv) + Io (flv) Ki (Pv)]. (11.103)
Радиус скважины p обычно равен 10 см или менее. Если расстояние между скважинами R > 300 м, то для типичных условий исследования скважины на нестационарный приток можно применить «промежуточную асимптотику», т. е. положить
Что позволяет упростить выражение (11.103), полагая р]Лз/*С1<^ При этом можно использовать асимптотические формулы для Ко (г), Ki (г), Io (г) и \i(z) при больших и малых значениях аргумента
Io (Z) ^ е2 (21CZ)-1'2, Ко (Z) « е - (ir/22)'/2 2 - со Ко (г) як — ІП (тг/2) 7 = ес 2 0,
Где С = 0,7772 — постоянная Эйлера.
Тогда из (11.103) получим
Р(г, о)= — ро-'КоМ. (11.105)
В частности, для давления в скважине
Р(Р, о) = р'о-1 In (tpv). (11.106)
Отметим важное обстоятельство: соотношение (11.105) не содержит радиус скважины р. Это означает, что в области применимости условия р2/х/ 1 распределение давления не зависит от радиуса скважины. Используя таблицы преобразований Лапласа и связь между преобразованием функции Лапласа и ее производной, получим
Р (г, t)=2-1p'Ei(—r2/4*t). (11.107)
Для давления на скважине с помощью асимптотического выражения Ei (— х) = ln-j-A - при X ОО имеем
Р (р, /) = _ др (4^)-' In (Тр2/4х/) = Q(X (4%kh)~x In (2,25х//Р2), (11.108)
Где Q — полный дебит скважины (q — дебит на единицу толщины пласта). Формулы (11.107) и (11.108) часто используются для определения параметров пласта по данным о нестационарном притоке.
Определение параметров пласта. Общий принцип исследования пластов при нестационарном течении заключается в том, что путем изменения режима эксплуатации скважин в пласте искусственно создается нестационарный режим фильтрации и измеряется давление в зависимости от времени в одной или нескольких скважинах. На основе данных об изменении дебитов и давления, используя решения задач нестационарной фильтрации,
Можно оценить параметры пласта — проницаемость, пьезопровод- ность, расстояния до границ и т. д.
Самым простым и наиболее употребительным способом создания нестационарного течения является временная остановка одной из скважин. Условие ее остановки с момента t0 можно рассматривать как задание на скважине при t>t0 постоянного дебита — Q. Тогда давление на забое остановленной скважины описывается формулой (11.108), определяющей прямую в координатах р. In t. При построении кривой восстановления давления в остановленной скважине асимптотически прямолинейный участок часто устанавливается через непродолжительное время, обычно в первые часы (рис. 5).
Пусть уравнение асимптоты есть р = A In t + В. Сравнение с формулой (11.108) показывает, что А = Q^/iizkn, В —A In (4х/^р2). Поскольку значение Q известно, то после определения по графику параметров А и В можно найти гидропроводность пласта kh/p и отношение х/р2.
Следует учитывать, то радиус скважины в формуле для притока обычно не равен истинному вследствие того, что скважина вскрывает пласт не на всю толщину и не вся поверхность ее открыта для фильтрации жидкости (несовершенство скважины по степени и характеру вскрытия). Кроме того, как было показано в § 1 данной главы, на кажущийся радиус скважины существенно влияет загрязненность призабойной зоны, где проницаемость может быть существенно уменьшенной, или наличие в ней трещин. Поэтому, зная величину х/р2, нельзя по отдельности определить X и р2. Для определения пьезопроводности пласта удобнее использовать метод гидропрослушивания, т. е. исследовать изменение давления в реагирующей скважине, не работавшей к моменту изменения дебита возмущающей скважины. В этом случае характерным размером является не радиус скважин, а расстояние между скважинами, которое известно достаточно точно.
|
РИС. 5. Кривая восстановления давления
'°0 S 10 15 In I |
Для определения пьезопроводности пласта методом гидропрослушивания, если дебит возмущающей скважины изменяется скачком, можно использовать формулу (11.107), записав ее в виде
Ap = p(r, t)-p(r, 0) = = — Q, a (41ГМ)-1 Еі (— г2/4х0,
(11.109)
Где Ар — изменение давления в реагирующей скважине; Q — изменение дебита; г — расстояние реагирующей скважины от возмущающей. Обработка кривых изменения давления в реагирующей скважине заключается в том, что на кривой фиксируется время появления каких-либо
характерных точек. Например, удобно фиксируется точка касания кривой Ар (t) с прямой, проведенной из начала координат. В этой точке (t = 11), как следует из формулы (11.109), r2/4x/i =0,44, откуда х = 0,57г7/ь
Приведенные примеры решения обратных задач для определения параметров пласта ограничены условиями, при которых скважина может рассматриваться как мгновенно пущенный источник постоянной интенсивности в бесконечном однородном пласте. Фактически, когда возмущение, вызванное закрытием скважины, доходит до границ пласта, т. е. через время порядка Q=R2/x, кривая восстановления давления в скважине начинает искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному пластовому давлению. С другой стороны, приток из пласта в скважину, остановленную на устье, не прекращается мгновенно вследствие сжигаемо - сти жидкостей и газов, заполняющих скважину. Время выхода на асимптоту в координатах Ар, In t не должно превышать времени дополнительного притока после остановки. Поэтому возможны условия, особенно в скважинах, расположенных близко от границ пласта, когда прямолиьейного участка на кривой p(\nt) не существует. В связи с этим был предложен ряд способов обработки кривых восстановления давления, учитывающих приток в скважину после ее остановки.
Один из наиболее общих методов обработки кривых восстановления давления был предложен в работе [31]. В этом методе непосредственно используются преобразования Лапласа кривых восстановления давления, вследствие чего он пригоден при произвольном изменении дебита скважин. Такой метод позволяет также в ряде случаев определять по кривым восстановления давления некоторые характеристики неоднородности пласта.
Рассмотрим пласт произвольной конфигурации, в котором при і = 0 начинает эксплуатироваться скважина при нестационарном режиме. Пусть в результате измерений известны зависимости р (р, t)
И -^р ~ __ = q (t). Давление в пласте р(х, у, г, і) удовлетворяет
Уравнению (11.83), а его преобразование по Лапласу Р (х, у, zt а) — уравнению
V2P = 7P/x. (II. 110)
На непроницаемых участках границы справедливо условие дР/дп =0, на контурах питания Р = 0, на скважине P\r=? = Рі{<з). Положим U=~P(x, у, z, о)/Pi (о). Функция U удовлетворяет уравнению (11.110) и однородным условиям на внешних границах пласта (на скважине <7=1). Эта функция не зависит от режима работы скважины. Для преобразования по Лапласу дебита сква-
_ оо
Жины Q(o) = $q (t) имеем
О
Q (a) = 2к (Ш[л) p J e—' (dp/dr)r=Pdt = о
= 2it (kh/p) ?Pi (a) (dViir)r^. (11.111)
Из формулы (11.111) следует, что отношение
T(a) = P,(a)/Q(a) (11.112)
Зависит только от вида функции U, но не от режима эксплуатации скважины. Вид функции ф (а) полностью определяется параметрами пласта. Когда функции pi (t) и q (t) известны, нетрудно численно получить зависимости Pi (а) и Q (а), а отсюда — ф (о). По виду функции ф (а) можно определить некоторые параметры пласта. Рассмотрим простейший пример—скважину в однородном бесконечном пласте. Функция U, как легко получить из формулы (11.105), имеет вид
И = Ко М/Ко (pv), v = уїГх, (11.113)
Откуда
Ф (a) = (2TzkhPdU/dr)-lv. = (2itfcftp)-yKo(pv)/Ki (pv). (11.114)
При практическом построении преобразований Лапласа от функций pi(t) и q(t) удобно перейти к переменной х = 1/a, полагая
Со
Р (х) = J Р (t)e~i/Tdt. Значения х не следует брать меньше 1—2 мин.
О
Поэтому, учитывая порядок * и р, видим, что значения р ]/"а/* = = p/j/хт достаточно малы, чтобы можно было использовать представление функций Ко и Кі для малых значений аргумента. Тогда получим
<F (т) = W (а) = — ц (2itJfeA)-4n (тр/2 У*?) = = p. (irM)-1 In х + [і^ісАЛ)-1 ln(4x/T2P2). (11.115)
Параметры пласта — коэффициенты в формуле (11.115) — определяются по графику ¥ (In t) точно так же, как и по графику р (In t) при мгновенной остановке скважины. То, что зависимость ¥(1пх) прямолинейна, позволяет ограничиться вычислением интегралов при трех — четырех значениях х.
Описанный общий подход позволяет получать методом восстановления давления некоторые параметры неоднородного пласта.
Рассмотрим пример. Пусть скважина радиусом р расположена в центре круговой зоны радиуса R в бесконечном пласте. Проницаемость зоны k\ и пьезопроводность *i отличаются от проницаемости k2 и пьезопроводности *2 во внешней зоне пласта. Функция Г(г) для этого случая может быть получена с использованием решения вида (11.101) и асимптотических формул (11.104). При этом для p2/xi< х < R2/%i функция W (х) асимптотически выражается формулой (11.115) при k = k\ х==*і, а для х > R2U2 имеем
ЦТ (х) = !л(4тсМ)"11п X + |Л (4nk2h)~l In (4x2/f2p*2), (11.116)
Где эквивалентный радиус скважины о* тот же, что и для стационарного притока (см. 11.19):
Р' = Я(р/Я)т = р(р/#)7-1, т = (11.117)
Сравнивая формулы (11.115) и (11.116), видим, что формула (11.117) описывает преобразованную кривую восстановления давления в скважине радиуса р* в однородном пласте с параметрами внешней зоны. Точно так же можно показать, что эквивалентный радиус скважины, определяемый по данным о нестационарном притоке при горизонтальных или вертикальных трещинах, таков же, как и определяемый для стационарного течения при тех же условиях. Из этого примера видно, что исследование скважин методом восстановления давления позволяет определить степень загрязнения призабойной зоны и оценить эффективность работ по интенсификации притока.
Описанный метод обработки кривых восстановления давления можно использовать и для определения других параметров неоднородности пласта: расстояния до непроницаемого или проводящего экрана, радиуса трещин и т. д.
Метод интегральных соотношений. Хорошо разработанная теория уравнений математической физики позволяет получить в принципе точные решения широкого класса задач нестационарной фильтрации. Однако эти решения не всегда удовлетворяют требованиям простоты и обозримости. Учитывая недостаточную точность исходных данных в задачах фильтрации, связанных с движением жидкостей и газов в природных пластах, часто можно удовлетвориться простыми приближенными, легко обозримыми решениями.
Возможность успешного применения приближенных методов в теории нестационарной фильтрации связана со следующими особенностями рассматриваемых задач. Во-первых, большинство задач нестационарной фильтрации однородной жидкости сводится к решению уравнений параболического типа, для которых характерно сглаживание начальных возмущений искомых величин со временем и по мере продвижения внутрь области от источника возмущений. Во-вторых, в ряде задач, представляющих практический интерес, искомое решение имеет в некоторых точках области (скважины, галереи) известные особенности. При этом в основной части области состояние системы близко к невозмущенному. Наконец, в большинстве случаев существенны лишь интегральные характеристики решения.
В ряде приближенных методов используется понятие области влияния или области возмущения, вне которой течение можно считать невозмущенным, т. е. сохраняются начальные значения р или и. Возможность введения такой области следует из анализа точных решений, приведенных в настоящем параграфе. Например, из формулы (11.93) следует, что отклонение от начального убывает с ростом х как ехр(—x2/4*t). Одним из наиболее общих приближенных методов в теории фильтрации является метод интегральных соотношений [3].
Сущность его заключается в том, что исходное дифференциальное уравнение (11.86 ) или (11.98) в области возмущения скважины заменяется системой интегральных соотношений вида
Lf]dp/dtfi(x, t)dx = xL()d2p/dx2fi(x, t)dx, і = 0, 1, ..., п, (11.118) МО £•.(')
Где fi(x, t), і = 0, 1, . . ., n образуют полную систему как функции от х на отрезке [L\ (/), L2(t)j. Если р(х, t), представить в виде разложения в ряд по функциям Д (х, і), то из (11.118) получим систему уравнений для коэффициентов этого ряда.
Рассмотрим задачу о возмущении первоначального стационарного движения в пласте. Возьмем простейшую систему функций — последовательные степени пространственной переменной
1, X, X , ..., X, ...
Пусть в момент t — 0 происходит отбор жидкости из пласта с расходом — kb/pHG. Давление в этом случае распределено по линейному закону
Р (х, 0) = Р + Gx. (II. 119)
Будем искать приближенное решение задачи в виде многочлена р(х, t) = P0 (t) + Pi(t)x/l+, ..., +Pn(t)x"/l" (0 <*</),
Р (х, T) = р (х, 0) (х > I). (11.120)
В таком виде задача имеет п+2 неизвестных: Рі (і) и l{t). Для их определения можно составить систему уравнений, состоящую из некоторого числа интегральных соотношений, граничного условия при х — 0 и условия при X = /. При х — I должны выполняться условия непрерывности давления р (/, t) = Р + GI и некоторой степени гладкости функции р (х, t):
Dp (I, t)/dx = д2р (I, t)lдх2 = ... =dkp (I, t)ldxk = 0.
Выбор наилучшего приближенного метода расчета р (х, t) связан с тем, насколько удачно подобрано число используемых интегральных соотношений и условий гладкости.
В рассматриваемом случае
Р(0, t) = px, р(х, 0) = р0 = 0. (II.121)
Используя интегрирование по частям и теорему о дифференцировании определенного интеграла, приведем систему (11.118) к виду
(ИЛ22>
±\pxdx = *p(0, 0. (11.123)
J 'fpx*dx =*xk(k — 1) lfpxk-2dx, k>2. (II. 124)
О 0
|
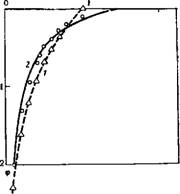
{-х/2Ул7 РИС. 6. К задаче о нестационарном притоке к галерее: О — нулевое приближение: 1 — первое приближение: 2 — точное решение |
РИС. 7. Зависимость безразмерного давления от безразмерной координаты для осесим - метричного течения. Решения: 1 — приближенное: 2 — точное
При п = 1 из (11.122) следует
I = 2 Vxt, и (О, t) = —k (др/дх)!^ = k(pi— /?о)/2[л V^t. (II. 125)
Напомним, что при точном решении по формуле (11.93) получим
«о (0, t) = k{px—pQ)l]x V™t - (11.126)
Заметим, что решение для п — 1 совпадает с тем, которое получается по известному методу последовательной смены стационарных состояний [44].
Для второго приближения (п = 2) используем снова соотношение (11.122) и условие
(др/дх)хы-о = 0, (11.127)
Что дает
Р(х, t) = рі{\—хЛ)2, /2=12х/. (11.128)
Для скорости фильтрации при х = 0 получим
И (0, t) = k(pi — poVVS^t, (11.129)
Что близко к точному решению (11.126). Если во втором приближении вместо (11.127) использовать интегральное соотношение (11.122), то вид решения не изменится.
Если для третьего приближения (п — 3) использовать соотношения (11.122), (11.123) и (11.127), то третье приближение совпадает со вторым. Если же использовать первые три интегральных соотношения без условия (11.127), то получим (опуская промежуточные выкладки)
Р(х, t) = px(\— 0,583С + 0,107С2 + 0,0061 С3), С = х/У%Г. (11.130)
|
2 і |
На рис. 6 приведено сопоставление полученных приближенных решений с точными. При построении приближений более высокого порядка возникают трудности, обусловленные тем, что отсутствуют сколько-нибудь обоснованные правила выбора
Наилучшего из нескольких дополнительных условий. Кроме того, при этом приходится строить приближения функций с помощью многочленов высокого порядка. Впрочем, основная цель построения приближенных решений — получение простых аналитических зависимостей — достигается уже приближениями второго порядка.
Рассмотрим без подробных выкладок осесимметричную задачу о пуске скважин с заданным дебитом q в бесконечном пласте. Решение уравнения (11.98) ищется в виде
Р (г, t) = q In (r/l) + P0 + P1 (r/l) +, ..., +Pn (r/l)", (П.131)
Где 1(f)— переменный радиус зоны возмущения. Система интегральных соотношений имеет вид
±'\пгр(г, t)dr=-xq, (11.132) 'о
Jt Р (г> 0 dr = 1{\р (г - 0 rk~~4r (k>\). (11.133) о о
В нулевом приближении (Ро = Pi = ... =0) имеем единственную неизвестную функцию / (/), которая определяется из уравнения (11.132): _ _
1 = 2 Vа*/, р0(г, t) = q In (r!2 Vxt). (11.134)
С использованием уравнений (11.132), (11.133) и условий непрерывности р и др/дг (т. е. р = 0 и дрідг = 0) при г = l(t) получим первое приближение в виде
I = /Ш, р = q In (r/УШй) —q + qr/УШ. (11.135)
При сопоставлении приближенных решений 1 с точным 2 (рис. 7) имеем, что даже результаты расчета по формуле (11.134) и тем более по формуле (11.135) довольно хорошо согласуются с точным решением.
Метод интегральных соотношений позволяет с удовлетворительной точностью получить простые приближенные решения задач о притоке к скважинам в ограниченном пласте. Соответствующие точные решения получаются в виде плохо сходящихся рядов Фурье — Бесселя и трудно обозримы. Ограничимся здесь одним примером.
Рассмотрим круговой пласт радиуса R, на контуре которого поддерживается постоянное давление, равное начальному (принимаемому за нуль). В начальный момент производится пуск скважины пренебрежимо малого радиуса, расположенной в центре пласта. Тогда вплоть до момента / = t\ = R2H2xt в первом приближении справедливо представление (11.135). При t > ti необходимо учитывать условие на контуре
P(R, 0 = 0. (11.136)
Используя снова первое приближение разложения (11.131) и полагая l(t) = R, получим с учетом (11.136)
Р (г, t) = q In (r/R) + Ро (0 (1 —r/R). (11.137)
Тогда из первого интегрального соотношения (11.132) получим
Jt]p(r, = |я2^° = -*/>0. (11.138)
О
Уравнение (11.138) следует решить при условии непрерывности давления при tsztь Ро !<=/,=— Я - Решение имеет вид
P0(t) = — <?ехр[— 6*(/ — /,)/Я2]. (11.139)
Таким образом, будем иметь приближенное выражение для распределения давления
Р(г, 0 = <7 In (г/Я) — <7(1 — г/Я) ехр [— 6*(/ — /і)/Я2]. (11.140)
Как видно, распределение давления экспоненциально стремится к стационарному.