ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Эффекты диффузии и неравновесности в задачах вытеснения нефти раствором активной примеси
Так же, как и в «обычной» теории двухфазной фильтрации (см. гл. IV), крупномасштабное приближение оказывается недостаточным там, где возникают области больших локальных градиентов основных переменных, т. е. вблизи скачков насыщенности и концентрации, а также в гетерогенных (трещиновато-пористых и слоисто - неоднородных) пластах. Анализ возникающих при этом ситуаций с учетом диссипативных-капиллярных и диффузионных эффектов является ключевым для понимания механизмов, формирующих нефтеотдачу в реальных пластах. В данном параграфе кратко рассмотрены некоторые из них.
Тонкая структура сопряженного скачка концентрации активной примеси и насыщенности. Выпишем систему уравнений одномерного вытеснения нефти раствором активной примеси в пренебрежении ее влиянием на плотности фаз, но с учетом диссипативных эффектов; примесь будем считать водорастворимой:
£ (msc + а) + и £ (cF) + е £ (сФЯ) = v £ (D д£);
F = filfi+V-ifi/V2]-1; S = P, sS,* + P, cC, x; Ф = ^2- (V.98)
Параметры є и v характеризуют отношения капиллярного давления к полному гидродинамическому перепаду давления в пласте и отношение времени переноса частицы фильтрационным потоком
ко времени диффузии вдоль пласта и обычно малы (см. гл. IV и гл. V). Если положить s = v = 0, то придем к рассмотренной выше задаче крупномасштабного приближения. Пренебрежение малыми параметрами незаконно вблизи скачков внешнего (крупномасштабного) приближения. При малых є и v анализ решения в окрестности скачков сводится к построению (по аналогии с тем, как мы это делали уже не раз) внутреннего решения задачи. При этом новые элементы появляются лишь при рассмотрении тонкой структуры сопряженных (s, с) скачков, чем мы и ограничимся здесь.
Перейдем в уравнениях (V.98) к системе координат, движущейся вместе со скачком, введя «быстрые» переменные
Ч = (* — vt)/e, Т = t/в, (V.99)
И будем искать нетривиальное стационарное решение, удовлетворяющее условиям сращивания с внешним решением: s(+co) = s+, с(±оо) = с±. При этом предполагается, что величины V, s±, с± определены при построении глобального внешнего решения (см. гл. V) и, в частности, удовлетворяют условиям на скачке (V.51), (V.52), (V.53).
Для искомого стационарного решения s (13), с (у) из (V.98) с учетом условий (V.51) — (V.52) имеем систему
Ds/d-q = —Н (с) [В (s, с) V (s, с) + (с — с~) 1 (с)]/С (s, с), dc/d-q = Н (с) (с — с ) Z (с), Z = F~~ Е/ [s~ + (а — а-)/т (с — с-)]; {/ = mV/U, (V. 100) Y — F — F~ — (s — s~); H = eVfrD; G = P, JP. C; В = vD/гФР^.
Системе (V.100) на фазовой плоскости (s, с) соответствует уравнение
= _ G (s, с) (с - е-) z (с) v
Ds l(c — с~) Z (с) + В (s, с) Y (s, с)]*
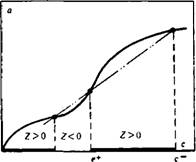
Особыми точками этого уравнения являются точки М +(s+, с+) и М~ (s~~, с~); искомому решению внутренней задачи отвечает траектория, соединяющая эти особые точки. Услов ия существования внутреннего решения тесно связаны с условиями устойчивости скачка во внешнем решении, хотя и не сводятся к ним. Покажем это на одном примере (остальные случаи допускают аналогичное рассмотрение). Будем рассматривать структуру скачка «полезной» активной примеси, когда в скачке возрастают концентрация примеси и насыщенность. Будем полагать также, что примесь уменьшает межфазное натяжение и капиллярное давление. Тогда в соответствии с построениями рис. 66 имеем для точек M—(s~, с~) и Af+(s+, с+)
Z ■ = dF = с~) < F (s~ с~)
' ds s - + ЛА/Лс ^ s~+ А~ '
-р—^<«/ = дг<—%—• ~ • (V-102)
На плоскости (s, с) линиям F = F (s, с+) и F = F (s, с~) соответствуют горизонтальные прямые с = с±, а прямой М~Л1+ — кривая Y = О, касающаяся прямой с = с - в точке М-.
Величина Y положительна под кривой М+М~М* и отрицательна над ней. Вдоль М+М~М* имеем из (V.101):
Dc/ds = — G (s, с) = —Р, S/P, с < 0.
Функция Z(c) обращается в нуль (рис. 67) при с = с+; она положительна для тех с, для которых
[а (с) — а (с-)] (с — с-)"1 > [а (с+) — а (с-)] (с+ — с-)-1. (V. 103)
В дальнейшем будем предполагать, что условие (V.103) выполняется при с+<с<с~. На роль, которую это условие играет при построении тонкой структуры скачка, указал А. Ф. Зазовский. С учетом принятых допущений В < 0, и знаменатель в правой части уравнения (V.101) обращается в нуль при Z> 0, Y > 0, т. е. изоклина бесконечности dc/ds—со, лежит вне криволинейного треугольника М+М~М* (см. рис. 66). В этом случае поле направлений в фазовой плоскости уравнения (V.101) принимает вид, показанный на рис. 66, и существует единственная траектория М+М~, соединяющая особые точки Л4+ и М~. Более детальный анализ показывает, что траектория М+М~ является сепаратрисой седла М+, принадлежащей пучку траекторий, входящих в седло-узел М~. Асимптотика решения вблизи особых точек устанавливается при помощи известной техники, причем оказывается, что вблизи точек М+ и М~, соответственно
C—C+ —k(s — s+), k > О,
С — С------ с+ ехр [R/(s — s—)] (s — s~)~2, s< sr,
|
РИС. 67. К определению знака z (с)
|
R = 2СГ - {s~ + A-)}lB~F7ss > 0. (V.104)
Интегрируя уравнения (V.100) и используя асимптотические соотношения (V.104), находим
S—S~~2G~lB~H~F~uq, С —С - — const lj-2 exp (—Х~тд), "Q - і------------------- ОО,
S — s+ — const exp (—x+-q), с — с+ ~~ const exp (—х+1з)>
Xі = % - «/ (s± + = - £ . (V.105)
Последние выражения показывают, что ширина переходной зоны (—1 /Xі) обратно пропорциональна скорости скачка и тем меньше, чем больше разница между характеристическими скоростями второго семейства характеристик и скоростью скачка.
Существенно также, что за скачком изменение концентрации происходит экспоненциальным образом, а насыщенности—степенным, т. е. значительно медленнее. Если попытаться построить внутреннее решение типа равномерно распространяющейся волны при а с = const (так называемый контактный разрыв, когда скорость скачка равна характеристической скорости во всем диапазоне изменения концентрации примеси в скачке), то окажется, что такого решения нет. Построение внутреннего решения в таком случае требует более тонких рассуждений. Решение это имеет вид расширяющейся пропорционально tU2 переходной зоны (наподобие тепловой волны).
Заметим, что построение внутреннего решения существенно использует условие (V.103), в силу которого в полосе с+<с<с~нет особых точек уравнения (V.101). По-видимому, это условие следует рассматривать как дополнительное необходимое условие устойчивости скачка.
Неравновесные эффекты в структуре сопряженного скачка. В задачах вытеснения нефти раствором активной примеси возникает новый важный источник неравновесности — нарушение равновесия в распределении активной примеси между водой, нефтью и пористым скелетом, а также между отдельными компонентами гетерогенной пористой среды. Связанные с этим эффекты проанализируем вновь на простейшей ситуации — задаче вытеснения водорастворимой полезной примеси в пренебрежении капиллярными эффектами и диффузией в направлении потока.
Имеем задачу
Dms. ., dF (s, с) „ д (msc + а) UdcF _______ „
~дГ + и дх = U' dt г ~дГ ~ и'
Da/dt = х-1? (с, а) ? (с, а* (с)) = О, (V.106)
S (х, 0) = so, с (х, 0) = со, s (t, 0) = s°, с (і, 0) = с0, а (х, 0) = а* (с0).
Отношение времени установления равновесного распределения примеси к времени движения жидкости в пласте играет в последующем рассмотрении роль малого параметра задачи. Внешнее решение задачи остается прежним. Чтобы построить внутреннее решение, перейдем к подвижной системе координат: у = (х — Vt)ltV\ t'— tft, и будем искать стационарное распределение s = s(-q), с = = с(тз). При этом имеем
F — f, s = F+ — ijS+ = F~~ XjS - = const, cF — (cs 4- Л) = c±F± — Е,- (c±s± + Л±) = const,
Da/d-q = —9 (а, с) (Л = aim). (V. 107)
Выражая из первых двух соотношений (V.107) а через с, имеем линейную связь между этими величинами:
А = а+ + 1Тхт (с — с+) {F+ — E/S+), (V. 108)
С = с+ + 6/ (a — а+) (F+ —
При этом связь между у и а определяется интегрированием уравнения (V.107)
Ч = Лиг (УЛ09)
Для интерпретации этого результата удобно воспользоваться (с, а)-диаграммой (см. рис. 58).
Нетрудно видеть, что равновесная изотерма сорбции а = а* (с) разбивает первый квадрант плоскости (с, а) на две части; над этой кривой <р < 0, под ней <р > 0. Интегрирование (V.109) происходит по прямой, соединяющей точки (с+, а+) и (с-, а~), так что при очевидных допущениях f положительно вдоль пути интегрирования и обращается в нуль в крайних точках. При этом - q изменяется от —оо до оо. Стационарное распределение концентрации, определяемое выражением (V.109), в физических координатах имеет эффективную толщину, пропорциональную xV, и, таким образом, расширяется с увеличением скорости вытеснения. Соответствующий профиль насыщенности однозначно определяется из первых соотношений (V.107). Полученное решение определяет главный член поправки к крупномасштабному решению, вносимой неравновесностью сорбции. Согласно ему неравновесность сорбции сказывается на динамике нефтеотдачи, но не на ее конечном значении. Эффекты, связанные с конечной нефтеотдачей, требуют анализа следующих членов разложения.
Капиллярная пропитка. Как уже говорилось в гл. IV, одним из важнейших цроцессов, формирующих нефтеотдачу гетерогенных пластов, является капиллярная пропитка — впитывание воды в малопроницаемые пропластки и блоки породы, первоначально заполненные нефтью. Поэтому важно знать, как влияет на эти процессы наличие в воде активной примеси, влияющей на фазовые проницаемости и капиллярное давление. Рассмотрим здесь лишь основной процесс одномерной противоточной капиллярной пропитки, характеризующейся равенством нулю суммарного потока фаз. Описание этого процесса дается системой (V.98), в которой следует положить (/ = 0. Имеем задачу:
Ds. д Г Ffz /п ds, п дс \"1 _
Д [msc + а (с)] dt
S (X, 0) = So. С (x, 0) = Co, s(0, i) — s°, c(0, 0 = c°.
Сформулированная задача, как легко видеть из соображений размерности, имеет, подобно задаче обычной капиллярной пропитки, автомодельное решение вида
S=5(S), с = С(5), X = х(е<)-1/2,
(V.111)
Где функции 5(£) и С (Е) — решение задачи
D lrYds 1 »vdc\ _i_ d nDdc\ , 5 d (mcs + a)
|
FJl 1*2 |
|
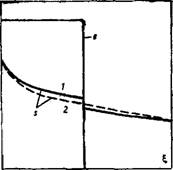
РИС. 68. Распределение концентрации с активной примеси и насыщенности s при капиллярной пропитке: 1-Р. с+ 0; 2-Я, с = О |
|
"-Ш + |
|
^2» (V.112) |
|
Ij-2 |
|
= 0. |
|
Di |
Ж ГЛ Ті + Ті) + di ("Г di) + "2
Характер этого решения определяющим образом зависит от соотношения капиллярного и диффузионного коэффициентов переноса. Ограничимся здесь случаем, когда диффузионный перенос мал, что отвечает обычному соотношению параметров. При этом, полагая в (V.112) £> = 0 и вычитая из второго уравнения первое, умноженное на с, получим
Таким образом, перенос концентрации примеси описывается уравнением первого порядка, которое допускает разрывные решения (в частности, концентрация примеси может переноситься в виде «ступеньки»). При этом, поскольку в силу первого уравнения (V. 110) капиллярное давление на скачке непрерывно, скачок концентрации сопровождается скачком насыщенности из условия
Р (s+, с+) = Р (s-, с~). (V. 114)
Условие баланса насыщенности, следующее из лэрвого уравнения (V.110), определяет связь между скоростью скачка, величиной скачка насыщенности и скачками производных s, и с
Типичная картина решения показана на рис. 68. Характерно отставание фронта примеси от фронта воды. Это свойство имеет важные последствия. Поскольку ведущий механизм — капиллярная пропитка чистой водой, наличие активной примеси слабо влияет на скорость пропитки. В этих условиях основной эффект активной примеси может быть связан лишь с ее влиянием на неснижаемую нефтенасыщенность (1—s°). Ясно, что на этот показатель и следует
обращать внимание при подборе агента воздействия при заводнении гетерогенных пластов с гидрофильными блоками.
Иная картина получается, если блоки первоначально гидрофобны и пропитка их водой невозможна. В этом случае принципиального улучшения показателей процесса можно достичь, добавив к воде гидрофилизующий реагент (ПАВ), делающий поверхность породы гидрофильной. Можно показать, что в таком случае скорость процесса определяется опережающей диффузией химреагента, который ведет за собой пропитку. Этот вывод также существен для правильного выбора гидрофилизирующих реагентов.
[1] Это следует из того, что квадратичная форма пропорциональная
Удельной работе сил взаимодействия жидкости с пористой средой, не должна Зависеть от выбора системы координат.
[2] Сказанное не относится к нефти, находящейся в контакте с природным газом. В этом случае при повышении давления увеличивается количество растворенного в нефти газа, и ее вязкость заметно падает.
[3] В этом параграфе для сокращения записи используется оператор вектор* ного дифференцирования набла: ytp = grad у, ya = div«.
[4] См. также [47, 6, 12, 44].
[5] Действительно, в данном случае можно было бы вместо напора h ввести пропорциональное ему давление у подошвы пласта hpg, что не отразилось бы на остальных выкладках.
[6] Математически это является следствием того, что для уравнения (11.147) справедлив принцип максимума, в соответствии с которым решение не может оказаться отрицательным при положительных начальном и граничном условиях.
[7] Читатель, знакомый с методом сращиваемых асимптотических разложений, легко заметит, что речь идет, по существу, о построении внутреннего решения задачи, отвечающего структуре фронта. Нетрудно проделать соответствующие формальные рассуждения.
[8] Приводимые в этом параграфе данные численных расчетов получены в ИПМ АН СССР Ф. Д. Турецкой.
[9] См. также [9, 19, 41].
[10] Нетрудно понять, что поскольку на поверхности целика градиент давления должен быть направлен вдоль нее, соотношение (IV. 170) верно с точностью до членов порядка (Vftp р)2/| ур\2. Поэтому совершаемая ошибка тем меньше, чем более пологой является искомая поверхность.