Двигатели стирлинга

ДИНАМИКА МАШИНЫ

В технической литературе, посвященной тепловым двигате­лям, обычно основное внимание уделяется термодинамическим и тепловым аспектам работы и конструкции двигателя и прак­тически не рассматривается динамика машины; монографии, по­священные двигателям Стирлинга, не являются исключением в этом смысле. В качестве механизма привода в обычных тепло­вых двигателях с возвратно-поступательным движением почти всегда применяются кривошипно-шатунные механизмы, в то время как в двигателях Стирлинга применяются самые различ­ные механизмы привода (рис. 1.27). Поэтому следует уделить должное внимание динамике и кинематике механизмов привода двигателя Стирлинга. Подробное описание механики и дина­мики механизмов, применяющихся в двигателе Стирлинга, по­требовало бы много места; мы ограничимся лишь рассмотре­нием некоторых специфических особенностей, с которыми при­дется столкнуться.

Следует, например, обязательно рассмотреть вопрос о ба­лансировке двигателя, поскольку существует неверное представ­ление, будто бы все двигатели Стирлинга отлично сбалансиро­ваны и не испытывают вибраций. На самом деле это не так, и при использовании кривошипно-шатунного механизма для дви­гателя Стирлинга проблема балансировки может быть сложнее, чем для двигателя внутреннего сгорания. Отсутствие в двига­теле Стирлинга периодических внутренних взрывов означает, что один источник вибрации устранен, но это не должно на­страивать на благодушный лад конструктора механизма при­вода. На элементы конструкции двигателя Стирлинга действуют различные силы, но при решении задачи о балансировке двига­теля рассматривается сила, обусловленная перемещением по­движных частей, т. е. сила инерции.

На тела или, в частности, на любые элементы конструкции двигателя, которые участвуют в ускоренном пли замедленном движении, действует сила, которая передается на основание; следовательно, эта сила нежелательна. К сожалению, данная проблема возникает в любом двигателе с возвратно-поступа­тельным движением, будь то двигатель Стирлинга или двига­тель внутреннего сгорания, поскольку поршень должен остано­виться в верхней мертвой точке, затем разогнаться до макси­мальной скорости, замедлиться и вновь остановиться в нижней мертвой точке; далее цикл повторяется. Связанный с поршнем шток также участвует в аналогичном движении, хотя обычно движение представляют в виде суммы возвратно-поступатель­ного и вращательного движений.

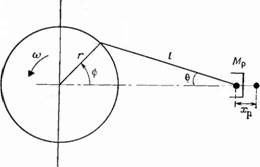
Сила инерции определяется как произведение массы рас­сматриваемого элемента конструкции на его ускорение [46]. Для идеальной балансировки необходимо, чтобы сумма всех сил инерции была равна нулю. Более того, это условие должно выполняться при любых рабочих скоростях двигателя. Если сумма сил не равна нулю, то получается результирующая, пли остаточная, сила, называемая силой разбаланса. Хотя при низ­ких скоростях можно допустить небольшую силу разбаланса, при высоких скоростях она становится очень большой, так как растет пропорционально квадрату скорости и будет переда­ваться не только на крепежные детали двигателя, в которых могут возникать сильные вибрации, но и на подшипники дви­гателя, которые могут выйти из строя или их срок службы сильно сократится. Чтобы попять практические особенности за­дачи, рассмотрим основной кривошипно-шатунный механизм. Обращаясь к рис. 2.25, находим силу инерции поршня Fpr.

Fpi — МрХр, (2.59)

Где хр — ускорение поршня. Из геометрических соображений по­лучаем хр = /"(1 — cos Ф) + /(1 — cos 6) и п sin 6 = sin Ф, где П — 1/г и, следовательно, хр можно выразить через угол пово­рота кривошипа ф соотношением

Хр = г (1 - cos Ф) + I [1 - (1 - sin2 Ф/И2)9-5]. (2.60)

Дважды дифференцируя соотношение (2.60), находим выраже­ние для ускорения

2 Г. , и2 cos 20 + Sin4 0 П /QR14

Хотя это выражение является строгим математическим соотно­шением, удобнее выразить ускорение поршня в виде ряда по возрастающим степеням одной тригонометрической функции — угла поворота кривошипа. Это позволяет легко определить от­дельные гармоники и рассматривать их независимо друг от друга. Другими словами, соотношение для Хр удобнее предста-

Вить в виде ряда Фурье [47], и это можно сделать, разлагая член (1 — sin2 ф/п2)0-5 по теореме бинома:

Л. I sin20 . sin4<Ј. sin6Ф /г.

*р = г (1 - cos Ф + + -^3- + - Jg-J-} , (2.62)

И для случая постоянной скорости вращения вала ю () получаем

Icp = со2/ (cos Ф + л cos 2ф + В cos 4ф + С cos 6«jb + ...), (2.63)

_J_ , J_______ . 15 . . _________________ 1_____

Где л — n н- 4/гз -+- 128n5 -t- ...; Ts— 4/гз l6rt5

С = —!__ I———u

Ь 12 /г5 ^ 512 п7 ^ ------------------

Важно иметь в виду, что эта сила действует только по линии хода двигателя. Следовательно, если рассматривается четырех­цилиндровый двигатель, то вдоль линии хода каждого цилинд­ра будет действовать своя сила, т. е. в итоге действуют четыре силы. Цель «балансировки» двигателя — свести сумму этих сил к нулю или по крайней мере сделать ее как можно меньшей; кроме того, необходимо добиться, чтобы сумма моментов этих сил относительно оси двигателя также была равна нулю, или сделать ее по крайней мере как можно меньше.

Форма соотношения (2.63) показывает, что сила, которую нужно сбалансировать, имеет составляющую, изменяющуюся со скоростью вращения вала кривошипа, которая суммируется с бесконечным рядом четных гармоник скорости вращения вала. Проблему балансировки часто сильно упрощают как из теоре­тических, так и из практических соображений, рассматривая только силу, изменяющуюся синхронно со скоростью вращения вала кривошипа (так называемую первичную силу ты2г Cos ф), И силу, изменяющуюся синхронно с удвоенной скоростью вра­щения вала (так называемую вторичную силу тю2гЛ cos 2ф). Это упрощение не слишком грубое, поскольку при балансировке

1

Этих двух сил часто балансируются и высшие гармоники или их большая часть.

Итак, практическая задача состоит в том, чтобы сбаланси­ровать первичную и вторичную силы, а также первичный и вто­ричный моменты, обусловленные этими силами. Моменты или пары сил приходится рассматривать только для двигателей с двумя и более цилиндрами. Силы инерции отдельных движу­щихся возвратно-поступательно элементов конструкции много­цилиндрового двигателя не всегда действуют в плоскости, про­ходящей через центр тяжести двигателя, и, поскольку линии действия сил проходят на некотором расстоянии от центра тя­жести, создаются соответствующие моменты. Если сумма этих моментов не равна нулю, то будут возникать вибрации. На основании приведенных выше соображений с помощью соотно­шений (2.63) и (2.59) можно получить приближенное выраже­ние для силы инерции поршня, совершающего возвратно-посту­пательное движение:

FP! = тр(£>2г (cos ф + cos 2Ф/п). (2.64)

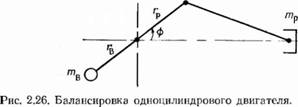
Рассмотрим задачу балансировки одноцилиндрового двига­теля с кривошипно-шатунным приводом (рис. 2.26). Очевидным решением задачи является применение балансирующего проти­вовеса, вращающегося относительно оси кривошипа и создаю­щего силу инерции, равную по величине, но противоположную

По направлению силе инерции поршня:

ТрГрИ2 cos Ф + твгвсО2 cos (ф + я) = X! Fx, (2.65)

Если трГр — твГв, то £ Fx = 0.

Таким образом, сила, возникающая при возвратно-поступа­тельном движении, полностью уравновешивается с помощью противовеса, подвешенного на расстоянии гв от оси, и для на­правления х действительно так и обстоит дело. Однако, хотя поршень движется только по оси х, вращающийся противовес движется как в направлении х, так и в направлении у. При полной балансировке сила, действующая в направлении у, так­же должна быть равна нулю, но это условие не достигается: на самом деле величина этой силы равна

Fy = /пвгвсо2 sin Ф. (2.66)

Следовательно, мы всего лишь изменили направление дей­ствия первичной силы на 90°. Задача осталась практически не решенной еще и потому, что вращающийся противовес не ока­зал вообще никакого влияния ни на вторичную силу (силу 2ф), нп на высшие гармоники. Итак, одноцилиндровый двигатель с крнвошипно-шатунным приводным механизмом нельзя сбалан­сировать при помощи вращающегося противовеса, и, следова­тельно, нужно искать иные методы сведения к нулю силы инерции.

В многоцилиндровом двигателе можно уравновесить силы, создаваемые одним из цилиндров, силами, создаваемыми дру­гим цилиндром, например если их кривошипы будут вращаться в протпвофазе (со сдвигом фаз на 180°). Действительно, такой способ позволяет для рядного двигателя с шестью цилиндрами сбалансировать как первичные, так и вторичные силы и, кроме того, существенно уменьшить первичные и вторичные моменты. Следовательно, ключом к решению проблемы балансировки дви­гателя является уравновешивание сил инерции одного цилиндра силами инерции другого цилиндра.

Теперь рассмотрим, как применяются эти концепции теории балансировки к двигателям Стирлинга, и покажем это на при­мере трех основных типов механизма привода двигателя — крн - вошппно-шатунного, ромбического (для одноцилиндрового дви­гателя), с косой шайбой. Если кривошипы парных цилиндров в рядном двигателе вращаются в нротивофазе, то первичные силы и вторичные моменты уравновешиваются, но вторичные силы и первичные моменты не балансируются. Обычно такая ситуация допустима, но, к сожалению, с точки зрения балан­сировки наиболее предпочтителен режим работы двигателя Стирлинга со сдвигом фазы около 90°, что при использовании кривошипно-шатунного механизма для двигателя модификации альфа требует сдвига фазы кривошипа 90°. Первичные силы будут действовать под углом 90° относительно друг друга и, следовательно, не будут взаимно компенсироваться. Даже если применить противовес, то, как мы уже видели, баланс первич­ных сил не будет достигаться. Однако две вторичные силы бу­дут уравновешены, поскольку угол между ними равен 2-90° = = 180е, так что они равны по величине и противоположны по направлению. Вторичные моменты не будут уравновешены, по­скольку они действуют в одном и том же направлении относи­тельно оси двигателя. Аналогичное положение создается и для двигателя модификации гамма. Двухцилиндровый двигатель — самый сложный случай с точки зрения балансировки, и на заре развития железнодорожного транспорта инженерам было чрезвычайно трудно решить задачу балансировки, когда они кон­струировали двухтактные паровые двигатели с двумя цилинд­рами. Они пытались уменьшить разбаланс, добавляя противо­весы на колеса, но это приводило лишь к снижению силы инер­ции в одном направлении за счет увеличения ее в направлении, перпендикулярном первому. Следовательно, заметного успеха в балансировке двухцилиндрового двигателя Стирлинга с рядным расположением двигателей не достигнуто. Это не исключает применения кривошнпно-шатунного механизма в двигателях Стирлинга, но рекомендуется использовать многоцилиндровую систему, чтобы облегчить задачу балансировки. Для оценки ба­лансировочных характеристик разрабатываемого двигателя не требуется большого количества подробных данных, так как основные проблемы можно быстро решить теоретически. Чтобы проиллюстрировать методику решения этой задачи, рассмотрим хорошо документированный двигатель 4L23 фирм «Дженерал моторе» и «Филипс» [48].