Детали машин

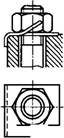
Теория винтовой пары

Зависимость между моментом, приложенным к гайке, и осевой силой винта. Если винт нагружен осевой силой F (рис. 1.13), то для завинчивания гайки к ключу необходимо приложить момент Т^ъ, а к стержню винта — реактивный момент Гр, который удерживает стержень от вращения. При этом можно записать

ГзаВ=Гт+Гр, (1.3)

Где Тт — момент сил трения на опорном торце гайки; Гр — момент сил трения в резьбе. Равенство (1.3), так же как и последующие зависимости, справедливо для любых винтовых пар болтов, винтов, шпилек и винтовых механизмов.

Не допуская существенной погрешности, принимают приведен­ный радиус сил трения на опорном торце гайки равным среднему радиусу этого торца, или Аф/2. При этом

TT=Ff(DJ2),

Где DCp = (Z>i + *4Tb)/2; Dx —наружный диаметр опорного торца гай­ки; dOTB — диаметр отверстия под винт; /— коэффициент трения на торце гайки.

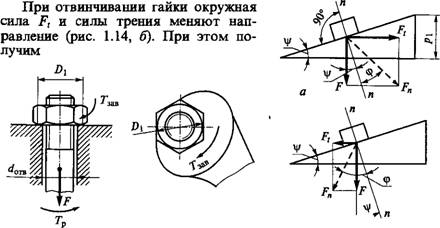
Момент сил трения в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плос­кости (рис. 1.14, а). По известной теореме механики, учитывающей силы трения, ползун находится в равновесии, если равнодейству­ющая F„ системы внешних сил отклонена от нормали п — п на угол трения (р. В нашем случае внешними являются осевая сила F и окру­жная сила Ft = 2TJd2. Здесь Гр — не реактивный, а активный момент со стороны ключа, равный T^—Tj [см. формулу (1.3)].

Далее (рис. 1.14) Ft=F tg(^ + <p) или

Tp = 0,5Fd2tg(<P + <p),

Где ф — угол подъема резьбы [по формуле (1.1)]; (p = a.rctgfnp — угол трения в резьбе; /щ, — приведенный коэффициент трения в резьбе, учитывающий влияние угла профиля [формула (1.2)].

Подставляя (1.4) и (1.5) в формулу (1.3), найдем искомую зави­симость:

F,=Ftg((p-il/).

Момент отвинчивания с учетом трения на торце гайки, по аналогии с формулой (1.6),

Тот* = 0,5 Fd2 [(DJd2)f+ Tg (q> - ф)].

Полученные зависимости позволяют отметить:

1. По формуле (1.6) можно подсчитать отношение осевой силы винта F к силе FT, приложенной на ручке ключа, т. е. F/Fn которое дает выигрыш в силе. Для стандартных метрических резьб при стандартной длине ключа L&L5DИ/«0,15 F/Fz = 70...80 (см. табл. 1.6).

2. Стержень винта не только растягивается силой F, но и закру­чивается моментом Гр.

Самоторможение и КПД винтовой пары. Условие самоторможе­ния можно записать в виде Готв> 0, где Готв определяется по формуле (1.8). Рассматривая самоторможение только в резьбе без учета трения на торце гайки, получим Tg((P — J/)>0 или

Ф«Р-

Для крепежных резьб угол подъема ф лежит в пределах 2°30'...3°30', а угол трения (р изменяется в зависимости от коэф­фициента трения в пределах от 6 (при/«0,1) до 16° (при/»0,3). Таким образом, все крепежные резьбы — самотормозящие. В вин­товых механизмах резьбы выполняют как самотормозящими, так и несамотормозящими.

Приведенные выше величины коэффициента трения, свидетель­ствующие о значительных запасах самоторможения, справедливы только при статических нагрузках. При переменных нагрузках и осо­бенно при вибрациях вследствие взаимных микросмещений поверх­ностей трения (например, в результате радиальных упругих дефор­маций гайки и стержня винта) коэффициент трения существенно снижается (до 0,02 и ниже). Условие самоторможения нарушается. Происходит самоотвинчивание.

КПД Y винтовой пары представляет интерес главным образом для винтовых механизмов. Его можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отноше­ние работ равно отношению моментов Т^в/Тшв, в котором

Определяется по формуле (1.6), а — по той же формуле, но при /= 0 и ф = 0:

Ц=7YaB/r3aB=tgM(A*/<0/+ tg (ф+cp)]. (1.10)

Учитьшая потери только в резьбе (Гх=0), найдем КПД собствен­но винтовой пары:

Г1^ёф/[1ё(ф + ср)]. (1.11)

В самотормозящей паре, где ф<ср, у <0,5. Так как большинство винтовых механизмов самотормозящие, то их КПД меньше 0,5.

Формула (1.11) позволяет отметить, что rj возрастает с увеличе­нием ф и уменьшением ср.

Для увеличения угла подъема резьбы ф в винтовых механизмах применяют многозаходные винты. В практике редко используют винты, у которых ф больше 20...25°, так как дальнейший прирост КПД незначителен, а изготовление резьбы затруднено. Кроме того, при большом ф становится малым выигрыш в силе или передаточ­ное отношение винтовой пары (см. гл. 14).

Для повышения КПД винтовых механизмов используют также различные средства, понижающие трение в резьбе: антифрикцион­ные металлы, тщательную обработку и смазку трущихся поверх­ностей, установку подшипников под гайку или упорный торец вин­та, применение шариковых винтовых пар и пр.

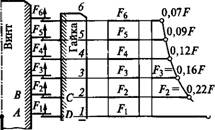
Распределение осевой нагрузки винта по виткам резьбы. На рис. 1.15 изображена схема винтовой пары. Осевая нагрузка винта пере­дается через резьбу гайке и уравновешивается реакцией ее опоры. Каждый виток резьбы нагружается соответственно силами Fu F2, ...

..., FZ9 где Z — число витков резьбы гайки.

2

Сумма F - В общем случае Ft не равны между собой. Задача 1

О распределении нагрузки по виткам статически неопределима. Для ее решения уравнения равновесия дополняют уравнениями дефор­маций. Впервые она была решена Н. Е. Жуковским в 1902 г. Не излагая это сравнительно сложное решение, ограничиваемся качест­венной оценкой причин неравномерного распределения нагрузки. В первом приближении полагаем, что стержень винта и гайка абсолютно жесткие, а витки резьбы податливые. Тогда после при­ложения нагрузки F все точки стержня винта (например, А и В) Сместятся одинаково относительно соответствующих точек гайки (например, С и D). Все витки получат равные прогибы, а следова­тельно, и равные нагрузки (рис. 1.15, а). Во втором приближении полагаем стержень винта упругим, а гайку оставляем жесткой. Тогда относительное перемещение точек А и D будет больше от­носительного перемещения точек В и С на величину растяжения стержня на участке АВ. Так как нагрузка витков пропорциональна их прогибу или относительному перемещению соответствующих точек, то нагрузка первого витка больше второго и т. д.

В действительности все элементы винтовой пары по­датливы, только винт растя­гивается, а гайка сжимается. Перемещения точки D мень­ше перемещений точки С на величину сжатия гайки на участке CD. Сжатие гайки дополнительно увеличит раз­ность относительных пере­мещений точек А и D, В и Сит. д., а следовательно,

И неравномерность нагрузки витков резьбы.

Все изложенное можно записать с помощью математических символов. Обозначим А^, Ав, Дс, AD перемещения соответствующих точек. Вследствие растяжения участка АВ винта АВ<АА, а вследст­вие сжатия участка CD гайки AD<AC.

Относительное перемещение точек А и D, В и С

Aad = Aa-Ad, Авс=Ав-Ас.

Учитывая предыдущие неравенства, находим AAd>ABC- Следова­тельно, нагрузка первого витка больше нагрузки второго и т. д.

График распределения нагрузки по виткам, полученный на ос­нове решения системы уравнений для стандартной шестивитковой гайки высотой #=0,8rf, изображен на рис. 1.15, б. В дальнейшем решение Н. Е. Жуковского было подтверждено экспериментальны­ми исследованиями на прозрачных моделях. График свидетельству­ет о значительной перегрузке нижних витков и нецелесообразности увеличения числа витков гайки, так как последние витки мало нагружены.

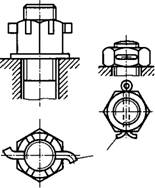
Теоретические и экспериментальные исследования позволили разработать конструкции специальных гаек, выравнивающих рас­пределение нагрузки в резьбе (рис. 1.16). На рис. 1.16, а изображена так называемая висячая гайка. Выравнивания нагрузки в резьбе здесь достигают тем, что как винт, так и гайка растягиваются. При этом неравенство AD<AC изменится на обратное AD>AC, а разность Aad—Авс уменьшится. Кроме того, в наиболее нагруженной нижней зоне висячая гайка тоньше и обладает повышенной податливостью, что также способствует выравниванию нагрузки в резьбе. На рис. 1.16, б показана разновидность висячей гайки — гайка с кольцевой выточкой, У гайки, изображенной на рис. 1.16, в, срезаны вершины нижних витков резьбы под углом 15...20°. При этом увеличивается прогиб нижних витков винта, так как они соприкасаются с гайкой
не всей поверхностью, а только своими вершина­ми. Увеличение прогиба витков снижает нагрузку этих витков.

Специальные гайки осо­бенно желательно приме­нять для соединений, под­вергающихся действию пе­ременных нагрузок. Раз­рушение таких соедине­ний носит усталостный характер и происходит в зоне наибольшей концентрации напряже­ний у нижнего (наиболее нагруженного) витка резьбы. Опытом установлено, что применение специальных гаек позволяет повысить динамическую прочность резьбовых соединений на 20...30%.

Решение, результаты которого приведены на рис. 1.15, б, спра­ведливо в пределах упругих деформаций и при номинальных раз­мерах. Вследствие большой жесткости резьбы на фактическое рас­пределение нагрузки существенно влияют технологические отклоне­ния размеров; небольшие пластические деформации перегруженных витков, допустимые для крепежных резьб; приработка резьб. По­этому при практических расчетах неравномерность распределения нагрузки по виткам резьбы учитывают опытным коэффициентом Кт (см. ниже).