Детали машин

Разновидности волновых передач, их оценка и применение

Разработано большое число разновидностей волновых передач: с коротким гибким колесом (рис. 10.13), герметичные (рис. 10.14), винтовые (рис. 10.15), с электромагнитным генератором (рис. 10.16) и др.

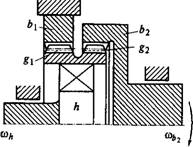
В передачах с коротким гибким колесом первая ступень работает так же, как в основном типе волновой передачи, а вторая ступень может увеличивать передаточное отношение или выполнять роль зубчатого волнового соединения гибкого колеса с выходным валом.

Первый вариант позволяет получить очень большие передаточ­ные отношения, но имеет низкий КПД и не получил распростране­ния.

Второй вариант получает все большее распространение наряду с основным типом передачи.

% I

8 B h

Iz

Рис. 10.14

В волновом соединении Zg2=Zb2 (часто вьшолняют Zgl =Zg2). Гео­метрия зубчатого зацепления этого соединения имеет свои особен­ности, которые здесь не рассматриваются (см. [17]).

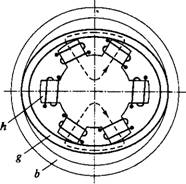
Герметичная передача передает движение через герметичную стенку, разделяющую пространства А и 2>. Глухой гибкий стакан с гибким фланцем герметично закрепляют на стенке (например, приваривают). Зубчатый венец располагают в средней части стака­на. Ни одна другая передача не может так просто решать эту задачу. Такая передача находит применение в химической, атомной, космической и других областях техники.

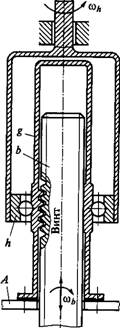
Винтовая передача преобразует вращательное движение в посту­пательное. Ее применяют преимущественно в герметичном исполне­нии.

Передача с электромагнитным генератором сочетает функции двигателя и передачи. Здесь волновое деформирование гибкого колеса осуществляют вращающимся электромагнитным полем. Не­подвижный генератор имеет ряд электромагнитов (полюсов). С по­мощью специального устройства электромагниты включают по­очередно. Магнитный поток замыкается через гибкое колесо и де­формирует его в соответствующих местах. Основное достоинство передачи — весьма малая инерционность. Здесь вращается только гибкое колесо. Вращение медленное, а масса небольшая. Малая инерционность существенна для следящих и других подобных си­стем. Отрицательное свойство передачи — низкий КПД (в извест­ных конструкциях не более 6...8%).

На основе изложенного можно отметить следующие основные качества волновых передач.

1. Большое передаточное отношение. В одной ступени можно получить I до 300, а в специальных передачах — до нескольких десятков тысяч.

2. Большое число зубьев в одновременном зацеплении. Напри­мер, при /=100 одновременно зацепляются до 60...80 пар зубьев вместо 1...2 пары в обычных передачах. Как следствие этого, высо-

Кая нагрузочная способность при ма­лых габаритах и массе. В некоторых конструкциях масса составляет поло­вину, а объем — 1/3 от обычной плане­тарной передачи.

3. Уменьшение кинематической по­грешности вследствие двухзонности и многопарности зацепления. Извест - Рис. 10.15 ны передачи с кинематической погреш­

Ностью, не более 0,5...1,0 угл. мин.

4. При одинаковых передаточных отношениях КПД волновых передач близок к КПД планетарных и многоступенчатых простых передач (например, до 0,9 при /= 100).

5. Малые нагрузки на валы и опоры вследствие симметричности конструкции.

6. Возможность передачи движения в герметизированное про­странство (через герметичную стенку).

7. Малая инерционность при специальном исполнении.

8. Меньше шум.

9. Подобно планетарной передаче она может быть использована не только как редуктор или мультипликатор, но и как дифференци­альный механизм.

10. Конструкции волновых передач не вызывают особых тех­нологических трудностей при их изготовлении.

11. Число деталей меньше в несколько раз, а стоимость — при­мерно в два раза. Срок службы стандартных передач общего назна­чения 10000 ч.

К недостаткам современных конструкций волновых передач можно отнести: сравнительно большую величину нижнего предела передаточного отношения 4iiii~80; сравнительную сложность
изготовления гибкого колеса и генератора волн (требуется специ­альная оснастка). Это затрудняет индивидуальное производство и ремонтные работы.

Применять волновые передачи целесообразно в механизмах с большим передаточным отношением, а также в устройствах со специальными требованиями к герметичности, кинематической точ­ности, инерционности и пр.

Параметры оптимизации волновой передачи:

1. Форма и размер деформирования гибкого колеса.

2. Геометрия зацепления — высота зубьев, коэффициенты сме­щения xg и хъ (по условию отсутствия интерференции зубьев под нагрузкой).

3. Коэффициент ширины зубчатого венца

4. Коэффициент толщины зубчатого венца j/sd по условию мак­симума коэффициента запаса сопротивлению усталости sa.

Пример расчета 10.1. Рассчитать волновой редуктор общего назначения: I%G= 100, Rih=1450 мин" Т2=800 Н м=800 ■ 103 Н * мм, срок службы 10 000 ч, нагрузка близка к постоянной.

Решение. 1. По формуле (10.12) находим zg—200, г^=202. Выбираем зубья с широкой впадиной (см. рис. 10.8). По рекомендациям к формулам (10.37) и (10.41) принимаем: Yz=L,3, ^=0,16, ^=0,012, sa = ,l, ^ = 1,9, материал гибкого коле­са— 30ХГСА, 28...32 HRC с последующим дробеструйным наклепом, = =480 МПа, £=2,1 • 105 МПа. По формуле (10.41),

0,456* 800 103

Согласуя с наружным диаметром гибкого подшипника (см. табл. 10.1), при­нимаем dx=D=160 мм. Находим Ь = фь^х =0,16' 160«25 мм, 5 = ^^ = 0,012' 160« «2 мм.

Учитывая, что величины dxn dg близкие, получаем m=dg/zgtt 160/200=0,8 мм — согласуется со стандартом (см. таол. 10.2).

2. Рассчитываем геометрию зубьев гибкого колеса. Диаметр окружности впадин Dfg=dx+2S= 164 мм. Подбираем zg и xg, обеспечивающие такой dfg.

Нарезаем червячной фрезой с уменьшенной высотой головки зуба инструмента AJq = 0,35, а коэффициент высоты головки зуба колеса h*=0.

По формуле (10.27) и рекомендации (10.25) принимаем xg=0 И уточняем zg:zg = = 164/0,8+ 2 0,35 = 205,7. Принимаем zg = 206. При этом /^ = 206/2=103. Отклонение + 3% —допустимо ±4%. По той же формуле уточняем xg=dfgj{2m)—0,5Zg+А ^ = = 164/(2• 0,8)—0,5• 206-H0,35=—0,15 — в рекомендуемых пределах. По формуле (10.25), высота зуба hg= 1,35 • 0,8 = 1,08 мм. По формуле (10.29), диаметр окружности вершин зубьев dag= 164+2* 1,08 = 166,16 мм.

3. По рекомендации (10.26) принимаем W0/M = 1,2, при этом и>0 = 0,96 мм.

4. Выполняем проверочный расчет прочности гибкого колеса. По формуле (10.37), гт/в=1,5 1,3 2,1 Ю5 2 0,96/812 = 120 МПа, где r=dJ2+5/2 = S0 + =S мм. По формулам (10.38) и (10.39), <7pe=<7pm=0,45'800'103/(160 25 2) = 45 МПа.

По формуле (10.40), тв=тт = 800' 103/(4тг 812 2)=4,85 МПа. Отмечаем малую величину напряжений кручения, которую в дальнейшем не учитываем.

По формуле (10.42), при Ка = 1,9, 0,15 [см. (15.6)] и <хв=<7/в+<хрд= 165 МПа <*т = 0рт = 45 МПа, 5^=480/(1,9* 165-1-0,15 * 45)= 1,5 = [5Г]« 1,5. Условие прочности со­блюдается.

Однако возможно, что принятая толщина 5 не является оптимальной. Для выяснения этого повторяют проверочные расчеты. Задаваясь несколькими вели­чинами <5, меньшими и большими принятой (например, <5= 1,8 мм, 5=2,2 мм), строят график sa и по максимуму sa уточняют <5. Обучающимся рекомендуется самим провести такой поиск.

5. Рассчитываем геометрию жесткого колеса R^=Zg4-2=206+2=208. Его нареза­ют долбяком с полной высотой зуба при высоте зуба жесткого колеса, уменьшенной на один модуль.

По формуле (10.23), хь= -0,15-(0,8-0,96)/0,8 = 0,05.

По табл. 10.2 принимаем долбяк: г<)=80, 4ю = 66,64 мм; AJj = L,35, х0 = 0,3. По 0,05-0,3

Формуле (10.32), InvaHfl=2----------- Tg 20°+ 0,014904=0,013482 или ано = 19022'. По

208-80

Формуле (10.31), Дно=0»8 (208—80) Cos 20°/(2 Cos 19°22') = 51 мм. По формуле (10.28), ^=2(51 +0,5 -66,64)= 168,64 мм.

По второй формуле (10.30), принимая Hj=M=0,8 мм, находим = 166,16 + +2 0,96-2 0,8 = 166,48 мм.

6. Проверяем отсутствие интерференции по переходным кривым. Для этого определяем диаметры граничных точек. Для гибкого колеса по формуле (10.35), принимая PQ=Q,2, находим

Tg а/=Tg 20 - 4 (0,35 - 0,2+0,15)/(206 Sin 40°)=0,3549

Или а/= 19°32'.

По формуле (10.34), dlg=0,8 206 Cos 20°/Cos 19°32' = 164,32 мм. По неравенству (10.30), 166,48 >164,32 + 2 0,96= 166,24 — условие соблюдается.

Для жесткого колеса: по формуле (10.36), Cos «^=0,8 80 Cos 20°/66,64 = 0,9025, или аао=25°Г12"; Tga/=Tgl9O22'+80(Tg25T12'/-Tgl9°22')/208 = 0,39582, или ос/= =21°35'42" и £^=0,8 '208 Cos 20°/Cos 21°35'42" = 168,17 мм.

По неравенству (10.29), 166,16< 168,17-2 0,96 = 166,25 мм — неравенство соб­людается.