Детали машин

Расчет прочности зубьев

Основные критерии работоспособности и расчета. Червячные пе­редачи, так же как и зубчатые, рассчитывают по напряжениям изгиба и контактным напряжениям. В отличие от зубчатых в чер­вячных передачах чаще наблюдается износ и заедание, а не выкра­шивание поверхности зубьев. При мягком материале колеса (оло­вянные бронзы) заедание проявляется в так называемом постепен­ном «намазывании» бронзы на червяк, при котором передача может еще работать продолжительное время. При твердых материалах (алюминиево-железистые бронзы, чугун и т. п.) заедание переходит в задир поверхности с последующим быстрым разрушением зубьев колеса.

Повышенный износ и заедание червячных передач связаны с боль­шими скоростями скольжения и неблагоприятным направлением скольжения относительно линии контакта.

Из теории смазки (см. гл. 16) известно, что наиболее благоприятным условием для образования жидкостного трения является перпендикулярное направление ско­рости скольжения (рис. 9.8) к линии контакта (ф = 90°). В этом случае масло затягива­ется под тело А. Между трущимися телами (А и Б) образуется непрерывный масляный слой; сухое трение металлов заменяется жидкостным. При направлении скорости скольжения вдоль линии контакта (ф =0) масляный слой в контактной зоне образоваться не может; здесь будет сухое и полусухое трение. Чем меньше угол ф, Тем меньше возможность образования жидкостного трения.

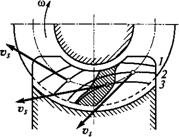
Последовательное расположение контактных линий (1, 2, 3...) в процессе зацепле­ния червячной пары показано на рис. 9.9. Там же показаны скорости скольжения, направление которых близко к направлению окружной скорости червяка [см. рис. 9.6 и формулу (9.11)]. В заштрихованной зоне направление Vs почти совпадает с направ­лением контактных линий; условия смазки здесь затруднены. Поэтому при больших нагрузках в этой зоне начинается заедание, которое распространяется на всю рабо­чую поверхность зуба.

.Смазка

У//Ш//Ш///ШЖ Б

Для предупреждения заедания ограничивают контактные напря­жения и применяют специальные антифрикционные пары матери­алов: червяк — сталь, колесо — бронза или чугун. Устранение за­едания в червячных передачах не устраняет абразивного износа зубьев. Интенсивность износа зависит также от величины контакт­ных напряжений. Поэтому расчет по контактным напряжениям для червячных передач является основным. Расчет по напряжениям изгиба производится при этом как проверочный. Только при мелко­модульных колесах с большим числом зубьев (Z2> 100) напряжения изгиба могут оказаться решающими. Расчет по напряжениям изги­ба выполняют как основной для передач ручных приводов.

Расчет на прочность по контактным напряжениям. Основное урав­нение (8.2)

<Тя=0,418^9Ар/Р»р

Применяют и для червячного зацепления. Для архимедовых чер­вяков радиус кривизны витков червяка в осевом сечении рх = оо. При этом по формуле (8.9) с учетом уравнения (8.21) находим

L/Pnp«2cos2 Yl(D2 sin а).

По аналогии с косозубой передачей, удельная нагрузка для червячных передач

Бп Кн БаКн 2Т2Кн

9ч=—- =

K cosa cosy d2d Деа£ cosa

Где k=di5ea{;/cosy — суммарная длина контактной линии (см. рис. 9.5); ea=l,8...2,2— торцовый коэффициент перекрытия в средней
плоскости червячного колеса; £«0,75 — коэффициент, учитыва­ющий уменьшение длины контактной линии в связи с тем, что соприкосновение осуществляется не по полной дуге обхвата (25), А так, как показано на рис. 9.9. После подстановки в формулу (9.18) найдем

Л/ d^d^E^ sin 2а

Приближенно при а=20° и х=0 [38]

Еа = (V0,03zi+z2 + l - 0,1 7Z2 + 2,9)/2,95. (9.20)

Для проектного расчета формулу (9.19) решают относительно D2, Заменяя Dl=Qm=Qd2/Z2 и принимая а=20°; Кн& 1,1, у«10°, 25а «100°«1,75 рад, ва=1,8, £«0,75.

При этом D2 = 1,25 V-^f". (9.21)

V (y/zi)

Учитывая flw=0,5rf2 (Q/Z2 +1), (9.22)

Решаем формулу (9.21) относительно межосевого расстояния:

3 I £пр?2

Aw = 0,625 (?/z2+1) ?/r-57h - (9-23)

В формулах (9.19)...(9.23) £,пр = 2£1£2/(£1+ ^2), где ^ и ^ — моду­ли упругости материалов червяка и колеса соответственно; /?] = =2,1 • 105 МПа — сталь; £2=0,9-105 МПа — бронза, чугун.

При проектном расчете отношением Q/Z2 задаются. При этом учитывают следующее. Неравномерность распределения нагруз­ки в зацеплении существенно зависит от прогиба червяка. В свою очередь, этот прогиб зависит от диаметра червяка и расстоя­ния между опорами. Диаметр червяка пропорционален Q, а рас­стояние между опорами пропорционально диаметру колеса или z2 (см. рис. 9.2). Поэтому при больших z2 следует принимать боль­шие Q.

Однако при увеличении Q уменьшаются у и КПД [см. формулы (9.1) и (9.12)], а также увеличиваются габариты передачи. Для силовых передач принимают Q/Z2=0,22...0,4.

Расчет на прочность по напряжениям изгиба. По напряжениям изгиба рассчитывают только зубья колеса, так как витки червяка по форме и материалу значительно прочнее зубьев колеса. Точный расчет напряжений изгиба усложняется переменной формой сече­ния зуба по ширине колеса и тем, что основание зуба расположено не по прямой линии, а по дуге окружности (см. рис. 9.5). В приб­лиженных расчетах червячное колесо рассматривают как косозу - бое. При этом в формулу (8.32) вводят следующие поправки и упро­щения.

1. По своей форме зуб червячного колеса прочнее зуба ко­созубого колеса (примерно на 40%). Это связано с дуговой формой зуба и с тем, что во всех сечениях, кроме среднего, зуб червячного колеса нарезается как бы с положительным смещением. Особен­ности формы зуба червячных колес учитывает коэффициент формы зуба Yf:

Zv............ 20 24 26 28 30 32 35 37 40 45 50

Yf........... 1,98 1,88 1,85 1,80 1,76 1,71 1,64 1,61 1,55 1,48 1,45

Z„ ........... 60 80 100 150 300

Yf........... 1,40 1,34 1,30 1,27 1,24

2. Червячная пара сравнительно хорошо прирабатывается. По­этому принимают KF(X= 1 и Yp= 1 [см. формулу (8.34)] и, далее,

7F/,= l/(6aO=l/(l,8 0,75) = 0,74.

При этом формулу (8.32) можно записать в виде

^=0,74У (9.24)

Ь2т„

Где KF — коэффициент расчетной нагрузки (см. ниже); Mn=Mcosy; Yf — см. выше с учетом эквивалентного числа зубьев колеса

Zw=z2/cos3y. (9.25)

Расчетная нагрузка. Для червячных передач приближенно прини­мают

KH=KF=KJCfr

Где ^ — коэффициент динамической нагрузки; Кр — коэффициент концентрации нагрузки.

Как было отмечено выше, одним из достоинств червячной пе­редачи является плавность и бесшумность работы. Поэтому дина­мические нагрузки в этих передачах невелики. При достаточно высокой точности изготовления принимают 1 при м/с;

При Vs>3 м/с.

Хорошая прирабатываемость материалов червячной пары уме­ньшает неравномерность нагрузки по контактным линиям. При постоянной внешней нагрузке Кр= 1; при переменной нагруз­ке в проектировочных расчетах 1,05... 1,2 — большие величи­ны при малых Q и больших z2 с последующим уточнением по формуле

Где 0 — коэффициент деформации червяка (табл. 9.4); X — коэф­фициент режима нагрузки передачи.

Если переменный режим нагрузки задан циклограммой (см. рис. 8.41), то X— 2 (иА)]- Здесь Th Nh U — вращающий мо­

Мент на колесе, частота вращения колеса и время работы при й нагрузке соответственно; Т^ — номинальный (максимальный из длительно действующих) вращающий момент.

Для типовых режимов нагружения (рис. 8.42) величина X приве­дена в табл. 9.5.