Детали машин

Проверочный расчет валов

Выбор расчетной схемы и определение расчетных нагрузок. Расчет валов базируют на тех разделах курса сопротивления материалов, в которых рассматривают неоднородное напряженное состояние и расчет при переменных напряжениях. При этом действительные условия работы вала заменяют условными и приводят к одной из известных расчетных схем. При переходе от конструкции к расчет­ной схеме производят схематизацию нагрузок, опор и формы вала. Вследствие такой схематизации расчет валов становится прибли­женным.

Напомним, что в расчетных схемах используют три основных типа опор: шарнирно-неподвижную, шарнирно-подвижную, защем­ление или заделку. Защемление применяют иногда в опорах непо­движных осей. Для вращающихся осей и валов защемление не допускают.

Выбирая тип расчетной опоры, необходимо учитывать, что де - формативные перемещения валов обычно весьма малы, и если конструкция действительной опоры допускает хотя бы неболь­шой поворот или перемещение, то этого достаточно, чтобы считать ее шарнирной или подвижной. При этих условиях подшипники, одновременно воспринимающие осевые и радиальные нагрузки, заменяют шарнирно-неподвижными опорами, а подшипники, во­спринимающие только радиальные нагрузки,— шарнирно-подви - жными.

Условимся в дальнейшем все рассуждения иллюстрировать при­мером расчета вала, изображенного на рис. 15.1. Для этого вала,
учитывая наклон зуба шестерни и направление момента Т, левую опору заменяем шарнирно-неподвижной, а правую — шарнирно - подвижной опорами (рис. 15.3).

Действительные нагрузки не являются сосредоточенными, они распределены по длине ступицы, ширине подшипника и т. п. Расчет­ные нагрузки рассматривают обычно как сосредоточенные. В на­шем примере (см. рис. 15.1) вал нагружен силами Ft, Fa и Fr (см. рис. 8.28), действующими в полюсе зацепления (рис. 15.3, а), и моментом Г на полумуфте. В гл. 17 показано, что большинство муфт вследст­вие неизбежной несоосности соединяемых валов нагружают вал дополнительной силой FM. Примеры определения FM для некоторых типов муфт даны в той же главе.

При расчете валов приближенно можно принимать FF=(0,2...0,5)FtF, где FTM —

Окружная сила на муфте или как FMtt25YpT—для входных валов редукторов

И выходных валов одноступенчатых редукторов; FM& 250 у/т— для выходных ва­лов многоступенчатых редукторов. Здесь Т — в [Нм]. Последние

Формулы учитывают, что в общем Кг

Случае на конце вала может быть „ ^L*_

Установлена не только муфта, а ше - JS Fa 1

Стерня, звездочка или шкив. R

ГМ

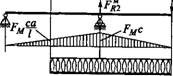
Из приведенной на рис. 15.3, а расчетной схемы вид­но, что векторы сил Fr и Fa расположены в вертикаль­ной плоскости (в плоскости чертежа рис. 15.1 или рис. 15.3), а вектор окружной си­лы Ft — в горизонтальной плоскости. Вектор силы FM Расположен в плоскости сме­щения рассчитываемого и присоединяемого к нему ва­лов. Положение этой плоско­сти на стадии расчетов опре­делить невозможно, оно мо­жет быть любым, так как зависит от случайных неточ­ностей монтажа. В связи с этим расчетную схему вала по рис. 15.3, а целесообразно представить в виде трех от­дельных схем — см. рис. 15.3, Б, в, г, где Ft, Fr и Fa приведены

Гмп

^^.р Oh

^niiiBLj

IT»»-

Ризонтальная плоскость

«1

К оси вала. На рис. 15.3, б изгибающий момент Ma=Fa-Djl, а на рис. 15.3, д вращающий момент T=Ft- Dx2 (в сечении I — I) явля­ются результатом такого приведения. Здесь Dx — делительный диа­метр шестерни.

Под каждой из трех расчетных схем построены эпюры изгиба­ющих моментов, действующих в трех указанных выше плоскостях. По этим эпюрам легко определить суммарные изгибающие момен­ты в любом сечении вала.

Так, например, рассматривая случай нагружения сечения I — I максимальным изгибающим моментом (худший случай), можно записать:

Ab a ab ca

MwpT=Fr- + Ma~; MTOV^FtMm=Fm~.

Расчет на прочность. На практике установлено, что для ва­лов основным видом разрушения является усталостное. Статиче­ское разрушение наблюдается значительно реже. Оно происхо­дит под действием случайных кратковременных перегрузок. Поэ­тому для валов расчет на сопротивление усталости является основ­ным. Расчет на статическую прочность выполняют как провероч­ный.

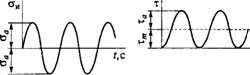
При расчете на сопротивление усталости необходимо прежде всего установить характер цикла напряжений. Вследствие вращения вала напряжения изгиба в различных точках его поперечного сече­ния изменяются по симметричному циклу, даже при постоянной нагрузке (исключение составляют случаи, когда нагрузка вращается вместе с валом).

Напряжения кручения изменяются пропорционально изменению нагрузки. В большинстве случаев трудно установить действитель­ный цикл нагрузки машины в условиях эксплуатации. Тогда расчет выполняют условно по номинальной нагрузке, а циклы напряжений принимают — симметричным для напряжений изгиба (рис. 15.4, а) И отнулевым для напряжений кручения (рис. 15.4, б). Выбор от - нулевого цикла для напряжений кручения обосновывают тем, что большинство машин работает с переменным вращающим момен-

Том, а знак момента из­меняется только у ревер­сивных машин. Неточ­ность такого приближен­ного расчета компенси­руют при выборе запасов прочности.

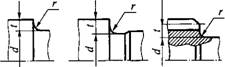
Приступая к расчету, предположительно намечают опасные се­чения вала, которые подлежат проверке (сечения I — / и II — II; Рис. 15.3). При этом учитывают характер эпюр изгибающих и вра­щающих моментов, ступенчатую форму вала и места концентрации напряжений (см. рис. 15.1). Для опасных сечений определяют запасы сопротивления усталости и сравнивают их с допускаемыми. При совместном действии напряжений кручения и изгиба запас сопроти­вления усталости определяют по формуле

S = si + S* ^ [s] « 1

Где Sa=------------------- запас сопротивления

Усталости при изгибе;

Sx=------------------ запас сопротивления уста-

KtD'Ca + Фт'Ст

Лости при кручении.

В этих формулах са и га — амплитуды переменных составля­ющих циклов напряжений, а ат и хт — постоянные составляющие.

Согласно принятому выше условию (рис. 15.4), при расчете валов

0т=О; <тв=Л//(0,Ы3); J

Tm = Ta=0,5T = 0,5r/(0,2rf3);j ( ' }

Фа и фх — коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости.

Величины фа и фх зависят от механических характеристик мате­риала.

По ГОСТ 25.504 — 82 рекомендуют

^=0,02+2-10"4 (7вЛ

] (15-6)

Гг_, и T_I — пределы выносливости. Их определяют по таблицам или приближенным формулам:

Т_,«(0,2...0,3)<гв; I (15.7)

ТВ«(0,55...0,65)<7в. J

KaD и KxD — коэффициенты концентрации напряжений в расчетном (опасном) сечении при изгибе и кручении соответственно:

(15.8)

Здесь Ке Кх — эффективные коэффициенты концентрации нап­ряжений; для ступенчатых галтельных переходов — табл. 15.1; для шпоночных пазов — табл. 15.2; для шлицевых и резьбовых участ­ков валов — табл. 15.3;

Kdn — коэффициенты, учитывающие размеры вала (масш­табный фактор); KFa, KFx — коэффициенты, учитывающие качество (шероховатость) поверхности; Kv — коэффициент, учитывающий наличие поверхностного упрочнения (табл. 15.4). При отсутствии такового Kv— 1.

Величину отношения KojKfo для валов с концентраторами напря­жений в виде канавок, галтельных переходов, поперечных отверстий и т. п. определяют по ГОСТ 25.504 — 82 или по таблицам справоч­ников. Для посадок с натягом — по эмпирической формуле: ЫКь^Кх-Кь'Къ где Кх = 0,38 +1,48Lgrf при Rf<150 мм и ^ = 3,6 при D^ 150 мм (<D — диаметр вала); К2 = 0,305 - I - 0,0014<тв (здесь и да­лее <7В в МПа); Къ = 0,65 + 0,014/7 при р^25 МПа и Къ = 1, если р> >25 МПа [р — давление посадки см. формулу (7.5)]. При кручении KclKfc « OfiKJKfo.

Величину масштабного фактора можно оценить по формуле

Где D (мм) — диаметр вала. При изгибе (К^) V=0,19—1,25 • 10~4<тв. При кручении (Кл) величину V увеличивают в 1,5 раза.

Величины коэффициентов KFa и KFx определяют по формулам: при изгибе KFa = 1 - 0,22[Lg(<тв/20)-1]LgRz, если Rz> 1 мкм, и KFa = 1 при Rz^L мкм; при кручении ^ = 0,575^+0,425. При наличии в расчетном сечении вала нескольких концентраторов напряжений в формулах (15.8) учитывают тот концентратор, у которого больше величина К* или Кх.

Таблица 15.1

Отметим, что приведенные выше табличные данные, а также эмпирические (корреляционные) формулы, позволяющие опреде­лить коэффициенты и Кт1), получены в результате обширных экспериментальных исследований [19, 22]. Их анализ показывает, что с увеличением предела прочности съ стали повышается ее чувст­вительность к резким изменениям формы, влиянию шероховатости поверхности и размеров детали. Это означает, что при разработке конструкции валов из высокопрочных сталей следует уделять осо­бое внимание уменьшению концентрации напряжений и шерохова­тости поверхности.

Сопротивление усталости можно значительно повысить, при­менив тот или иной метод поверхностного упрочнения: азотиро­вание, поверхностную закалку ТВЧ, дробеструйный наклеп, обкат­ку роликами и т. д. При этом можно получить увеличение преде­ла выносливости до 50% и более. Чувствительность деталей к по­верхностному упрочнению уменьшается с увеличением ее разме­ров.

Формулы (15.4) относятся к расчету вала на длительный срок службы.

Ограниченность срока службы и переменность режима нагрузки учитывают [при невыполнении условия (15.3)] по методике, изло­женной в гл. 8.

Проверку статической прочности производят в целях предуп­реждения пластических деформаций и разрушений с учетом крат­ковременных перегрузок (например, пусковых и т. п.). При этом определяют эквивалентное напряжение по формуле

(73K=V^ + 3?<M, (15.9)

Где

Здесь М и Т—изгибающий и вращающий моменты в опасном

Сечении при перегрузке.

322

Предельное допускаемое напряжение [<т] принимают близким к пределу текучести <гт:

[<т]«0,8<тт.

Расчет на жесткость. Упругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колес, катков фрикционных передач и т. п. От прогиба вала (рис. 15.5) в зубчатом зацеплении возникает концентрация нагрузки по длине зуба (см. рис. 8.13). При больших углах поворота в в подшип­нике может произойти защемление вала (см. правую опору на рис. 15.5). В металлорежущих станках перемещения валов (в особен­ности шпинделей) снижают точность обработки и качество поверх­ности деталей. В делительных и отсчетных механизмах упругие перемещения снижают точность измерений и т. д.

Допускаемые упругие перемещения зависят от конкретных тре­бований к конструкции и определяются в каждом отдельном случае. Введение общих норм едва ли возможно и целесообразно. Некото­рые из приближенных рекомендаций указаны ниже.

Для вала зубчатых передач стрела прогиба под колесом [у]«0,01/и — передачи цилиндрические; [у] «0,05т — конические, гипоидные, глобоидные передачи, где т — модуль зацепления.

Угол взаимного наклона валов под шестернями у <0,001 рад.

В станкостроении для валов общего назначения [у] = (0,0002...0,0003)/, где / — расстояние между опорами.

Угол поворота вала в подшипнике скольжения [0]=0,001 рад; в радиальном шарикоподшипнике [0]=0,005 рад.

Малые величины допускаемых перемещений иногда приводят к тому, что размеры вала определяет не прочность, а жесткость. В этих случаях нецелесообразно изготовлять вал из дорогих высо­копрочных сталей (если это не диктуется какими-либо другими условиями, например износостойкостью цапф).

Перемещения при изгибе в общем случае целесообразно опреде­лять, используя интеграл Мора и способ Верещагина (см. курс «Сопротивление материалов»). Для простых расчетных случаев мо­жно использовать готовые решения, приведенные в табл. 15.5. При этом вал рассматривают как имеющий постоянное сечение некото­рого приведенного диаметра.

Перемещение при кручении валов постоянного диаметра опреде­ляют по формуле

F

Q> = Tl/(GJp),

Где Q> — угол закручивания вала, рад; Т — вращающий момент; G — модуль упру­
гости при сдвиге; / — длина закручиваемого участка вала; /Р = = 7и/4/32 — полярный момент инерции поперечного сечения вала.

Таблица 15.5

Если вал ступенчатый и нагружен несколькими Г, то угол <р определяют по участкам и затем суммируют.

Величина допускаемого угла закручивания вала не однозначна. Она зависит от требований, предъявляемых к механизму. Напри­мер, в приводах следящих систем, делительных механизмах и т. д. допускаемые углы закручивания ограничивают секундами и мину­тами на 1 м длины, а в карданных валах автомобилей допускают несколько градусов на метр.

Расчет на колебания. Полагаем, что читателю известны методы расчета колебаний элементарных систем. Вынужденные колебания системы с одной степенью свободы описывают уравнением

Sin COBt,

Т (col-col)

Где у — амплитуда вынужденных колебаний массы т; F& — амп­литуда возмущающей силы I7(/)=IrasincoB/; шв — круговая частота возмущающей силы или частоты вынужденных колебаний системы; сос — круговая частота собственных колебаний системы.

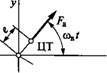
Рассмотрим уравнение (15.12) в приложении к колебаниям вала для простейшего случая (рис. 15.6). Здесь на валу, вращающемся с угловой скоростью шв, закреплен диск массой т с эксцентрисите­том е. Собственную массу вала считаем малой по сравнению с т и в расчет не принимаем (упругая система с одной степенью свободы). На вал действует центробежная сила

F^mcole,

Вектор которой вращается с угловой скоростью шв. Составляющие силы F& по осям у и z:

Fy=Fa. sin coBt, Fz=Ft cos coBt.

Силы Fy и Fz являются гармоническими возмущающими силами, которые вызывают изгибные колебания вала в направлении осей У и Z. Колебания от силы Fy описываются уравнением (15.12), а от

Силы Fz — аналогичным ему уравнением Z=———- Cos сов/.

Т(а>1-о>1)

Частота собственных изгибных колебаний

Сос=у/1/ (т5)=fgjyc.

Где S =yj(mg) — изгибная податливость вала или прогиб от еди­ничной силы; у„ — статический прогиб вала от действия силы тяжести mg диска.

Уравнение (15.12) позволяет отметить, что при соъ->сос у-*со. При сов=сос наступает резонанс.

Таким образом, даже при ничтожно малой неуравновешенности в условиях резонанса можно ожидать разрушения машины*.

Частоту вращения (мин-1), при которой наступает резонанс, называют критической:

=(30/71)0^ = (30/я)шс=(30/7T)Vg/>^. (15.16)

Если угловая скорость шв больше сожр=соС9 то система при раз­гоне перейдет зону резонанса и снова стабилизируется. Во избежа­ние поломок зону резонанса следует проходить быстро. Задержки в этой зоне не допускаются.

При соъ>сос амплитуда колебаний меняет свой знак [см. формулу (15.12)]. Установим, что практически это означает.

Полная амплитуда

Т(т1-т) co^-cot

Здесь учтено Sin2AV+Cos2A;B/=L; FK=MtnE. При соъ>сос амплитуда г направлена противоположно е и при шв»шс г->(—е). Таким образом, за критической зоной центр тяже­сти несбалансированной массы приближается к геометрической оси вращения. Это явление используют в высокоскоростных механиз­мах, когда для сохранения устойчивости устанавливают гибкий вал с низкой собственной частотой шс.

За предел вибрационной устойчивости обычно принимают для жестких валов N^OJn^, для гибких валов

При действии переменных вращающих моментов в системе воз­буждаются крутильные колебания, которые можно проанализиро­вать подобным же способом. Сведения о крутильных колебаниях для элементарных систем даны в § 17.4.

Расчетные формулы для частот собственных колебаний и крити­ческих частот вращения более сложных систем, в том числе много­массовых, см. в справочниках, а также [4].

'"Уравнение (15.12) не учитывает затухания колебаний под действием различ­ного рода сопротивлений (внутреннее трение в металле, сопротивление окружающей среды и сопряженных деталей и т. п.).

Пример расчета 15.1. Выполнить проектный расчет вала и его опор (см. рис. 15.1): 7=645 Н м, л=200 мин"1, ширина шестерни — 100 мм, диаметр шестерни d — =200 мм (г =40, т=5 мм), /?=8°; на выходном конце вала установлена упругая втулочно-пальцевая муфта; материал вала — сталь 45, улучшенная, ав=750 МПа, (7х=450 МПа. Срок службы длительный, нагрузка близка к постоянной, допускается двухкратная кратковременная перегрузка.

Решение. 1. По формуле (15.1) приближенно оцениваем средний диаметр вала при [т] = 12 МПа:

D=/(A5' 103/(0,2* 12) = 64,5 мм.

2. Разрабатываем конструкцию вала и по чертежу оцениваем его размеры: диаметр в месте посадки шестерни с натягом Dm = 65 мм; диаметр в месте посадки подшипников dn=dm—5=60 мм; диаметр в месте посадки муфты dM=dn—5 = 55 мм; /=160 мм; а=Ь=80 мм; с = 170 мм; £=140 мм.

3. Определяем допускаемую радиальную нагрузку на выходном конце вала, полагая, что редуктор может быть использован как редуктор общего назначения

FM = 250 Y/T=250 ^645=6350 Н.

4. Определяем силы в зацеплении [см. формулы (8.26)]:

Ft=2T/di =2' 645' 103/200 = 6450 Н; Fa=FttgP=6450 • Tg8°=906 Н; Fr=Fttg<x/cosp=Ft • Tg 20°/Cos 8° = 6450 • 0,364/0,9903 =2371 H.

5. Определяем реакции в опорах и строим эпюры изгибающих и вращающих моментов (см. рис. 15.3).

В вертикальной плоскости (рис. 15.3, б):

2Ж=0; Fh'l+Ma-Fta^

Где Ma=Fa d/2. Из уравнения (2) находим

F^2=(Fr'a-Fa'dl/2)/l=(23n SQ-9Q6'20Q/2)/l60=6l9 Н.

Из уравнения (1): ^=^-^=2371-619 = 1752 Н. В горизонтальной плоскости (рис. 15.3, в):

ZF=0; Fb+Fja-Fi-b

TOC o "1-3" h z ZM=0; FTR2 l-Ft a=0. (2)

Из (2) находим FTS2=Ft A/L= 6450■ 80/160 =3225 H; при этом =

= 6450-3225=3225 H [см. (1)].

В плоскости смещения валов (рис. 15.3, г):

LF=0; F^-F^-Fm-O; (1)

LM=0;F&/-/^(/+c)=0. (2)

Отсюда F%2=FM (I+с)!I = 6350 (160 +170)/160 = 13 097 Н, тогда FR =FR2~FM= 13 097-6350 = 6747 Н. Максимальные реакции в опорах (наихудший случай нагружения опор):

Fr = )2 + (FTRl )2+F%{ - у/ 7522 + 32252 + 6747 = 10 417 Н.

FM=>/(Fh)2 + (FH)2 +FB2 =V61'92 + 32252 + 13097 = 16381 Н.

6. По формулам (15.3) определяем запасы сопротивления усталости в опасных сечениях.

Просчитываем два предполагаемых опасных сечения (см. рис. 15.3, а): сечение / — / под шестерней, ослабленное шпоночным пазом, и сечение II — II ря­дом с подшипником, ослабленное галтелью. Для первого сечения изгибающий момент

MI_I=y/M2+M2+MM=y/№ll+Ma'alt)2HW№

=<У(2371 • 80' 80/160+90 600 • 80/160)2 + (6450 • 80 • 80/160)2 + + 6350-170 80/160 = 833 354 Н мм, где Ма=^/2= 906 200/2=90600 Нмм.

Вращающий момент Г=645* 103 Н мм.

Напряжение изгиба (7И=Mj _ JW* = 833 354/(0,1 • 653)=30,3 МПа. Напряжение кручения т=Г/Жр=645' 103/(0,2 '653)=11,7 МПа. По формулам (15.7),

(7_!=0,4(7В=0,4* 750=300 МПа; т_!=0,2(7в=0,2 750=150 МПа; тв=0,6(7В=0,6 • 750 = 450 МПа.

По формулам (15.8) определяем коэффициенты концентрации К^п и Kxj). В сече­нии I — I концентраторами напряжений являются: посадка шестерни на вал с натя­гом и шпоночный паз. Для посадки с натягом K<T/K(J(T=K К2Къ = 3,063 1,355 ■ 0,86 = =3,57 (см. с. 320), К{=0,38 + 1,481G</=0,38 + 1,481G65 = 3,063; К2 =0,305+0,0014(7В = =0,305+0,0014* 750 = 1,355. Полагаем, что давление посадки /7=15 МПа (расчет величины р — см. главу 7), тогда = 0,65+0,014р=0,65+0,014-15=0,86. Оцениваем величину масштабного фактора

/^=0,5^1+^ 2VJ=0,83.

Здесь V=0,19-1,25 10"4(7B=0,19-1,25 Ю"4'750=0,09625 и D=65 мм. При этом эффективный коэффициент концентрации напряжений будет равен £,=3,57 0,83 = =2,96. Для шпоночного паза, выполненного концевой фрезой (табл. 15.2), — Ка= =2,0. При расчете K^D учитываем бблыпую величину т. е. Кв=2,96.

/ 750 KFa = - 0,22 F Lg — -1J Lg 3,2=0,936,

Где шероховатость поверхности вала Rz—3,2 мкм. Kv— 1 — вал без поверхностного упрочнения.

KeD^iKa/Ktb + l/Kto - 1)/А>=(3,57 +1/0,936-1)/1 =3,638.

Далее, А^/АГЛ=0,6 -3,57=2,14; KFx=0,575KFa+0,425=0,575 0,936 + 0,425=0,963. Коэффициент концентрации напряжений в сечении / — / при кручении

Ятд=(*т/*А+ VKFx-L)/TfK=(2,14 +1/0,963-1)/1 =2,178.

По формуле (15.6) ^=0,02+2* 10"4-750=0,17; фх=0,5 0,17=0,085; =

=30,3 МПа; Ta=Tw=0,5т=0,5 ' 11,7 = 5,85 МПа [см. формулы (15.5)]. Запас сопротивления усталости при изгибе (ат—0)

Sa=300/(3,638 • 30,3)=2,72.

Запас сопротивления усталости при кручении

Sx = 150/(2,178 • 5,85 + 0,085 • 5,85) = 11,33.

При этом S=2,72 • 11,33/у/2,722 + 11,332 = 2,645 > [5] = 1,5.

Для второго сечения изгибающий момент Мя FMc=6350 • 170 = 1080' 103 Н мм; вращающий момент Т= 645 • 103 Н * мм;

(7И = 1080 • 103/(0,1' 553)=65 МПа;

Т=645 • 103/(0,2 • 553) = 19,4 МПа.

Принимаем радиус галтели г=1,25 мм и по таблице 15.1 при Tjr = (65 — 60)/ /(1,25 2)=2 и R/D= 1,25/60=0,02 находим А*«1,925 и АГХ = 1,6;

^=0,5 [1 + (60/7,5)"0'1925]=0,84;

-1.5 0.1925

К*=0,5[1+ (60/7,5) ] =0,77; (1,925/0,84+ 1/0,936-1)/1 =2,36;

*т1)=(1,6/0,77 +1/0,963-1)/1 =2,12; Sa=300/(65• 2,36) = 1,96;

Sx=150/(2,12 • 9,7+0,085 • 9,7)=7,01; S= 1,96 • 7,01/^1,962 + 7,012 =

= 1,89 >[5] = 1,5.

Больше напряжено второе сечение.

7. Проверяем статическую прочность при перегрузках — формула (15.9). При перегрузках напряжения удваиваются и для второго сечения сги = 130 МПа и т«

«39 МПа; М=0,8(7Т=0,8 450 = 360 МПа; (73I=V/L302+392 = 136<[(7]=360 МПа.

8. Проверяем жесткость вала. По условиям работы зубчатого зацепления опас­ным является прогиб вала под шестерней. Для определения прогиба используем табл. 15.2. Средний диаметр на участке / (см. рис. 15.1) принимаем равным 4п = =65 мм. Здесь

J=Ndfal64=п- 65*/64=88 10* мм4.

Прогиб в вертикальной плоскости: от силы Fr

Ув=Fra2b2L(3EJl)=2371 80^/(3 2,1 • 105 88 • 104' 160) = 0,001 мм;

От момента Ма прогиб равен нулю.

Прогиб в горизонтальной плоскости от силы Ft Ут=Iyz2B2/(3Ell)=6450 ■ 802 • 802/ /(312,1 105 88 10* • 160)=0,003 мм.

Прогиб от силы FM В плоскости смещения валов:

Ym=FMca(l2-J)/(6Eir) = =6350-170 80(1602-802)/(6 2,1 • 105 88 104-160)=0,0093 мм. Суммарный максимально возможный прогиб:

У=^у^ "T"Д'р "T"Д'м = ^0,0012 -T- 0,0032 ■+■ 0,0093 = 0,0125 мм.

Допускаемый прогиб (см. § 15.3) [у]«0,01т=0,01 5=0,05>0,0125 мм. Аналогично проверяют углы поворота в опорах (обучающимся рекомендуется самим выполнить эту проверку).

Таким образом, условия прочности и жесткости выполняются. По этим услови­ям диаметр вала можно сохранить. Однако этот вопрос нельзя окончательно решить без расчета подшипников (см. пример 16.2).