Детали машин

Практический расчет (подбор) подшипников качения

Основные критерии работоспособности и расчета. Можно отме­тить следующие основные причины потери работоспособности под­шипников качения.

Усталостное выкрашивание наблюдается у подшипников после длительного времени их работы в нормальных условиях.

Износ наблюдается при недостаточной защите от абразивных частиц (пыли и грязи). Износ является основным видом разрушения подшипников автомобильных, тракторных, горных, строительных и многих подобных машин.

Разрушение сепараторов дает значительный процент выхода из строя подшипников качения, особенно быстроходных.

Раскалывание колец и тел качения связано с ударными и виб­рационными перегрузками, неправильным монтажом, вызыва­ющим перекосы колец, заклинивание и т. п. При нормальной эксп­луатации этот вид разрушения не наблюдается.

Остаточные деформации на беговых дорожках в виде лунок и вмятин наблюдаются у тяжелонагруженных тихоходных подшип­ников.

Современный расчет подшипников качения базируют только на двух критериях:

1) Расчет на статическую грузоподъемность по остаточным деформациям;

2) Расчет на ресурс (долговечность) по усталостному выкраши­ванию. Расчеты по другим критериям не разработаны, так как эти критерии связаны с целым рядом случайных факторов, трудно поддающихся учету.

Стандартом ограничены число типов и размеров подшипников. Это позволило рассчитать и экспериментально установить грузо­подъемность (работоспособность) каждого типоразмера подшип­ников.

При проектировании машин подшипники качения не констру­ируют и не рассчитывают, а подбирают из числа стандартных по условным формулам. Методика подбора стандартных подшипни­ков также стандартизована.

Ниже излагается методика выбора подшипников, принятая оте­чественными стандартами и международной организацией по стан­дартизации ИСО (см. каталог-справочник [28]).

Различают подбор подшипников по динамической грузоподъем­ности для предупреждения усталостного разрушения (выкрашива­ние), по статической грузоподъемности для предупреждения оста­точных деформаций.

Выбор подшипников по динамической грузоподъемности С (по заданному ресурсу или долговечности) выполняют при частоте вращения л^ 10 мин" При п от 1 до 10 мин"1 в расчет принимают /2=10 мин"1.

Условие подбора:

С (потребная) (базовая). (16.26)

Базовая динамическая грузоподъемность С — это такая постоян­ная стационарная сила, которую подшипник может теоретически воспринимать в течение 1 млн оборотов без появления признаков усталости не менее чем у 90% из определенного числа подшип­ников, подвергающихся испытаниям. Величина С для каждого под­шипника приводится в каталогах, примеры см. в табл. 16.2 (для шариковых радиальных однорядных подшипников средней серии 300, ГОСТ 8338 — 75). При этом под С понимают радиальную силу Сг для радиальных и радиально-упорных подшипников (с невраща - ющимся наружным кольцом), осевую силу Са для упорных и упор - но-радиальных (при вращении одного из колец).

Динамическая грузоподъемность и ресурс связаны эмпирической зависимостью 356

Ь — аагъ (CjPf или C=Pv/L/(A,A23), (16.27)

Где L — ресурс, млн оборотов; Р — эквивалентная динамическая нагрузка (см. ниже); р—Ъ для шариковых и р—10/3«3,33 для роли­ковых подшипников; ах — коэффициент долговечности (см. ниже); агъ — обобщенный коэффициент совместного влияния качества ме­талла, особенностей технологии производства, конструкции и усло­вий эксплуатации (табл. 16.3).

Примечания: 1. Обычные условия применения. 2. Условия, характеризующиеся наличием гидродинамической пленки масла между контактирующими поверхностями колец и тел качения (Л >2,5) и пониженных перекосов в узле. 3. Когда кольца и тела качения изготовлены из сталей повышенного качества (электрошлаковой или вакуумной) и подшипники работают в условиях наличия гидродинамической пленки масла и пониженных перекосов в узле. 4. Решение задачи гидродинамической теории смазки для подшипников качения сложнее, чем для подшипников скольжения, и здесь не рассматривается. Формула для расчета параметра режима смазки Л приведена в [28].

В каталогах указаны С с коэффициентом надежности Р(/) = 0,9. В тех случаях, когда необходимо повысить надежность, величину Ах уменьшают:

Р(0 ..................................... 0,9 0,95 0,96 0,97 0,98 0,99

Ах ....................................... 1 0,62 0,53 0,44 0,33 0,21

Для подшипников большинства изделий принимают Р(/) = 0,9*.

"Повышенные P(T) допускают для подшипников повышенных классов точ­ности при высокой точности сопряженных с подшипником деталей, надежном сма­зывании и строго регламентированных режимах нагрузки и частоты вращения [28].

23-2973 3 57

При малых ресурсах ограничивают Р<0,5С, иначе возможно неусталостное разрушение.

Формула (16.27) получена в результате испытаний на усталость подшипников качения (как узла, а не материала). На основании испытаний строят кривую усталости с заданной вероятностью не­разрушения. Эта кривая подобна кривой на рис. 8.39, но отличается тем, что практически не имеет горизонтального участка, а за коор­динаты приняты: по оси абсцисс — L (млн оборотов) вместо числа циклов NK; по оси ординат — нагрузка Р вместо напряжений <тн.

Кривая аппроксимируется зависимостью PpL=Const. Константу определяют, приняв L= 1, и обозначают Ср. Тогда PpL= Ср и далее записывают в виде формулы (16.27). Величина С зависит не только от прочности материала, но также от конструктивных и технологи­ческих характеристик подшипника.

Если частота вращения п постоянна, номинальную долговеч­ность (ресурс) удобнее считать в часах:

L*=а^з (С/Р)р [10б/(60и)], или Lh=L' 10б/(60и).

Рекомендуемые Lh приведены в табл. 16.4.

Эквивалентная динамическая нагрузка Р для радиальных и ради - ально-упорных подшипников есть такая условная постоянная ста­ционарная радиальная сила Рп которая при приложении ее к подшип­нику с вращающимся внутренним кольцом и с неподвижным на­ружным обеспечивает такую же долговечность, какую подшипник имеет при действительных условиях нагружения и вращения. Для упорных и упорно-радиальных подшипников соответственно будет Ра — постоянная центральная осевая сила при вращении одного из колец:

(16.29)

Где Fn Fa — радиальная и осевая силы; X, Y — коэффициенты ради­альной и осевой сил (указываются в каталоге, см. выдержки в табл. 16.5); V — коэффициент вращения, зависящий от того, какое кольцо подшипника вращается относительно внешней нагрузки (при враще­нии внутреннего кольца V= 1, наружного V= 1,2); Къ — коэффици­ент безопасности, учитывающий характер нагрузки: спокойная КБ= 1, умеренные толчки Къ= 1,3...1,5, с сильными толчками (удара­ми) АБ=2,5...3; К? — температурный коэффициент (для стали ШХ15 при T до 100°С Кг=19 при /=125...250°С КТ= 1,05... 1,4 соответст­венно).

Таблица 16.4

Машины и оборудование

1. Приборы и аппараты, используемые периодически (демонстраци­онная аппаратура, механизмы для закрывания дверей, бытовые прибо­ры)

2. Механизмы, используемые в течение коротких периодов времени (механизм с ручным приводом, сельхозмашины, подъемные краны в сборочных цехах, легкие конвейеры)

3. Ответственные механизмы, работающие с перерывами (вспомога­тельные механизмы на силовых станциях, конвейеры поточного произ­водства, лифты, нечасто используемые металлообрабатывающие стан­ки)

4. Машины:

А) для односменной работы с неполной нагрузкой (стационарные электродвигатели, редукторы общего назначения);

Б) работающие с полной нагрузкой одну смену (машины общего машиностроения, подъемные краны, вентиляторы, распредели­тельные валы);

В) для круглосуточного использования (компрессоры, насосы, шахтные подъемники, стационарные электромашины, судовые приводы);

Г) непрерывно работающие с высокой нагрузкой (оборудование бумагоделательных фабрик, энергетические установки, шахтные насосы, оборудование торговых морских судов)

В табл. 16.S величины X и Y различны в зависимости от отношения Fa/(VFr). Объясняется это тем, что до некоторых пределов, равных коэффициенту е этого отношения, дополни­тельная осевая нагрузка не ухудшает условия работы подшипни­ка. Она уменьшает радиальный зазор в подшипнике и выравни­вает распределение нагрузки (в том числе радиальной) по телам качения.

При переменном режиме нагрузки в формулах (16.29) вместо Fr и Fa подставляют их средние величины F^ и Fma9 каждая из которых определяется по зависимости:

Fm=y?:(F?m?:Lh (1б. зо)*

Где Fi — радиальная или осевая сила соответственно, действующая на подшипник при /-том режиме нагрузки; Ls — число млн об. на /-том режиме.

♦Здесь: р=3, для более точного расчета рекомендуется р=10/3.

Для расчетов по формуле (16.30) необходимо знать циклограм­му нагружения. Расчет величин Fm упрощается, если воспользовать­ся графиками типовых режимов (см. рис. 8.42). В этом случае Fmr= =KEFr и F^=КЕ • Fm где величины Fr и Fa определяют по максималь­ной из длительно действующих нагрузок, а величину коэффициента эквивалентности КЕ — в зависимости от режима нагрузки:

Режим нагрузки........................ 0 I II Ш IV V

КЕ.................................................. 1 0,8 0,63 0,56 0,5 0,4

Проверка и подбор подшипников по статической грузоподъемно­сти. По уравнению (16.27) нагрузка Р растет с уменьшением ресурса L и теоретически не имеет ограничения. Практически нагрузка ограничена потерей статической прочности, или так называемой статической грузоподъемностью. Статическую грузоподъемность используют для подбора подшипников при малых частотах враще­ния п < 1 мин"1, когда число циклов нагружений мало и не вызывает усталостных разрушений, а также для проверки подшипников, рас­считанных по динамической грузоподъемности. Условие проверки и подбора

Р0 ^ Со»

Где Р0 — эквивалентная статическая нагрузка; С0 — статическая грузоподъемность.

Под статической грузоподъемностью понимают такую стати­ческую силу, которой соответствует общая остаточная деформа­ция тел качения и колец в наиболее нагруженной точке контакта, равная 0,0001 диаметра тела качения. При этом под С0 понимают радиальную силу для радиальных и радиально-упорных подшип­ников, осевую силу для упорных и упорно-радиальных. Величины Со указаны в каталогах для каждого типоразмера подшипника (см. табл. 16.2).

Эквивалентная статическая нагрузка

PQ=XqFf+ Y0Fa, но не меньше чем Р0=Р,, (16.31)

Где Fr и Fa — радиальная и осевая силы; Х0 и У0 — коэффициенты радиальной и осевой статических сил (см. каталог). Р0=Ра для упорных подшипников. Например:

1) AQ=0,6 и Yo=0,5 — радиальные шарикоподшипники однорядные и двухряд­ные;

2) ЛГ0=0,5 и Уо = 0,47...0,28 (при а= 12...36° соответственно) —радиально-упор - ные шарикоподшипники;

3) ^=0,5 и Lo-O^Ctga — конические и самоустанавливающиеся шарико - и роликоподшипники.

Предельная быстроходность подшипника. Ограничивается ука­занной в каталоге предельной частотой вращения Пщ>. Это наиболь­шая частота вращения, за пределами которой расчетная долговеч­ность не гарантируется. Исследованиями установлено, что интен­сивность износа и потери на трение в подшипниках качения связаны с окружной скоростью. Поэтому для оценки предельной быстроход­ности принят условный скоростной параметр (пропорциональный окружной скорости)

[Д„л]=Const,

Где Dm — диаметр окружности центров тел качения, мм; п — часто­та вращения, мин""1.

Допускаемая величина [D„Jt] зависит от конструктивных и эксп­луатационных параметров: типа подшипника, типа сепаратора, класса точности, типа смазки и др.

Например, подшипник шариковый радиальный однорядный со стальным штам­пованным сепаратором классов точности нормальный и 6 [Алл] = 5,5 * 10S при жидкой и 4,5 * 10S при пластичной смазках; шариковый упорный однорядный и при тех же параметрах [Dmn] = 1,8 ■ 105 и 1,3 • 105.

При известном [Dmn] определяют п^ для каждого типоразмера подшипника, который указан в каталогах.

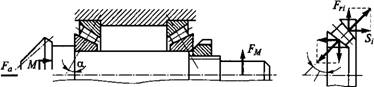
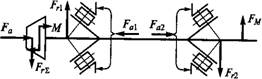
Особенности расчета нагрузки радиально-упорных подшипников связаны с наклоном контактных линий на угол а к торцовой плос­кости подшипника (см. рис. 16.13 и 16.18). На рис. 16.18 в качестве примера изображены конструктивная а и расчетная б схемы для подшипников вала конической шестерни (см. рис. 8.30). Нагрузки

В зацеплении приведены к оси вала: FrL=Y/F? + F*, M=/V41/2, где Ft, F, И Fa — по формулам (8.37) или (8.46)...(8.48)

Нагрузка на конец вала — FM.

Радиальные нагрузки подшипников Fr и Frl определяют обыч­ным способом по двум уравнениям равновесия: 0 и 2М=0. Здесь отметим только, что Fr и Frl приложены в точках пересечения контактных нормалей с осью вала. Расстояние между этими точ­ками зависит от схемы расположения подшипников и величины угла а. Если каждый подшипник на рис. 16.18 развернуть в плоско­сти чертежа на 180° с соответствующим изменением положения упорных буртиков, то точки приложения сил Fri и Frl сместятся внутрь, расстояние между ними (как плечо действия сил) уменьшит­ся, а силы Fri и FT2 возрастут — неблагоприятный вариант.

Для определения двух осевых нагрузок FaX и F& имеем только одно уравнение 0, или

Fa-Fai+Fa2 = 0,

Где за ось х принята ось вала.

В общем случае Fai не равна F&, поэтому для решения нужны дополнительные условия. Рассмотрим эти условия. Наклон кон­тактных линий в радиально-упорных подшипниках приводит к то-

Му, что радиальные нагрузки Fr сопровождаются внутренними осе­выми силами S, которые стремятся раздвинуть кольца подшипника в осевом направлении (рис. 16.18, в). Этому препятствуют упорные буртики вала и корпуса с соответствующими реакциями Fa и Fa2. Очевидно, должно быть

Fal^Sx [33]Fa2^S2, (16.33)

Иначе кольца раздвинутся (расчет сил S см. ниже).

Кроме того, для решения задачи принимают*, что в одном из подшипников осевая сила равна минимально возможной по усло­вию нераздвигания колец, т. е. Приняв, например Fa—Su получим

Fa = S—Fa9 (16.34)

И если при этом Fa2^S2, то осевые силы определены правильно. Если Fa2<S2, то принимают Fd2 — S2 И находят

Fal=S2 + Fa. (16.35)

При этом обязательно выполняется условие FaX^Su так как при Fa = S было Fa2<S2, а при увеличении F& должна увеличиваться и FaX [см. уравнение (16.32)].

Величины сил S зависят от типа подшипника, угла а и условий сборки или регулировки подшипников. Если подшипники собраны с большим зазором, то всю нагрузку воспринимают только один или два ролика. При этом (рис. 16.18, в) S^I^Tga, где i — в общем случае номер опоры.

Большие зазоры приводят к быстрому разрушению подшип­ников и поэтому недопустимы. Обычно устанавливают зазоры, близкие к нулю. В этом случае под нагрузкой находится примерно половина тел качения, а суммарная осевая составляющая

S^E'F» (16.36)

Где е' — коэффициент минимальной осевой силы.

Для радиально-упорных шарикоподшипников с номинальным углом контакта а<18° величина е' является функцией отношения (К/С0)* (см. [15,22]). При а^18° е'-е. Для конических роликопод­шипников е' = 0,83 е, где е — параметр осевой нагрузки (см. табл. 16.5).

Пример 16.2. Подобрать подшипники для вала редуктора (см. рис. 15.1), исполь­зуя данные примера 15.1: диаметр в месте посадки подшипников D= 60 мм, п — =200 мин"1, ресурс 20000 ч, режим нагрузки II — по рис. 8.42 и табл. 16.4, допускаются двукратные кратковременные перегрузки, температура подшипника /<100°С, реакции опор по рис. 15.3: /^ = 10417 Н, /^ = 16381 Н, Fa=906 Н и на­правлена в сторону левой опоры.

Решение. Учитывая сравнительно небольшую осевую силу Fa, предваритель­но назначаем шариковые радиальные подшипники средней узкой серии, условное обозначение 312, для которых по каталогу С=81900 Н, Со=48 000 Н, Лщ,= = 6000 мин"1. Определяем эквивалентную динамическую нагрузку на подшипник по формуле (16.29) с учетом переменного режима нагружения, предварительно опреде­лив: Fmri =0,63 10417 = 6562,7 Н; Fmal=0,63 906 = 570,8 Н; /W2=0,63• 16381 = = 10320 Н. Здесь КЕ=0,63 — см. табл. на с. 360. /^Fll/C0 = 570,8/48000 = 0,012. Отметим, что в случаях получения величин этого отношения, отличающихся от приведенных в табл. 16.5, поиск У и е осуществляют линейной интерполяцией или по формулам, приведенным в [22]. В нашем случае для назначенных подшипников

Е=0,528 (FJCo)0'24=0,528 (570,8/48ООО)0,24=0,182, где F^F^I-

При V— [см. примечания к формуле (16.29)] F^I/IVF^) = 570,8/6562,7 = —0,087<е. При этом Х= 1: У=0. По рекомендациям к формуле (16.29) принимаем КБ — 1 3 К 1

По формуле (16.29): РгХ = 6562,7 • 1,3 = 8531,5 Н; Ргг= 10 320 • 1,3 = 13 416 Н. Так как Pf2 > Pfi, то подбор подшипников проводим для правой опоры, как более нагруженной.

Согласно (16.27), определяем потребную динамическую грузоподъемность подшип­ника, приняв £11 = 1 и £123 = 1 (см. табл. 16.3): С=13 416^240=83 373 Н, где L=60NLfJ6 = 60 200 -20000/106 = 240 млн об.

Получен результат, когда потребная динамическая грузоподъемность превышает базовую (С=81 900 Н) на 1,8%, следовательно, расчетный ресурс подшипника 312 будет меньше заданного и составит [см. (16.27) и (16.28)] ■ A2I(CIPf • 10б/60 =

= 1 • 1 (81900/1341 б)3'10б/(60-200) = 18958 ч (отклонение от заданного ресурса — 5,2%).

Отметим, что величина расчетного ресурса (при а = 1) является минимальной или гарантированной для 90% подшипников определенной партии. Фактический же ресурс подшипников существенно больше расчетного. Проверим выполнение усло­вия Рщах^О^ С (см. с. 358). Находим параметр осевой нагрузки для подшипника левой опоры е=0,528(/7а1/С0)0'24 =0,528 (906/48000)0'24=0,2. При этом Fal/(VFrl) = =906/(1 • 10417)=0,087<е. По формуле (16.29), принимая X=L, A Y= 0, определяем максимальную эквивалентную динамическую нагрузку, действующую на подшип­ник в левой опоре. PrM&3L = VFrlKBKr = L-10417-1,3-1=13542,1 Н. В правой опоре Fa2=0, поэтому Рг2тлх = VF^K^^L' 16381 -1,3-1 =21295,3 Н. Получили, что •^>гтах=^>г2тах<^0,5С=0,5 - 81900 =40950 Н. Требуемое условие выполняется. С уче­том двукратной перегрузки проверим подшипник 312 по статической грузоподъем­ности. По формуле (16.31): для левой опоры — Р0 = 2(0,6* 10417+0,5 906) = 13406 Н < Со; для правой опоры: Ро=2 * 16 381 = 32 762 Н < С0. Условие Р0 < С0 выполняется.

Учитывая изложенное выше, а также то обстоятельство, что опорные реакции определялись как максимально возможные (наихудший случай) [см. пример расчета 15.1], следует признать подшипник 312 удовлетворяющим исходным данным приме­ра 16.2 [см. также поз. 4д и б табл. 16.4].

Пример 16.3. Подобрать подшипники для вала конической шестерни, нагружен­ного по рис. 16.18: /1=960 мин-1, срок службы L^—10000 ч, режим нагрузки I (по рис. 8.42 и по позиции 3, табл. 16.4), допускается двукратная перегрузка, температура подшипника F<100°C. Полагаем, что из предыдущего расчета вала известно: Fr = =2100 Н, />2 = 645 Н, Fa= — 1064 Н, диаметр вала </=30 мм.

Решение. Предварительно назначаем конические подшипники легкой серии, усло­вное обозначение 7206, для которых по справочнику [26] находим: а=14°; С0=22000 Н; яЩ)=8500 мин"1 при жидком смазочным материале; в=0,36; при FJ(VFr)>E У= 1,65.

Выполняем проверочный расчет. По формуле (16.36), где е'=0,83^=0,83 -0,36 = =0,3, находим минимальные осевые силы в опорах: 5J=0,3 -2100 = 630 Н; £2=0,3-645 = 193,5 Н. Принимаем Fal =SX= 630 Н и по формуле (16.34) определяем Fa2 = 630—(—1064) = 1694 Н>£2 = 193,5 Н.

Условия (16.33) удовлетворяются. Следовательно, осевые силы, действующие на подшипники, найдены правильно.

Максимальная эквивалентная динамическая нагрузка — по формуле (16.29) при V= 1; КТ=1; КБ = 1,3: левая опора — FJ(VFrl)=630/(1 -2100)=0,3<е=0,36. Соглас­но табл. 16.5 ЛГ= 1; У=0 и Prlmax= VFrXK^ = -2100* 1,3■ 1 =2730 Н; правая опо­ра — Fa2/(VFr2)= 1694/(1 • 645)=2,63 >е=0,36, поэтому по табл. 16.5 или справочнику определяем ЛГ=0,4; 7= 1,65. Pr2Max=(XVFr2 + YFa*)KBKT=(0,4 • 1 ■ 645 +1,65 • 1964)1,3 • 1 = =4548,2 Н. Так как Pr2 тах > Рг тах, то подбор подшипников выполняем по правой опоре, как более нагруженной.

Для режима I переменной нагрузки эквивалентная динамическая нагрузка в пра­вой опоре может быть определена как Pr2=KEPj2MBX=0Fi -4548,2=3638,6 Н, где KE=0Fi — см. с. 360.

Отметим, что расчет средних величин нагрузок при переменном режиме нагруже­ния и дальнейшем определении Рг2 по формуле (16.29) даст тот же результат, который получен нами выше. Это связано с тем, что параметр осевой нагрузки конических подшипников не зависит от величины осевой силы.

Потребная динамическая грузоподъемность: по формуле (16.27) при аг = 1 (с. 357); а23=0,7 (табл. 16.3) и заданном ресурсе L=60NLfJ6 = 60 '960' 10000/10б = = 576 млн-об.

С=3638,6 576/(1 *0,7) =27265,8 Н<С=31000 Н. Проверим выполнение усло­вия Ртах <0,5С (СМ. С. 358): Ргтах = Л-2тах=4548>2 Н <0,5 • 31000= 15500 Н. Условие выполняется.

Проверим этот подшипник по статической грузоподъемности с учетом действия кратковременной двукратной перегрузки. По формуле (16.31) при ЛГ0=0,5 и У0 = =0,91 — см. [26], или приближенно 70=0,22Ctgl4°«0,9 — см. с. 361, Р02 = =2(0,5-645+0,91 • 1694)=3728,1 Н<С0=22000 Н.

Условие (с. 361) выполняется. Вывод: подшипник 7206 удовлетворяет исходным данным примера.