Детали машин

Основы расчета ременных передач

Теоретические основы расчета являются общими для всех типов ремней.

Критерии работоспособности и расчета. Основными критериями работоспособности ременных передач являются: тяговая способ­ность, определяемая силой трения между ремнем и шкивом, долго­вечность ремня, которая в условиях нормальной эксплуатации огра­ничивается разрушением ремня от усталости.

В настоящее время основным расчетом ременных передач явля­ется расчет по тяговой способности. Долговечность ремня учи­тывают при расчете путем выбора основных параметров пере­дачи в соответствии с рекомендациями, выработанными практи­кой.

Кинематические параметры. Окружные скорости на шкивах

Vx = 7и/1л1/60; V2=Nd2N2L60. (12.1)

Учитывая упругое скольжение ремня, можно записать V2<Vx или

I*=*I(L - в), (12.2)

Где е — коэффициент скольжения*. При этом передаточное от­ношение

I=Nxln2=Vxd2L(V2Dx)=D2L[Dx (1-е)]. (12.3)

В дальнейшем показано, что величина е зависит от нагрузки, поэтому в ременной передаче передаточное отношение не является строго постоянным. При нормальных рабочих нагрузках « 0,01...0,02. Небольшая величина е позволяет приближенно прини­мать

(12.4)

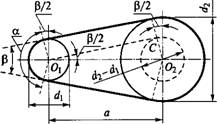
Геометрические параметры передачи. На рис. 12.2, а — межосе­вое расстояние; /? — угол между ветвями ремня; а — угол обхвата ремнем малого шкива. При геометрическом расчете известными обычно являются Du D2 и а, определяют угол а и длину ремня /. Вследствие вытяжки и провисания ремня а и / определяются при­ближенно:

А=180°—/?; Sin (Ji/2)=(D2 — Dx)/(2A).

Учитывая, что /?/2 практически не превышает 15°, приближенно принимаем sin(/?/2)=/?/2 и запишем

♦Причина скольжения рассматривается ниже.

/f« (fi?2 — dx)/а (рад) « «57(й?2-й?,)/а°. При этом

А = 180° — 57 —di)/a,

Или

А = 180° — 57rfi (i — 1)/а.

(12.5)

Длина ремня определяется как сумма прямолинейных участков и дуг обхвата:

/« 2 а+0,5я (d2+dx)+(d2 - rf,)2/(4e). При заданной длине ремня межосевое расстояние

21-П (d2+di)+у/121-11 (d1+d1)]2-S (d2-d{)2

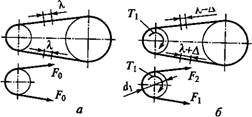
Силы и силовые зависимости. На рис. 12.3 показано нагружение ветвей ремня в двух случаях: ^ = 0 (рис. 12.3, а) и Т{>0 (рис. 12.3, Б). Здесь обозначено: F0 — сила предварительного натяжения рем­ня; Fi и F2 — силы натяжения ведущей и ведомой ветвей в нагружен­ной передаче; Ft—2Txdx — окружная сила передачи.

По условию равновесия шкива имеем

Т = 0,5Rfi (F — F2),

Или

F F2—Ff.

Связь между F0, Fx и F2 можно установить на основе следующих рассуждений.

Геометрическая длина ремня не зависит от нагрузки [см. фор­мулу (12.6)] и остается неизменной как в ненагруженной, так и в на­груженной передаче. Следовательно, дополнительная вытяжка веду­щей ветви компенсируется равным сокращением ведомой ветви (рис. 12.3). Запишем

Fi =F0+AF, F2=F0-AF, F^F2=2F0.

Из равенств (12.8) и (12.9) следует:

Fx=Fo+Ft/29 F2=FQ-Ft/2. (12.10)

Получили систему двух уравнений с тремя неиз­вестными: F0, FX9 F2. Эти Уравнения устанавливают изменение натяжений ве­дущей и ведомой ветвей в зависимости от нагрузки Ft9 но не вскрывают способности передавать эту нагрузку или тяговой спосо­бности передачи, которая связана с величиной силы трения между ремнем й шкивом. Такая связь установлена Эйлером.

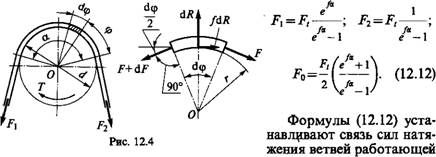
На рис. 12.4 F— сила натяжения ремня в сечении под углом Q>; CLR — нормальная реакция шкива на элемент ремня, ограниченный углом Dq>;FdR — элементарная сила трения. По условиям равнове­сия,

RF+RfdR—R(F+DF) = 0 (сумма моментов)

Или FdR=DF;

DR -F Sin (Dq>/2) - (F+ DF) Sin (Dq>/2) = 0 (сумма проекций).

Отбрасывая члены второго порядка малости и принимая sin (d<j0/2)«d<p/2, получаем

DR=Fd<P.

Исключая dR, находим

Интегрируя, получаем

Л «

Fd F [ fA t Fx Fx *

J "jF = J 1П7Г/а; H*' '

Или

Fx=F2Ef*.

Решая совместно уравнения (12.8) и (12.11) с учетом (12.9), находим:

Передачи с нагрузкой Ft и факторами трения/и а. Они позволяют также определить минима­льно необходимую силу предварительного натяжения ремня F0, при которой еще возможна передача заданной нагрузки Ft.

Если

То начнется буксование ремня[26].

Нетрудно установить [см. формулу (12.12)], что увеличение / и а благоприятно отражается на работе передачи. Эти выводы приняты за основу при создании конструкций клиноременной пе­редачи и передачи с натяжным роликом (см. рис. 12.17 и 12.16). В первой передаче использован принцип искусственного повыше­ния трения путем заклинивания ремня в канавках шкива. Во вто­рой — увеличивают угол обхвата а установкой натяжного ро­лика.

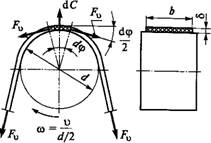
При круговом движении ремня со скоростью v (рис. 12.5) на каждый его элемент с массой dm, расположенный в пределах угла обхвата, действуют элементарные центробежные силы dС. Действие этих сил вызывает дополнительное натяжение Fv во всех сечениях ремня. Элементарная центробежная сила

D С=(Dm)V2/(095D)=р (D<P095DA)V2/(095D)=PAv2Dq>9

Где р—плотность материала ремня; A = bS — площадь попереч­ного сечения ремня. Из условия равновесия элемента ремня на­ходим

D С=2FV Sin (Dq>/2)« Fvdq>.

Подставляя, находим

Fv=pAv2. (12.13)

Натяжение Fv ослабляет полезное действие силы пред­варительного натяжения F0. Оно уменьшает силу трения и тем самым понижает на­грузочную способность пе­редачи.

Как показывают расчеты (см. ниже), влияние центро­бежных сил на работоспособность передачи существенно только при больших скоростях: г; >20 м/с.

Напряжения в ремне. Наибольшие напряжения создаются в веду­щей ветви ремня. Они складываются из ои GV И <ти:

0I=FI/A9 Av=FJA = Pv2. (12.14)

Учитывая формулу (12.10), напряжение <гг можно представить в виде

Сх =F0/A + 0,5 FJA = <70+0,5 о* (12.15)

Где

At=FJA (12.16)

— так называемое полезное напряжение; <х0 — напряжение от пред­варительного натяжения. Согласно формуле (12.8), полезное напря­жение можно представить как разность напряжений ведущей и ве­домой ветвей: ot=ox —о2.

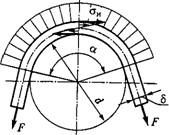
В той части ремня, которая огибает шкив, возникают напряже­ния изгиба аи (рис. 12.6). По закону Гука,

Где е — относительное удлинение, Е — модуль упругости. Вели­чину 8 найдем, рассматривая участок дуги ремня, ограниченный углом dq>. Длина нейтральной (средней) линии на этом участке равна (rf/2+<5/2)d<jc>, а длина наружней линии (rf/2 + <5)d<p. Удлинение наружного волокна будет (rf/2 + <5)d<p — (rf/2+<5/2)d<p=(<5/2)d<jc>. Отно­сительное удлинение e = (S/2)d(p/[(d/2+S/2)d(p]=5/(d + 5). Величиной 8 в знаменателе можно пренебречь как малой по сравнению с d. При этом 8=S/d9 а

AK=E6/d. (12.17)

Формула (12.17) позволяет отме­тить, что основным фактором, опреде­ляющим величину напряжений изгиба, является отношение толщины ремня к диаметру шкива. Чем меньше это отношение, тем меньше напряжение изгиба в ремне.

Суммарное максимальное напряже­ние в ведущей ветви в месте набегания ремня на малый шкив

Ffmax=0'l + 0* + Ои =

= (Т0 + 0,5(7, + <TV + <7И. (12.18)

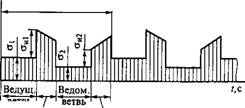
Эпюра распределения напряжений по длине ремня изображена на рис. 12.7.

Влияние отдельных составляющих суммарного напряжения на тя­говую способность передачи и долговечность ремня. Тяговая способ­ность передачи характеризуется величиной максимально допусти­мой окружной силы Ft или полезного напряжения Ot.

Учитывая формулу (12.12), нетрудно убедиться, что по условию отсутствия буксования допустимая величина ot возрастает с увели­чением напряжения <т0 от предварительного натяжения

Ot=2cq —-- . (12.19)

Однако практика показывает значительное снижение долговеч­ности ремня с увеличением <т0. Так, например, для клиновых ремней [11,30]:

(Т0, МПа ................................................................. 0,9 1 1,2 1,5 1,8

Относительная долговечность, % .................... 420 250 100 33 13

Поэтому рекомендуют принимать:

Для клиновых ремней........................... <х0^1,5 МПа

Для плоских ремней.............................. а0 < 1,8 МПа

Величина полезного напряжения ot (величина нагрузки) влияет на долговечность примерно так же, как и <т0. При указанных вели­чинах (т0 допустимое напряжение at не превышает 2,0...2,5 МПа.

Оценивая напряжения от центробежных сил по формуле (12.14), приближенно примем р«1000 кг/м3 (для хлопчатобумажных, шер - 274

Рис. 12.7

Стяных и кожаных ремней 1000 кг/м3, для прорезиненных и кли­новых 1100...1250 кг/м3). Тогда

При 17=10 м/с (гв=0,1 МПа; » V=20 м/с Av=0,4 МПа;

» 17=40 м/с Uv = 1,6 МПа.

Таким образом, для наиболее распространенных на практике среднескоростных (v<20 м/с) и тихоходных (v<10 м/с) ремен­ных передач влияние напряжений от центробежных сил несущест­венно.

Оценивая напряжения от изгиба ремня по формуле (12.17), при­мем £=200 МПа (Е для различных материалов ремней колеблется в пределах 100...350 МПа). Тогда

При djd = 200 6ГИ = 1 МПа;

<//<5=100 бги = 2 МПа;

D/5 = 50 TrH=4 МПа; Dlд = 25

Сопоставляя величины различных составляющих суммарного напряжения в ремне и учитывая, что по соображениям компакт­ности в передачах стремятся принимать небольшим отношение D/8, Можно отметить напряжения изгиба как наибольшие. Часто эти напряжения в несколько раз превышают все другие составляющие суммарного напряжения в ремне.

В отличие от а0 и Ct увеличение сги не способствует повышению тяговой способности передачи. Более того, напряжения изгиба, как периодически изменяющиеся, являются главной причиной усталост­ного разрушения ремней.

Для иллюстрации влияния напряжений изгиба на долговечность ниже приведены результаты испытаний клинового ремня [типа С(В)] при различных диаметрах шкива [11, 30]:

D, мм....................................................... 160 180 200 225 250 280

Относительная долговечность, % ...... 30 56 100 200 375 600

Поэтому на практике величину <хи ограничивают минимально допускаемыми отношениями db [см. формулу (12.25)].

Долговечность ремня зависит не только от величин напряжений, но также от характера и частоты цикла изменения этих напряжений (рис. 12.8). Частота цикла напряжений равна частоте пробегов ремня:

£/=*//, (12.20)

Где V — окружная скорость; / — длина ремня.

Чем больше С/, тем меньше долговечность ремня. Поэтому введены ограничения на частоту пробегов ремня:

Для плоских ремней 3...5 с"1, » клиновых » £/<10...20 с-1.

Предельные рекомендуемые величины U косвенно ограничивают минимальную длину ремня [см. формулу (12.20)] или межосевое расстояние [см. формулу (12.7)]. Рекомендации по выбору меж­осевых расстояний приведены в формуле (12.25).

Снижение долговечности при увеличении частоты пробегов свя­зано не только с усталостью, но и с термостойкостью ремня. В результате гистерезисных потерь при деформации ремень нагре­вается тем больше, чем больше частота пробегов. Перегрев ремня приводит к снижению прочности.

Один пробег Практика эксплуатации

Позволила установить, что при соблюдении указанных рекомендаций по выбору основных параметров пе­редачи средняя долговеч­ность. ремней составляет 2000...3000 ч.

Скольжение в передаче. Исследования Н. Е. Жуковс­
кого показали, что в ременных передачах следует различать два вида скольжения ремня по шкиву: упругое скольжение и буксование. Упругое скольжение наблюдается при любой нагрузке передачи, а буксование — только при перегрузке.

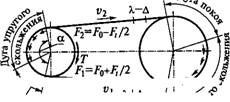
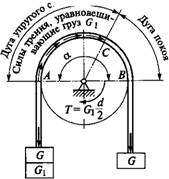
Природа упругого скольжения может быть установлена из опи­санного ниже опыта. На рис. 12.9 изображен ремень на заторможен­ном шкиве (момент торможения Т). В начале опыта к концам ремня подвешивают равные грузы G. Под действием этих грузов между шкивом и ремнем возникают некоторое давление и соответству­ющие ему силы трения. В этом состоянии левую ветвь ремня нагружают добавочным грузом G. Если груз больше сил трения между ремнем и шкивом, то равновесие нарушится и ремень со­скользнет со шкива. В противном случае состояние равновесия сохранится. Однако при любом малом грузе Gx левая ветвь ремня получит некоторое дополнительное удлинение. Величина относи­тельного удлинения, постоянная для свободной ветви ремня, будет постепенно уменьшаться на дуге обхвата и станет равной нулю в некоторой точке С. Положение точки С определяется по условию равенства груза Gx и суммарной силы трения, приложенной к ремню на дуге АС. Дополнительное упругое удлинение ремня сопровожда­ется его скольжением по шкиву. Это скольжение принято называть упругим скольжением, а дугу АС — дугой упругого скольжения. На дуге ВС ремень останется в покое. Эту дугу называют дугой покоя. Сумма дуг упругого скольжения и покоя равна дуге обхвата, опре­деляемой углом а. Чем больше (?ь тем больше дуга упругого скольжения и меньше дуга покоя. При возрастании Gx до величины, равной запасу сил трения, дуга покоя станет равной нулю, а дута упругого скольжения распространится на весь угол обхвата — рав­новесие нарушится (буксование).

По аналогии с этим в работающей ременной передаче роль грузов G выполняет сила натяжения ве­домой ветви F2, а роль дополнительного груза G — окружная сила Ft. Разность натяжения ведомой и ведущей ветвей, создаваемая нагрузкой, вызывает упру­гое скольжение в ременной передаче. При этом дуги упругого скольжения располагаются со стороны сбегающей ветви (рис. 12.10) (здесь нагрузка ведо­мого шкива аналогична показанной на рис. 12.9).

Отметим некоторый участок ремня длиной X в ненагруженной передаче и затем дадим нагрузку (рис. 12.10). При прохождении ведущей ветви отмечен- Рис. 12.9

Ныи участок удлинится до Л+А, а на ведомой сокра­тится до Л—А. Определяя окружные скорости шкивов по совместному перемеще­нию с ремнем на участках дуг покоя, получаем:

Для ведущего шкива v{ =

Для ведомого шкива V2 =

= (Я-А)//,

Или

V2<Vu

Где T — время набегания отмеченного участка ремня на шкивы. Разность скоростей V{ и V2 учитывается в формулах (12.2) и (12.3) коэффициентом скольжения г. По мере увеличения нагрузки (увели­чивается А) разность окружных скоростей возрастает, а передаточ­ное отношение изменяется. Упругое скольжение является причиной некоторого непостоянства передаточного отношения в ременных передачах и увеличивает потери на трение.

Потери в передаче и КПД. Потери мощности в ременной пере­даче складываются из потерь в опорах валов; потерь от скольжения ремня по шкивам; потерь на внутреннее трение в ремне, связанное с периодическим изменением деформаций, и в основном с дефор­мациями изгиба (см. рис. 12.8); потерь от сопротивления воздуха движению ремня и шкивов.

Все эти потери трудно оценить расчетом, а поэтому КПД пере­дачи определяют экспериментально.

При нагрузках, близких к расчетным, средний КПД для плоскоременных передач г}я0,97, для клиноременных 0,96.

Кривые скольжения и КПД. Работоспособность ременной пере­дачи принято характеризовать кривыми скольжения и КПД (рис. 12.11). Такие кривые являются результатом испытаний ремней раз­личных типов и материалов. На графике по оси ординат отсчитыва­ют относительное скольжение е и КПД, а по оси абсцисс — нагруз­ку передачи, которую выражают через коэффициент тяги

Ф = Ftj (2Fq)=Atl (2ао).

Коэффициент тяги Q> позволяет судить о том, какая часть предварительного натяжения ремня F0 используется полезно для передачи нагрузки Fh т. е. характеризует степень загруженности передачи. Целесообразность выражения нагрузки передачи через

Безразмерный коэффициент Q> Объясняется тем, что скольже­ние и КПД связаны именно е, % со степенью загруженности пе- редачи, а не с абсолютной ве­личиной нагрузки. 3

На начальном участке кри­вой скольжения от 0 до щ наб - 2 людается только упругое ско­льжение. Так как упругие де - 1 формации ремня приближенно подчиняются закону Гука, этот о участок близок к прямолиней­ному. Дальнейшее увеличение нагрузки приводит к частично-

Упругое скольжение, так и буксование. Долю каждого из них на графике можно оценить продолжением прямой г штриховой лини­ей. Величину срО принято называть критическим коэффициентом тяги.

Рабочую нагрузку рекомендуют выбирать вблизи Q>0 и слева от него. При этом передача будет иметь максимальный КПД. Работу в зоне частичного буксования допускают только при кратковремен­ных перегрузках, например при пуске. В этой зоне КПД резко снижается вследствие увеличения потерь на скольжение ремня, а ре­мень быстро изнашивается. Размер зоны частичного буксования характеризует способность передачи воспринимать кратковремен­ные перегрузки.

Отношение фшах/фо для ремней: плоских кожаных и шерстя­ных — 1,35...1,5; прорезиненных — 1,15...1,3; хлопчатобумажных — 1,25... 1,4; клиновых — 1,5... 1,6.

Допускаемые полезные напряжения в ремне. Определив по кри­вым скольжения щ, находят полезное допускаемое напряжение для испытуемой передачи (см. предыдущую формулу):

[Ajo=2<Po0"O/'Y,

Где 1,2...1,4 — запас тяговой способности по буксованию.

Кривые скольжения получают при испытаниях ремней на типо­вых стендах при типовых условиях: а =180°, V= м/с, нагрузка равномерная, передача горизонтальная. Данные заносят в таблицы. Допускаемые полезные напряжения [crj0 (МПа) в плоских ремнях при <т0 =1,8 МПа приведены в табл. 12.1.

Переход от [(г,]0 для типовой передачи к допускаемым полезным напряжениям [а] для проектируемой передачи производят с по­мощью корректирующих коэффициентов:

[о J = [crJoCaCvCpCo,

Где Ca — коэффициент угла обхвата, учитывающий снижение тяго­вой способности передачи с уменьшением угла обхвата:

А, град......... 150 160 170 180 200 220

Са................ 0,91 0,94 0,97 1,0 1,1 1,2

Cv — скоростной коэффициент, вводимый только для передачи без автоматического регулирования натяжения (см. ниже) и учитыва­ющий уменьшение прижатия ремня к шкиву под действием центро­бежных сил:

17, м/с......... 5 10 15 20 25 30

Cv ................ 1,03 1,00 0,95 0,88 0,79 0,68

Ср — коэффициент режима нагрузки, учитывающий влияние пери­одических колебаний нагрузки на долговечность ремня.

Нагрузка Спокойная Умеренные Значительные Ударная и резко

Колебания колебания переменная

Ср 1...0,85 0,9...0,8 0,8...0,7 0,7...0,6

Примечание. Меньшая величина — для поршневых и других подобных двигателей.

С0 — коэффициент, учитывающий способ натяжения ремня и на­клон линии центров передачи к горизонту (у вертикальных пере­дач собственная масса ремня уменьшает его прижатие к нижнему шкиву):

Угол наклона линии центров передачи к горизовггу 0...600 60...800 80...900 Передачи с автоматическим натяжением Со 111

Передачи с периодическим подтягиванием Со 1 0,9 0,8

Формула (12.23) является общей для всех типов ременных пере­дач. На практике в таком виде ее используют только при расчете

280
Плоскоременных передач. Особенности расчета клиноременных пе­редач рассматриваются ниже (см. § 12.4).

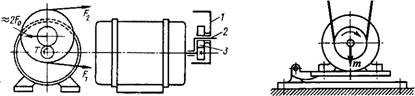
Способы натяжения ремней. Выше показано, что величина си­лы JF0 натяжения ремня оказывает существенное влияние на дол­говечность, тяговую способность и КПД передачи. Наиболее эко­номичными и долговечными являются передачи с малым запасом трения (с малым запасом JF0). На практике большинство передач работает с переменным режимом нагрузки, а расчет передачи вы­полняют по максимальной из возможных нагрузок. При этом в пе­редачах с постоянным предварительным натяжением F0 в перио­ды недогрузок излишнее натяжение снижает долговечность и КПД. С этих позиций целесообразна конструкция передачи, у кото­рой натяжение ремня автоматически изменяется с изменением на­грузки, т. е. отношение Ft/FQ=Const. Пример такой передачи пока­зан на рис. 12.12. Здесь ременная передача сочетается с зубча­той. Шкив 1 установлен на качающемся рычаге 2, который явля­ется одновременно осью ведомого колеса 3 зубчатой передачи. Натяжение 2JF0 ремня равно окружной силе в зацеплении зубча­той передачи, т. е. пропорционально моменту нагрузки. Преиму­ществом такой передачи является также то, что центробежные силы не влияют на тяговую способность (передача может рабо­тать при больших скоростях). Недостатки передачи — слож­ность конструкции и потеря свойств самопредохранения от пере­грузки.

На рис. 12.13 показан пример схемы передачи, в которой натяжение ремня автоматически поддерживается постоянным. Здесь натяжение осуществляется массой т электродвигателя, установ­ленного на качающейся плите. Постоянное натяжение получают также в передачах с натяжным роликом (см. рис. 12.16, е).

Третьим способом натяжения является способ периодическо­го подтягивания ремня (по мере его вытяжки) с помощью винта или другого подобного устройства (рис. 12.14), где двигатель мож­но перемещать по салазкам плиты. Периодическое регулирование натяжения требует систематического наблюдения за передачей и в случае недосмотра приводит к буксованию и быстрому износу ремня.

Рис. 12.15

Нагрузка на валы и опоры. Силы натяжения ветвей ремня (за исключением Fv) передаются на валы и опоры (рис. 12.15). Равно­действующая нагрузка на вал

Fr=Y/Fl+Fi+2FtF2CosP к 2F0 cos (0/2). (12.24)

Обычно Fr в 2...3 раза больше окружной силы Ft (см. пример расчета), и это, как указывалось выше, относится к недостаткам ременной передачи (в зубчатой передаче Fr&Ft).