Детали машин

Муфты упругие

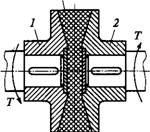
Назначение и динамические свойства муфт. Конструкция одной из упругих муфт изображена на рис. 17.8. Эту конструкцию можно рассматривать как принципиальную схему, общую для всех упругих муфт. Здесь полумуфты 1 и 2 связаны упругим элементом 3 (напри­мер, склеены или привулканизированы). Упругая связь полумуфт позволяет: компенсировать несоосность валов; изменить жесткость системы в целях устранения резонансных колебаний при периоди­чески изменяющейся нагрузке; снизить ударные перегрузки.

Одной из основных характеристик упругой муфты является ее жесткость:

C^DT/Dq), (17.9)

Где Т — вращающий момент, передаваемый муфтой; ср — угол за­кручивания муфты моментом Г. В зависимости от характеристики С9 (рис. 17.9) различают упругие муфты постоянной 1 и переменной 2 жесткости. Для муфт постоянной жесткости

Сф=7Уф=Const.

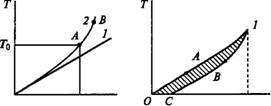
Переменной жесткостью обладают муфты с неметаллическими упругими элементами, материалы которых (резина, кожа и т. д.) не подчиняются закону Гука, а также муфты с металлическими упругими элементами, условия деформирования которых задают­ся конструкцией. От характеристики жесткости упругой муфты в значительной степени зависит способность машины переносить резкие изменения нагрузки (удары) и работать без резонанса ко­лебаний. Например, допустим, что работа в точке А муфты с пе­ременной жесткостью (рис. 17.9) соответствует условиям резонан­са. При этом возрастает амплитуда колебаний, а максимальные величины Т и ср соответствуют точке В. Но в точке В муфта име­ет другую жесткость, при которой резонанса нет. Система будет возвращаться к точке А и т. д. Следовательно, при муфте с перемен­ной жесткостью не может быть резонанса в полном смысле этого понятия.

Важным свойством упругой муфты является ее демпфирую­щая способность, которая характеризуется энергией, необратимо поглощаемой муфтой за один цикл (рис. 17.10): нагрузка (ОА1) И разгрузка (1ВС). Как известно, эта энергия измеряется площа­дью петли гистерезиса ОА1ВС. Энергия в муфтах расходуется на внутреннее и внешнее трение при деформировании упругих эле­ментов.

Демпфирующая способность упругих муфт способствует сниже­нию динамических нагрузок и затуханию колебаний.

Каждая машина — это обычно слож­ная многомассовая система. Методы рас­чета колебаний таких систем изучают в специальных курсах. Для того чтобы выяснить, каким образом упругие муфты влияют на динамические свойства маши­ны, рассмотрим простую модель, схема которой изображена на рис. 17.11, и огра­ничим решение задачи дополнительными условиями, перечисленными ниже. На ри­сунке приняты обозначения: Jx — момент инерции масс привода (двигателя, пере­дачи и т. п.), приведенный к валу 1; J2 —

Момент инерции вращающихся масс исполнительного механизма, приведенный к валу 2; со и Т — угловые скорости и вращающие моменты на валах 1 и 2; С9 — жесткость муфты.

Дополнительные условия: 1) муфта имеет линейную характери­стику (Сф=Const), а жесткость всех других деталей машины велика по сравнению с С9. Поэтому в расчете колебаний учитываем только Сд,; 2) муфта обладает малой демпфирующей способностью, что позволяет не учитывать потери при составлении уравнений дви­жения; 3) машина оборудована двигателем, способным изменять момент Тг в широких пределах без существенного изменения угловой скорости. Поэтому в расчете сог принимаем постоянной. Практически последнее условие может быть применимо, например, для машин, оборудованных асинхронными электродвигателями. Частота вращения этих двигателей меняется незначительно при изменении момента в два раза и более. Условие со{ = Const равно­значно условию оо, т. е. приведению системы к одномас - совой.

Перечисленные условия позволяют рассматривать систему, по­казанную на рис. 17.11, как простейшую с одной степенью свободы. Размещая центр полярных координат на оси вала 1 и полагая, что эти оси координат вращаются с постоянной угловой скоростью Сои можно описать движение системы с помощью только одной

Переменной — угла закручивания муфты ср2. Уравнение движения массы J2

H^+C9Cp2=T2. (17.10)

В дальнейшем рассмотрим решения уравнения (17.10) для двух характерных случаев изменения нагрузки Т2: 1) нагрузка изменяется периодически в течение длительного времени; 2) изменения нагруз­ки имеют ударный характер.

Работа упругой муфты при периодически изменяющейся нагрузке. Периодическое изменение нагрузки распространено на практике. Такая нагрузка свойственна, например, поршневым машинам. Для краткости изложения допустим, что в частном случае с достаточной степенью точности нагрузка выражается с помощью гармонической функции в виде

Тг =70 + 7[35]2 Sin Cot. (17.11)[36]

График такой нагрузки изображен на рис. 17.12. Здесь Та2 и со — Амплитуда и круговая частота переменной составляющей нагрузки; Т0 — постоянная составляющая нагрузки (обычно Т0&ТЯ — номи­нальный момент). Далее обозначим ср2 = ср0+ср9 тогда

D2cp2/dt2=d2cp/dt29

Где сро — угол закручивания муфты, соответствующий постоянной составляющей нагрузки. Учитывая уравнение (17.11), после неслож­ных преобразований из уравнения (17.10) получаем

J2dzcpldtz + С> = Та2 Sin cot

Или

D2cp/dt2 + со2ср=Q Sin cot, (17.12)

Где

(17.13)

Как известно, уравнение (17.12) является уравнением простей­ших вынужденных гармонических колебаний. Общее решение этого уравнения имеет вид

Ср=A Sin coct+В Cos coct+[q/(co2 — со2)] Sin cot, (17.14)

Где А я В — постоянные коэффициенты; Сос — круговая частота свободных коле­баний. В уравнении первые два члена представляют свободные, а третий член — вынужденные колебания системы.

' В исследованиях длительных периоди­ческих колебаний свободные колебания обычно не учитывают, так как они быст­ро затухают даже при малом демпфиро­вании. В этоме случае

У с "

Tal = Ta2/[l-(CD/CDc)2].

Зависимость ТаХ от отношения со/сос выражается известной резо­нансной кривой (сплошная линия на рис. 17.13). Анализируя эту кривую, можно отметить: 1) Та — Та2 (по абсолютной величине)

Только в двух точках: при ш/шс=0 и при со/сос=у/2. Первая точка соответствует статической нагрузке (со = 0) или абсолютно жесткой муфте (шс=оо); 2) в промежутке 0<ш/шс<^2 всегда ТаХ > Та2 и при со/сос= 1 наступает резонанс (Та стремится к оо), сопровождающий­ся, как правило, поломкой машины; 3) при со/сос>у/2, ТаХ < Тл и при больших отношениях со/сос можно получить весьма малые ТаХ. На­пример, при ш/шс= 10 ТаХ = Ta2J99.

Разрешая неравенство со/сос>у/2 относительно жесткости муф­ты, получаем

Cg,<J2co2/2. (17.18)

Это значит, что при периодической нагрузке упругая муфта только тогда обеспечит более плавную работу механизмов машины по сравнению с соединением жесткой муфтой без учета упругости других деталей, когда ее жесткость удовлетворяет условию (17.18).

24-2973 3 77

При этом в период разгона и остановки машина проходит через критическую частоту вра­щения (резонанс).

Максимальные амплитуды в зоне резонанса устанавлива­ются не сразу, а нарастают по­степенно, поэтому разгон ма­шины, имеющей критическую частоту вращения, должен про­изводиться быстро. Для машин с критической частотой враще­ния целесообразно также при­менять демпфирующие упругие муфты. В этом случае резо­нансные амплитуды резко сни­жаются. Кривые амплитуд демпфирующих муфт показаны на рис. 17.13 штриховыми линиями. Здесь кривая 2 соответствует муфте с большим, а кривая 1 — с меньшим демпфированием.

Эффективным средством устранения вредных последствий резо­нанса является применение упругих муфт с переменной жесткостью (см. рис. 17.9).

Исследования показали, что для систем с такими муфтами вооб­ще не существует состояния, называемого резонансом, а амплитуда колебаний всегда имеет конечную величину. Это объясняется тем, что жесткость муфты изменяется с ростом амплитуды колебаний. Допустим, что система приближается к резонансу в точке А (см. рис. 17.9). При этом должны возрастать амплитуды колебаний. С ро­стом амплитуд изменяется жесткость муфты, т. е. частота свобод­ных колебаний системы. Система автоматически выходит из резо­нанса. Применять муфты переменной жесткости особенно целесооб­разно в тех случаях, когда частота вращения машины изменяется в широких пределах. При этом муфта постоянной жесткости не всегда способна обеспечить устойчивость машины во всем рабочем диапазоне частоты вращения.

Работа упругой муфты при ударных нагрузках. Приложение на­грузки к системе называют быстро нарастающим или условно ударным в тех случаях, когда нагрузка нарастает за промежуток времени, меньший полупериода свободных колебаний системы. Здесь целесообразно различать два основных случая ударного при­ложения нагрузки (рис. 17.14): 1) нагрузка после резкого увеличения остается неизменной в течение длительного времени; 2) резкое возрастание нагрузки сохраняется только в течение малого времени Ti (см. ниже).

Нарастание нагрузки и ее снижение могут происходить по - разному (рис. 17.14). В целях простоты и краткости изложения в дальнейшем рассматриваются только случаи с мгновенным нара­станием и снижением нагрузки (см. графики 1 и 2 на рис. 17.14). Полученные при этом общие выводы о влиянии упругих муфт на динамику работы машин принципиально справедливы и для других случаев ударного приложения нагрузки.

Первый случай. Нагрузка мгновенно нарастает и остается посто­янной длительное время (1, рис. 17.14). Этот случай характерен для машин, включаемых на полную нагрузку после холостого хода: прокатных станов, металлорежущих станков, толкателей нагрева­тельных печей и т. д. Уравнение движения массы с моментом инерции J2 (см. рис. 17.11) аналогично уравнению (17.12), в котором правую часть следует заменить постоянным приращением нагрузки Т2. Сохраняя прежние обозначения (17.13), получаем

D2<P/D/2 + A>C2<P = ?, (17.19)

Где q= T2/J2.

Общим решением уравнения (17.19) является

Q>=A sin coct+В Cos coct+Q/co2. (17.20)

Последний член правой части этого уравнения равен углу зак­ручивания муфты при статическом действии приращения нагруз­ки Т2. В этом легко убедиться, приняв во внимание зависимости (17.13).

Первые два члена уравнения представляют свободные колебания системы, вызванные ударным приложением нагрузки. Вследствие различного рода сопротивлений системы свободные колебания через некоторое время затухают и в уравнении остается только третий член. Однако на начальном участке колебаний после удара свободные колебания имеют существенное значение и поэтому не могут быть исключены из анализа, как это сделано при изучении установившихся колебаний, вызванных действием периодической нагрузки.

Произвольные постоянные АяВъ уравнении (17.20) определяют по начальным условиям. Эти условия со­стоят в том, что перед ударом допол­нительный угол закручивания муфты ср и скорость этого закручивания dcp/dt равны нулю. Итак, при /=0 Cp=0, D<P/D/=0.

Выполняя первое начальное условие подстановкой в уравнение (17.20), полу­чаем Продифференцировав t, c Уравнение (17.20) и выполнив второе Рис

Начальное условие, находим А = 0. При этом уравнение (17.20) при­нимает вид

Cp = (q/co[37])( 1 — Cos cot). (17.21)

Учитывая зависимости (17.13) и переходя к моментам, полу­чаем

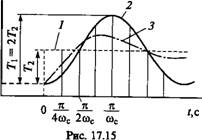
Тх = СрС9 = Т2( 1 - Cos coct). (17.22)

Графически уравнение (17.22) представлено на рис. 17.15, где 1 — линия нагрузки до муфты; 2 — то же, после упругой муфты без демпфирования; 3 — то же, после упругой муфты с демпфировани­ем. Из уравнения следует, что при ударном приложении внешней нагрузки Т2 максимальная нагрузка механизмов машины равна 2Т2 При T = N/Coc:

Max = 2 7*2.

При этом максимальная нагрузка механизмов не зависит от частоты свободных колебаний системы сос или от жесткости муфты. Она остается постоянной как при жесткой, так и при упругих муфтах, изменяется лишь плавность передачи этой нагрузки*.

Второй случай. Ударная нагрузка действует в течение малого времени Tx (2, рис. 17.14). В этом случае уравнение (П.22) справед­ливо только на отрезке времени /=0.../I. Анализируя это уравнение и график на рис. 17.15, можно отметить: 1) при Ti^N/Coc остается справедливым равенство TimBX=2T2; 2) при N/2Coc<Ti<N/Coc 2Т2> > Ттах> Т2 3) только при Ti < 7Г/2Шс можно ожидать Г1тах< Т2.

Таким образом, постоянную нагрузку, приложенную ударно, можно отнести к разряду длительных, если продолжительность ее действия больше или равна полупериоду свободных колебаний системы (период т=2П/сос).

Нагрузки, продолжительность действия которых меньше полу­периода свободных колебаний, отнесем к разряду кратковремен­ных. При кратковременных нагрузках после T=Tx система свободна от дополнительной нагрузки Т2. Для исследования дальнейшего движения системы (при T>T) используем уравнение (17.20), учиты­вая, что в этом случае Q=TjJ2=0. При этом получаем

<JP=^Sinroc/2+I*CosroC/2. (17.23) т

В уравнении (17.23) время t2 Отсчитывается от момента окон­чания действия нагрузки. Произ­вольные постоянные А и В опре- Tq Деляют из начальных условий. При /2=0 угол закручивания муф­ты ср и скорость этого закручива­ния dq>/dt определяют из уравне­ния (17.21), в котором следует принять T—T. Тогда получим:

1) Q>t2ss0=(q/co*) (1 — cos coctx)

2) (D(Jo/D/)R,=O=(q/coc) Sin шс/ь По первому условию из уравнения (17.23) находим

А по второму условию —

А== (д! со2) sin coct.

При этом уравнение (17.23) принимает вид

Q>=(q/co2) [sin coctx sin coct2+(1 — cos coct{) cos coct2]

Или

T = T2 [sin coct sin coct2+(1 — Cos coctx) cos a^/J. (17.24)

Уравнение (17.24) позволяет аналитически или графически опре­делить максимальные величины Т в зависимости от соотношения Tx и шс. Два таких графика даны на рис. 17.16: 1 —для Tx = я/(4шс), 2 — для /1=7г/(2шс). Графики позволяют отметить, что Т заметно уменьшается по сравнению с Тъ если tx меньше чем 1/8 периода свободных колебаний системы: *1<т/8 = я/(4шс).

Таким образом, правильным подбором жесткости муфт можно уменьшить вредное действие ударов на механизмы машины.

Третий случай. Рабочая машина (см. рис. 17.11) мгновенно оста­навливается вследствие чрезмерной перегрузки. Угловая скорость валов 1 и 2 до момента перегрузки была постоянной и равной со. После остановки (до выключения электродвигателя) систему нагру­жает пусковой момент электродвигателя В целях простоты решения полагаем, что пусковой момент двигателя равен его рабо­чему моменту Гн. При этом постоянную составляющую угла закру­чивания муфты q>О исключаем из рассмотрения, а движение массы
с Ji будет описываться уравнением свободных ко­лебаний (17.23) с началь­ными условиями: при t=0 q>=0, d(p/dt=coi.

Определив А и В для этих условий, получим В= =0, А = со1сос и

9=(Roi/Roc)Sinroc/. (17.25)

Учитывая, что сос = —[C9Ju получаем дополнительный момент, действующий на систему:

Тг = C9q> = (C^coicoc/coc) sin a>ct=Jl(D{(Dc sin roc/; (17.26) При / = я/(2гос)

Г1ти=Лш1шс. (17.27)

Уравнение (17.27) позволяет отметить, что дополнительный мо­мент, действующий на систему в результате ее внезапного торможе­ния, прямо пропорционален частоте свободных колебаний системы гос. Чем меньше жесткость муфты Сф при прочих равных условиях, тем меньше перегрузка механизмов машины. При жестких муфтах перегрузки могут достигать очень больших величин и вызывать поломку машины.

Рассмотренные выше характерные случаи работы упругих муфт позволяют сделать вывод о том, что выбор жесткости этих муфт следует производить в соответствии с характером ожидаемой дина­мической нагрузки машины. При этом в большинстве случаев прак­тики можно значительно уменьшить перегрузку механизмов.