ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

ОСНОВНОЙ ЗАКОН М. П. КОСТЕНКО

В работе [2], положившей начало частотному управ­лению, академик М. П. Костенко установил следующий закон управления амплитудой и действующим значением напряжения (в дальнейшем просто напряжения) в зави­симости от частоты: чтобы обеспечить оптимальный режим работы асинхронного двигателя при всех значениях часто­ты и нагрузки, относительное напряжение двигателя необ­ходимо изменять пропорционально произведению относи­тельной частоты на корень квадратный из относительного момента двигателя. Этот закон частотного управления можно записать уравнением

” но. ч

или в относительных единицах

Закон был получен в пренебрежении падением напря­жения в активных сопротивлениях статора и насыщением магнитной цепи.

Основополагающим в законе является то, что напряже­ние необходимо регулировать так, чтобы коэффициент ста­тической перегружаемости

оставался одинаковым при разных частотах. Так как мак­симальный момент изменяется пропорционально квадрату потока в воздушном зазоре Ф, то для этого необходимо, чтобы

Но в первом приближении

и' ^ ФТ, U" Ф'7'

откуда и следует основное

Положение вектора тока статора, а следовательно и ко­эффициент статической перегружаемое™, т. е. отношение максимального момента к моменту на валу двигателя при том же напряжении, будут неизменными при всех частотах и угловых скоростях двигателя, абсолютное скольжение имеет постоянное значение, а потери близки к мини­мальным.

Условия работы асинхронного двигателя в рассматри­ваемом режиме М. П. Костенко формулирует следующим 52образом [2]: «Если сконструировать асинхронный двига­тель для частоты fiHOM, момента М„ом и напряжения на за­жимах Uном и изменять затем при новом значении момен­та М напряжение U и частоту Д таким образом, чтобы удовлетворялось соотношение (2.1), то двигатель будет работать при практически неизменных cos ф, коэффициен­те перегружаемое™ и абсолютном скольжении, а его КПД будет определяться уравнением (2.2) и зависеть только от изменения частоты f/fПОм и практически не будет за­висеть от изменения момента на валу М/М

ном> если насы­щение магнитной цепи двигателя не слишком велико».

Закон Костенко говорит о том, как надо изменить на­пряжение, если двигатель будет работать не при номи­нальной частоте, а при новом, пониженном ее значении. Закон учитывает свойства нагрузки. Если она с уменьше­нием частоты также уменьшается из-за сопутствующего почти пропорционально частоте уменьшения угловой скоро­сти, то нет смысла сохранять поток двигателя на том же уровне. Его можно уменьшить настолько, чтобы только сохранить старый номинальный коэффициент статической перегружаемое™, т. е. запас статической устойчивости.

Уменьшение потока с уменьшением нагрузки при том же запасе устойчивости дает уменьшение потерь в стали двигателя и повышает экономичность привода с частотным управлением и часто меняющейся нагрузкой по сравнению с асинхронным двигателем при постоянной частоте.

Уменьшение потока с уменьшением момента, как извест­но, имеет место и у двигателей постоянного тока последо­вательного возбуждения.

Диапазон регулирования скорости вращения двигателя по рассматриваемому закону (2.1) ограничен сверху и снизу.

Верхняя граница определяется насыщением магнито- провода машины. С ростом отношения у /а растет магнит­ный поток машины и резко увеличивается ток намагничи­вания /0 ,, что и ограничивает допустимое значение этого отношения. Поэтому применение закона Костенко практи­чески ограничено нагрузками, не слишком превышающими номинальный момент двигателя.

Нижняя граница диапазона регулирования зависит от момента статического сопротивления при трогании двига­теля с места. Очевидно, при возрастании частоты и напря­жения от нуля двигатель будет неподвижен до тех пор, по­ка частота ротора, равная частоте статора (ротор неподви­жен), не достигнет такого значения, при котором момент двигателя превысит момент трогания неподвижного при­вода.

Практическое применение основного закона ограничи­вают трудности непосредственного измерения момента на валу двигателя.

НОМИНАЛЬНЫЙ ЗАКОН

В первое время практическое значение имел закон ре­гулирования напряжения пропорционально частоте:

U/fi=const, или у=а.

Нетрудно виДеІь, что StOT закон получайся Из зйкойа Костенко при постоянном номинальном моменте.

Этот режим близок к естественному режиму питания короткозамкнутого двигателя от синхронного генератора с постоянным возбуждением и от асинхронного преобра­зователя частоты. Его называли номинальным [3] потому, что табличные заводские

данные специальных серий г^л Х1 x rz4/fi

короткозамкнутых двигате­лей, выпускаемых промыш­ленностью, например роль­ганговых, указывались при­менительно к закону U—

= UH0 ма. При а = 1-ь-0,5

двигатель работает в усло­виях, мало отличающих­ся от номинальных. Но при дальнейшем уменьшении ча­стоты момент уменьшается и характеристики резко ухуд­шаются из-за снижения потока, обусловленного падением напряжения в активных сопротивлениях статора, как эго впервые было показано в [5]. Выяснение роли последнего и является основным результатом настоящего подраздели.

Согласно (2.2) выражение для тока статора (1.11) получает вид:

1 = ^номо[/"о+/^о(1 +Тг) +/'/г/р] • {г [/о+jxо(1 +тг)] —

— UV—го*о(ті + тг) ]а+ го+/*о(1 +Ti)] f^ct/p +

+/-1/-VP},

или, после сокращения на а:

/і==^ном { [/'0+/*0(1+Т2)+Г/2/Р] - Гі/о. [го+

+/*о (1 +т2) ] — [х2о%—jr0x0 (ті+т2) ] +

Н~ 1/о+/*о( 1+Ti) ] г'г/Р+гіг'г/сф}.

Этому уравнению соответствует схема замещения, по­казанная на рис. 2.1. Схема питается номинальным напря­жением, и все ее сопротивления, кроме активных сопро­тивлений статора и ротора, имеют постоянные значения такие же, как при номинальной частоте. Активное сопро­тивление статора изменяется обратно пропорционально параметру управления ct, а ротора — параметру нагруз­ки р.

Отсюда можно сформулировать следующее общее усло­вие работы асинхронного двигателя [5]: при управлении по номинальному закону U=UH0Mа и при пониженных ча -

etotax Двигатель имеет такие же значения токой, потоко! абсолютного скольжения (следовательно, р) и момента, какие он имел бы при номинальной частоте, но с увели­ченными обратно пропорционально частоте активными со­противлениями статора. Все мощности уменьшаются про­порционально частоте, а относительное скольжение увели­чивается обратно пропорционально частоте (и парамет­ру «).

Опуская вывод уравнений геометрических мест двига­теля в этом режиме, он изложен в работе [3], приведем только некоторые результаты, иллюстрирующие роль активного сопротивления статора.

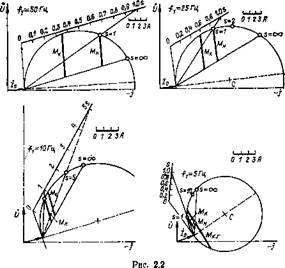
С изменением частоты круговые диаграммы деформи­руются тем больше, чем меньше частота. На рис. 2.2 по­казаны круговые диаграммы двигателя в номинальном ре­жиме при четырех значениях частоты: номинальной 50 Гц, а также 25, 10 и 5 Гц. Так как в этом режиме у=а, то со­гласно формулам (1.42) и (1.43) масштаб мощности изме­няется пропорционально частоте и cos сгі, а момента — S6только пропорционально cos сгі. Диаграммы построены для рольгангового двигателя типа АЗР 24/10-6.

Аналитические выражения характеристик в номиналь­ном режиме легко получить из общих формул § 1.1, под­ставив в них Y=a. В частности из (1.17) можно получить выражение для потока.

При уменьшении частоты статора поток снижается за счет падения напряжения в активном сопротивлении ста­тора тем больше, чем больше частота ротора. На рис. 1.3

Рис. 2.3

приведены кривые, показывающие изменение потока в за­висимости от частоты статора и ротора. Поток сравнитель­но мало меняется при частотах статора, близких к номи­нальному значению, потому что параметр р при нормаль­ных нагрузках мал (примерно |3<0,05), но уменьшается до нуля при всех значениях частоты ротора.

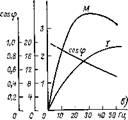
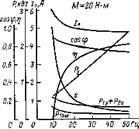
На рис. 2.3,а показаны характеристики двигателя АЗР 24/10-6: ток статора; потребляемая мощность; электриче­ские потери статора и ротора; коэффициент мощности и КПД в зависимости от частоты статора при постоянном мо­менте на валу М—20 Н-м. На рис. 2.3,6 показано для того же двигателя влияние частоты на пусковые характеристи­ки — момент, ток и коэффициент мощности.

Момент двигателя определяется общим выражением (1.20), если в нем принять у—а, или

Величины рКр и q определяются прежней общей форму­лой, так как они не зависят от параметра напряжения ■у

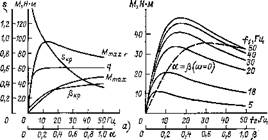
На рис. 2.4,а показано изменение в зависимости от частоты пара метров механической характеристики Мтах, ркр и q, а также макси мального момента в генераторной области МтахТ.

На рис. 2.4,6 приведено семейство кривых момента в зависимості от параметров абсолютного скольжения |3 при различных постоянны, значениях частоты статора и параметра а. Пунктирная кривая пока зывает изменение пускового момента Мп, т. е. момента при s=C а=р.

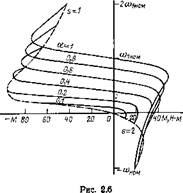
Ha рис. 2.5 показано семейство кривых момента в зависимости ог относительного скольжения s при разных значениях частоты статора. Максимальный момент в генераторной области больше, чем в двига­тельной, и в противоположность последнему возрастает с понижением частоты. Это явление обусловлено ролью активного сопротивления ста­тора и в уравнении момента (2.3) отражено через параметр q.

Зависимость момента от угловой скорости, которую легко получить из уравнения (2.3), подставив в него |3=sа, показана на рис. 2.6 се­мейством кривых при. разных значениях частоты.

Изложенные зависимости показывают, что номиналь­ный режим U~Unома для электроприводов с глубокой ре­гулировкой скорости и при скорости ниже 1/2—1/3 номи­нальной не эффектив^ц, Это и привело к многочисленным поискам «рациональ­ных» и «оптимальных» законов управления и способов их реализации, которые, как правило, требуют использования замкнутых цепей автоматического управления.

Таким образом, органический недостаток номинально закона управления напряжением заключается в уменьш пин потока с понижением частоты из-за падения напряж ния в первичных активных сопротивлениях двигате^' (в действительности к ним добавляются также и сопроти ления преобразователя частоты). Отсюда возникла нео ходимость изыскания такого закона регулирования напр, жения, при котором устранялось бы влияние этих сопр тивлений па поток двигателя. Для решения этой задач автор предложил регулировать напряжение на выводе двигателя так, чтобы падение напряжения в первичнь активных сопротивлениях точно компенсировалось [9]

Влияние активных сопротивлений г і на поток двигат ля будет компенсировано, если регулировать пропорциг нально частоте внутреннее напряжение эквивалентной схг мы замещения (см. рис. 1.1):

U'——l]ri=aU'noM, или у=а, (2.4

ГДЄ U'H0M^U' При U=Unом, / 1=/іном-

Очевидно, В ЭТОЙ формуле r-і должно учитывать сопрс тивленне только статора, если U — напряжение, измереь ное на выводах статора, и оно должно учитывать такж сопротивление преобразователя частоты, если U — внутреї няя ЭДС последнего.

Нетрудно видеть, что при регулировании напряжени по закону (2.4) сохраняет постоянное значение при все частотах полный поток двигателя

Фі =Ф + Фіз,

где Ф)8— поток рассеяния статора.

Действительно,

U'=llXl НОМ + £7hom) [■И — Сі'ФіномИ,

где индекс «ном» отмечает значения переменных при не минальной частоте.

На этом основании закон 1г — компенсации точнее на зывать законом регулирования напряжения, обеспечиваю' щим постоянство полного потока двигателя.

Закон регулирования с постоянным полным потоко> можно выразить через параметры машины следующим образом.

Действующее значение в обозначениях (1.10):

! ~т~+е2

Uf = aU " '

(і2 _|_ с2а2) —+ е2а2) г'+ 2г, а Г 2

При номинальном моменте p=sH0M и У,ои = ииш/ Ї (2.5)

(*2 + с2) 7r4-('i2 + e2) r' z/sm-A 4" 2 Г,

Искомый закон управления напряжением просто выра­жается через относительный параметр у.

U 10' + /■,/,!

I Г J -- TJ

и ном и 11

или, при использовании (1.11),

(/■, + /х, а) (Z0 +_52з)

/Л, а(г0+З3) +£022за

Отсюда в обозначениях И'кошеном получим искомый закон:

(Ь2 C2a2)P/r,2 + (d2 + Є2»2) - T-~2r, a

с2^г+е2т

Здесь £/'ном/£/ном — постоянный коэффициент, опреде­ленный уравнением (2.5).

Уравнения геометрических мест и характеристик дви­гателя можно получить из общих уравнений (см. гл. 1),

61

tAioM==t^ ном, Г=0, Y=a.

Поступая таким образом, из (1.11) получим:

/ —11' го + Іхо U + тг) +________ r't/$ /о Сї

ЛОМ [**,t +т,)Л-[Г,+ /X,(l+T,)jrvr ;

С исключением первичного сопротивления Гі параметр частоты а сократился, и благодаря этому геометрическим

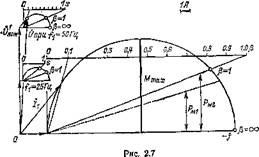
местом тока для всех частот является одна окружность (рис. 2.7). Уравнение вектора ее центра получим из (1.33)г подставив rj = 0, U НОМ — U ном и пренебрегая г2о<Сл:2о:

JU 2г0х — /JC0(I —f - 2т:)

Р и ном 2х20т(1 + х,) •

Из (2.6), полагая {3=0, найдем уравнение тока синхрон­ного холостого хода

І =Ur ---------------

о U н°«Г0 + /^о(1 +^і) ’

полагая |3=оо, получаем уравнение тока идеального корот­кого замыкания

j Tjr rbJr /*о (1 +

IJK — U ном _ x*#t + ;>оХо (Х] + х2)

и, полагая £=а (при 5=1), — уравнение тока короткого за­мыкания

/ r0 + jX о(1 +1;) + /•',/«________

^ ” ном —/г^,(х1+т1)] + [г, + /*,(1+х1)]г'|/“ •

Таким образом, в рассматриваемом режиме постоянного полного потока, или /^-компенсации, круговая диаграмма и все ее элементы, кроме точки короткого замыкания, не зависят от частоты. Точка короткого замыкания с изме­нением частоты леремещается по окружности. Ее положе­ние для любой частоты статора может быть найдено при помощи обычной шкалы скольжения. Так как в точке ко­роткого замыкания частота ротора равна частоте статора, положение точки короткого замыкания при частоте fi= =fіном определяется пересечением с окружностью луча, проведенного в деление шкалы s=a (рис. 2.7).

Построенная нами круговая диаграмма отличается от обычной круговой диаграммы при номинальных значениях напряжения и частоты только тем, что по положительной действительной оси направлен не вектор приложенного на­пряжения U, а вектор фиктивного напряжения U', вслед­ствие чего круговая диаграмма повернулась на соответ­ствующий угол по часовой стрелке.

Масштаб вторичного тока согласно формуле (1.41) по­стоянный (если пренебречь г2о в сравнении с х) ті2=тп(1 +ті).

Мощность измеряется отрезками, параллельными оси ординат, в масштабе, который изменяется строго пропор­ционально частоте:

mP=mlU'lI0MmIia.

Мощность электрических потерь в статоре можно учесть па круговой диаграмме специальной прямой, кото­рая строится следующим образом: через точку короткого замыкания при номинальной частоте p=s=l проводится прямая, параллельная оси ординат и ниже (или, условно, выше) оси абсцисс; на этой прямой находится точка, так, чтобы полученные отрезки были пропорциональны поте­рям короткого замыкания в роторе и статоре согласно от­ношению