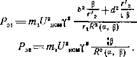ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
МОЩНОСТЬ, ПОТЕРИ, КПД
Первичная мощность, потребляемая двигателем,
Р=tn.UnQMlcos ф].
После подстановки Л из (1.11) и cos ф! из (1.16)
ь2 р— --d2 - g--f'ria
Р • п7 (І* Vа — -
гг цом| Г, Л2(а, Р)
Механическая мощность, получаемая ротором через воздушный зазор, т. е. мощность на валу плюс механические потери двигателя, согласно (1.21),
■Р^=.Ма)=.Л1а)іном(а—Р). (1.44)
Подставляя сюда М из (1.18), получим:
Л=Ж^ГІГ • (1
Для измерения мощности и потерь в относительных единицах удобно принять за базисную мощность вращающегося поля при номинальной частоте и номинальном моменте
Р оном —®1номМном. (1.46)
Тогда мощность в относительных единицах
^OHOM WjhomAIhOM
Механическая мощность в относительных единицах согласно (1.44) выразится просто:
Р2=(а—Р)ц, где fx — относительный момент (1.9).
Из (1.44) следует, что при любом конечном значении момента нагрузки М*Ф0, которому соответствует некоторое абсолютное скольжение Р=Р*, угловая скорость и полезная мощность равны нулю при частоте статора, отличной от нуля, но меньшей частоты ротора р*. Возникает «зона застоя» со=0 при а=р<;р*.
Пуск возможен только при а>р*.
Полезная мощность на валу двигателя меньше первичной мощности на полные потери в двигателе 2РП. Потери в двигателе суммируются из составляющих разной природы и определяются сложными расчетными формулами, основанными на эмпирических коэффициентах. Вопрос заметно осложняется при питании двигателя от преобразователей частоты из-за несинусоидальности формы кривых напряжения или тока. Поэтому при исследовании частотного управления применяют разные приближенные формулы потерь.
Потери в двигателе упрощенно можно представить суммой
ТіРп==Р а2~~Р с--Р мех - f - Рдо Ъ~-Ргар,
где Pal—электрические потери в обмотках статора; Рэ2—■ электрические потери в роторе; Рс — потери в стали статора; Рмех — механические потери; Рдоб — добавочные потери; Ртар — гармонические потери.
Потери в стали ротора малы и обычно ими пренебрегают.
Добавочные потери - учйтывйют ййхревые +окй 6 обідках, пульсационные потери в зубцах, потери в стали ротора.
Гармонические потери возникают от высших гармоник несинусоидальной формы кривых напряжения и тока при питании двигателя от вентильного преобразователя частоты.
В соответствии с эквивалентной схемой замещения рис. 1.1 потери двигателя можно учесть следующими приближенными формулами.
Электрические потери в обмотках статора и ротора
Раі=тіГіІ2і и Ру2—тіг'2І/22*=Щи<тМ§. (1.47)
Подставляя 1 и h из (1.13) и (1.14), получим:
|
|
Относительные электрические потери в роторе, учитывая (1.46)
|
|
Суммируя электрические потери, получим:
|
|
В относительных единицах, с учетом (1.12),
|
|
Потери в стали статора выразим приближенно следующим образом:
потери на гистерезис:
Рг=/СґФ2/інома,
от вихревых токов
Р вх=КвхФ2/21нома2.
Двигатель будет работать с минимальными электромагнитными потерями при любом моменте и
любой частоте статора, если менять напряжение и у так, чтобы абсолютное скольжение Р имело критическое значение ркрр, зависящее от частоты. Это положение, высказанное впервые в работе [3], было подтверждено другими авторами и дополнено учетом насыщения, которое влияет на ркрр [8 и др.].
|
о, ог о, оч - о, ов 0,08 о, ю ji |
|
Ряс. 1.8 |
|
|
|
|
|
<0 |
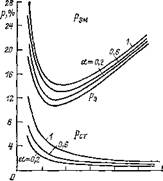
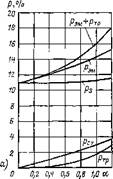
На рис. 1.8,а показаны в относительных единицах кривые потерь в зависимости от параметра абсолютного скольжения при трех значениях параметра частоты а=1; 0,6 и 0,2. Внизу построены кривые потерь в стали, рассчитанные по формуле (1.51). Их минимум лежит вне поля чертежа. Выше построена жирной линией одна для всех частот кривая относительных потерь в меди статора и ротора. Над ней — кривые суммарных электромагнитных потерь — в меди статора и ротора и магнитных — в стали. На рис. 1.8,6 показано влияние частоты на потери в режиме их минимума, т. е. при рКрр. Кривые построены также в относительных единицах. Верхняя кривая дает сумму всех потерь, включая механические.
Механические потери двигателя можно учесть, приняв, что они изменяются пропорционально угловой скорости ротора в степени 3/2, и пренебрегая скольжением:
Р тр ==Р тр. номО^,
где - Ртр. ном—Ртр при G—1. 44
Добавочные потери проще всего учесть как долю полезной мощности или как часть нагрузочных потерь. «Электромагнитный» КПД
*П - 2
|
Рг + Рэм |
Чэм р I р ' г2 Т ГЭМ
Здесь механическая мощность Р2 содержит и механические потери двигателя. Подставляя Р2 из (1.45) и Рэм из (1.52), получим:
|
|
При питании асинхронного двигателя от преобразователя частоты в нем появляются дополнительные «гармонические» потери вследствие несинусоидальности питающего напряжения. Эти потери в основном имеют характер джоулевых потерь, возникающих в статорных и роторных обмотках. Так как высшие гармоники токов пропорциональны отношению амплитуд гармоник напряжения к сопротивлениям рассеяния на соответствующих частотах, то гармонические потери можно считать пропорциональными квадрату потока основной гармоники [6, 8]. На этом основании гармонические потери можно выразить формулой
|
(1.55) |
Рrap—Кгар Ф®.
Коэффициент Ктар зависит от формы кривой напряжения данного конкретного преобразователя частоты, индуктивности рассеяния и от основной частоты fmом-
Согласно ГОСТ 16921-71 гармонические потери следует отнести к добавочным.
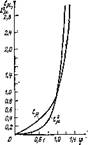
Приведенные здесь формулы потерь не учитывают их увеличения с насыщением машины. Увеличение потерь с насыщением определяется двумя факторами различной ттпироды: увеличением потерь в стали согласно (1.49) и увеличением электрических потерь в обмотках статора из-за быстрого возрастания с насыщением тока намагничивания. На рис. 1.9 показаны ток намагничивания и его квадрат в зависимости от потока, полученные по обратной характеристике холостого хода. Характер кривых очевиден. Ясно также, что главную роль в увеличении потерь играет не поток, а ток намагничивания, рост которого ограничи
вает допустимое увеличение потока и, следовательно, потерь в стали. Поэтому для исследования влияния насыщения на потери целесообразно разделить первичный ток на составляющую от нагрузки и составляющую намагничивания— ток возбуждения. Такое разделение соответствует схеме, замещения с вынесенной на внешнем выводе намагничивающей ветвью и строго доказано в [6].
|
Рис. 1.9 |
Для упрощения анализа воспользуемся приближенным соотношением
|
|
Действительно, из (1.13) и (1.14) приближенное значение тока возбуждения
|
Iі —І* — Ґ J 0 * 1 J о |
/^номтУ ( г Р. 1 т . о Р ^
лхгі V •к+^.т+2х'-,)
отличается от точного значения. (1.15) только последним членом в скобках.
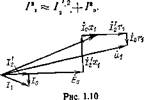
Принятому приближению соответствует векторная диаграмма двигателя рис. 1.10.
При слабом насыщении, т. е. на линейном участке характеристики холостого хода, электрические потери в обмотке статора от тока возбуждения пропорциональны квадрату потока
Л>в — mirіЛ> = ffVi У=тіГі )V
Ров=/СэвФ2,
или
|
CJr |
|
-)• |
|
K3S = mtrt |
|
Для учета насыщения электрические потери возбуждения удобно объединить с потерями в стали в общие потери 46 |
где
возбуждения [8j:
Рш = (Кэ>+K„s) ф* = К, ф*. (1.56)
С увеличением потока потери возбуждения быстро растут. Это возрастание потерь в [8] предлагается учитывать показателем степени у потока и>2, который рассматривается как некоторый эмпирический переменный коэффициент. При сильном насыщении он может превышать к=5.
В общем случае
P*=KJF.
Коэффициент потерь возбуждения удобно использовать в относительных величинах:
ks=Кв/Кв. ном,
где /Св, ном — коэффициент потерь возбуждения при номинальном режиме.
Таким образом, суммарные потери в обмотках двигателя разделили на нагрузочные потери в обмотках статора и ротора от тока ротора и электрические потери на возбуждение потока
Рэ1 + - Рэг = Рэ. нат + Рэв-
Электрические потери в роторе в области реальных нагрузок, когда скольжение мало, можно на основании приолиженной формулы (cos<p2«l) выразить как
( М У >—-г*(сгф) >
где
C2=7,im2pk2W2-10_6.
d^L=-2KH§-+K^~l +2КгарФ=0.
Коэффициенты Кн, Кв и /Сгар могут быть определены экспериментально или расчетом по известным, в частности номинальным, значениям удельных потерь, момента и потока
Коэффициенты Потерь Кн и /Св зависят С>т Частоты. И* значения при частоте а можно вычислить по номинальным значениям при а=1
Подставив в условие минимума потерь (1.58) значения коэффициентов из (1.59), (1.60) и используя (1.55), получим это условие в нормализованном виде
|
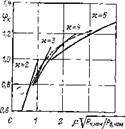
На рис. 1.11 показаны в относительных единицах кривые зависимости критического значения потока фк от произведения относительного момента на корень квадратный из отношения нагрузочных потерь к потерям возбуждения при фиксированных (номи- (Р нлом/ степени 4 и 5. некото - которая |
|
|
|
Рис. 1.11 |
Пунктиром показана рая средняя кривая, близка к кривой при и=4 и соответствует достаточно широкому диапазону изменения переменных. Этот график позволяет сделать принципиально важный вывод — оптимальное по минимуму потерь значение потока быстро растет с увеличением момента двигателя, что качественно согласуется с основным законом Костенко (см. § 2.1).
Зависимость абсолютного скольжения р0пт от момента при оптимальном по минимуму потерь значении потока Фк, с учетом насыщения, можно получить следующим путем.
|
|
Исследование уравнения (1.62) показывает, что с ростом насыщения при больших показателях степени и параметр р несколько возрастает с увеличением момента.
Описанный метод расчета потерь и их оптимального значения был проверен расчетами на ЭВМ на многих двигателях различных типоразмеров с хорошими результатами [8}, которые оказываются достаточно точными при изменении момента от половины номинального до двух - и трехкратной величины.
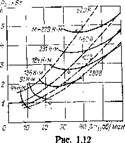
На рис. 1.12 приведены кривые потерь в зависимости от абсолютного скольжения, рассчитанные на ЭВМ по точной схеме замещения при постоянном вращающем моменте (сплошные линии) и при постоянном питающем напря
жении (пунктир). Кружками показаны четыре точки, рассчитанные по изложенной выше методике.
Кривые рассчитаны для трехфазного двигателя, имеющего следующие номинальные данные: мощность 22 кВт, напряжение 460 В, частота 60 Гц, число пар полюсов р=3.