ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

КРУГОВЫЕ ДИАГРАММЫ

Наглядное и информативное представление о характе­ристиках асинхронного двигателя дает метод векторных уравнений и его графическая интерпретация в виде геомет­рических мест—множества точек, описываемых на пло­скости векторами состояния при изменении параметров: нагрузки—скольжения р и управления — частоты а и на­пряжения v [3]. Метод векторчых уравнений Может стать 25полезным подспорьем при аналитических исследованиях и расчетах на цифровых ЭВМ и сократить машинное время. Геометрические места показывают поведение асинхронного привода по всему пространству состояний и позволяют вы­брать минимальное число вариантов, заслуживающих рас­чета па ЭВМ. С другой стороны, геометрические места — годографы состояния в функции параметров а, р и у могут быть рассчитаны на ЭВМ, а их изображения выведены на графопостроители или дисплеи для наблюдения, исследо­вания и корректирования. Однако этот вопрос, относящий­ся к машинному проектированию, еще мало разработан.

При частотном управлении построение круговых диа­грамм на плоскости осложняется появлением двух новых независимых переменных — частоты а и напряжения у.

Вектор проводимости статора G будет описывать на комплексной плоскости кривые, зависящие от двух пара­метров: частоты ротора а и частоты ротора или абсолют­ного скольжения р.

Из этих кривых можно выделить геометрические места двух видов.

1. Семейство геометрических мест проводимости (тока) но параметру управления а при различных постоянных значениях параметра нагрузки, т. е. абсолютного скольже­ния Р:

в ПРИ Р = constСемейство геометрических мест проводимости (тока) по параметру нагрузки |3 при различных постоянных зна­чениях параметра управления a: при a=const. Это

семейство отличается от обычных круговых диаграмм при постоянной частоте, очевидно, только параметром. Вместо относительного скольжения s они имеют параметр нагруз­ки р, пропорциональный абсолютному скольжению:

при a=^c°nst - с1-23)

К первому виду геометрических мест следует отнести и кривые, описываемые вектором центра окружностей про­водимости (тока), поскольку эти кривые не зависят от па­раметра нагрузки р, но зависят от параметра управле­ния а.

При переходных электромеханических процессах ча­стотного управления векторы токов будут описывать на комплексной плоскости кривые, для которых семейства геометрических мест обоих указанных видов будут слу­жить сеткой своеобразных криволинейных координат.

Практическое значение геометрических мест постоян­ной частоты статора, т. е. обычных круговых диаграмм, не требует пояснений. Геометрические места постоянного аб­солютного скольжения полезны в двух отношениях. Во-пер - вых, они дают характерные точки круговых диаграмм, необходимые для построения последних при любом задан­ном значении частоты статора, т. е. параметра управле­ния а; во-вторых, они наглядно показывают влияние изме­нения частоты статора на характеристики двигателя и на деформацию круговых диаграмм.

Поле обоих семейств геометрических мест a=const и p=const может дать полное и наглядное представление о поведении двигателя в любых режимах частотного управ­ления.

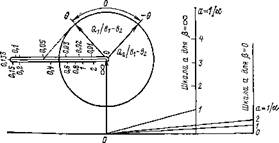
Для практического применения геометрических мест необходимо не только построить их кривые согласно век­торным уравнениям, но и указать на них распределение точек соответствующего параметра: a — для геометриче­ских мест постоянного абсолютного скольжения p=const и параметра р — для геометрических мест постоянной ча­стоты статора a=const.

Для геометрических мест a=const распределение то­чек параметра нагрузки р может быть установлено с по­мощью шкал, которые строятся аналогично шкале сколь­жения обычной круговой диаграммы.

Распределение точек параметра частоты статора а на геометрических местах постоянного абсолютного скольже­ния |3=const может быть определено при помощи шкал прямого параметра а или обратного параметра 1/а=а.

Эти шкалы в нашем случае проще всего строить, исхо­дя из следующих соображений.

Положение точки на прямой проводимости (тока) Gі может быть определено фазой вектора тока этой точки ф или дополнительным углом а—п/2—ф, отложенным от оси абсцисс. Угол определяется выражением

где /а и /^—-активная и реактивная составляющие тока. В общем случае

(

откуда находим уравнение Шкалы

р = 4- 5-+ (Р - № = Р - jR - fSa..

Шкала проходит через точку S оси ординат под углом о о к оси абсцисс. Масштаб шкалы определяется аргу­ментом

tgOi=(P+S)/R,

так как ее нуль лежит на оси ординат.

Рассмотрим сначала геометрические места постоянного абсолютного скольжения.

Для упрощения, как и в § 1.2, будем пренебрегать по­терями в стали, т. е. допустим, что го=0 (уравнения с уче­том Го имеются в [3]).

Общее уравнение проводимости (тока) первичной цепи статора (1.22) запишем в виде

—' = г,/У+£«' (1>25)

Здесь обозначено:

H=r/2/$-i~jxo (1 +тг);

_S=jx0 ( 1 - f" Ті) r'2/P—Х2оТ.

При дальнейшем увеличении р конец вектора р воз­вращается обратно по тому же отрезку (нижняя половина эллипса) до точки, в которой |3=оо и которая совпадает с начальной точкой 0=0.

Распределение точек параметра а по окружности р= =const может быть установлено при помощи шкал пара­метра а. Уравнение для этих шкал можно получить из уравнения (1.25), записав его в виде

0,=

Г і + £(Р) я rt+Fxa + jFyV - ’

где

■ХрТ + /(1 +*і)гУЕ + Iх о(1 + Х2)

Отсюда находим выражение для углового аргумента шкалы из условия tg o=ctg Ф, где ф — фазовый угол век­тора проводимости:

Рг* + Г 1 Fx + r, а

и в развернутом виде

xVVp Т'1 [Л ovi т *21 - Г'2 /Р J,, nrv,

Хо [х20х(1 +Х2) 4- (1 + т,)г22/З2]

Шкала проводится параллельно оси ординат на произ­вольном от нее расстоянии. Нуль и единица шкалы опре­деляются лучами, проведенными под углом к оси абсцисс*,' о при а=0 и о при а= 1 (а=1/а).

Найдем теперь окружности p=const для двух гранич­ных случаев: Р=0, т. е. окружность идеального холостого хода, так как при р=0 и s=0, и окружность Р=оо, т. е. окружность идеального короткого замыкания, так как при Р=оо и s=oo.

Вектор центра окружности идеального холостого хода получим из (1.27) подстановкой р=0:

Ро= 1 /2л*і.

Шкала параметра частоты статора может быть опреде­лена непосредственно из выражения (1.25) для проводи­мости при Р=0 тангенсом ее углового аргумента

tg3o== х„(1 +Ч)« = *0(1+*|) * (1‘30)

Для окружности идеального короткого замыкания р = = оо, = 1 /р = 0 аналогичным путем получим:

Роо=1/2^ = Р„-

Уравнение тангенса шкалы параметра bполучим из (1.29), подставляя Ь0 = 0:

tg0 =/l(1 +Slg. (1.31)

6 оо x0z ' '

Окружности идеального холостого хода и идеального короткого замыкания совпадают (с точностью до потерь в стали), но имеют разные шкалы параметра частоты.

Абсцисса центра эллипса равна большой полуоси Rci - Центр эллипса и его малая полуось находятся на действи­тельной положительной полуоси, а большая ось проходит параллельно мнимой оси координат. Нетрудно видеть, что малая полуось эллипса равна радиусу окружности |3=0 и Р=оо, т. е. центры этой окружности и эллипса совпадают (рис. 1.6).

Шкалу параметра частоты а для разметки точек на эллипсе центров можно построить по угловому аргументу вектора эллипса из (1.35). Аргумент этого вектора о опре­деляется только числителем (1.33). На этом основании, отсчитывая о от мнимой отрицательной полуоси, получим:

(1.38)

Радиус окружности проводимости определяется из (1.23) общим выражением

AL — K

K*L—KL* ’

которое после подстановок дает:

Радиус окружности Rc уменьшается прямо пропорцио­нально частоте статора а.

Для построения круговых диаграмм нет необходимости вычислять радиус окружности проводимости, поскольку эта окружность определяется своим центром и любой из точек

На рис. 1.6 построены на основании изложенных здесь соотношений геомет­рические места постоянного абсолютного скольжения: окружности р=0, р = оо, р=1 {f2 = f 1нок) > ЭЛЛИПС центров, а также их шкалы частоты статора а. Постро­ения выполнены по число­вым данным, приведенным ниже.

Для построения круговой диаграммы проводимостей (или тока) при некотором достоянном значении часто - ciatopa па эллипсе центров и окружности $=6, оо с по­мощью соответствующих шкал параметра а строятся точ­ки центра, 0=0 и оо (s=0, оо). Центр окружности пер­вичного тока можно построить по двум точкам s=0 и s= = 00, ие строя эллипса, но имея шкалу его параметра. Для этого достаточно точки s=0 и s—oо соединить хордой (т. е. линией моментов) и из ее средней точки провести нормаль до пересечения с лучом, соединяющим начало ко­ординат с соответствующим делением а=а* шкалы эллип­са. Точка пересечения даст центр окружности тока при а=а*.

Точки р=0 (s=0) и (3=оо (s=oo) определяют окруж­ность первичного тока и линию момента s=0, s=00. Поло­жение точки короткого замыкания s=l (а=р), определя­ющей положение линии полезной мощности, т. е. хорды 5=0, s=l, проще всего установить по отношению элек­трических потерь ротора и статора при коротком замыка­нии s=l.

Это отношение, приближенно:

С понижением частоты оно гиперболически возрастает, потому что потери в статоре не равны нулю при а=0 (на постоянном токе).

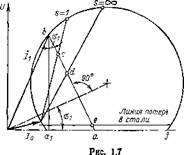
Для построения точки короткого_з_амыкания таким спо­собом (рис. 1.7) нужно на прямой ab, произвольно прове­денной по направлению измерения мощностей, т. е. нор­мально вектору центра окружности проводимости (первич­ного тока), построить отрезок cd=ed/Kp. Очевидно, точки с, s=0 и искомая точка короткого замыкания s=l будут лежать на одной прямой. После этого строится обычным методом шкала параметра скольжения как прямая, прове­денная параллельно линии моментов до пересечения с про­должением линии полезной мощности. Эта точка пересе­чения даст единицу шкалы скольжения, а точка пересече­ния шкалы с касательной к окружности в точке s=0 даст пуль шкалы скольжения.

Таким образом, определены все основные элементы окружности проводимости (тока) для любой частоты.

Некоторые построения можно упростить. Построение окружностей постоянного абсолютного скольжения встре­чает затруднения из-за большого радиуса (на рис. 1.6 пунктиром показана в нижнем левом углу окружность то - 3* 35 ка при номинальной частоте). Но точки этих окружностей легко рассчитать по формуле, вытекающей из уравнения окружности в декартовых координатах:

У = Уц + VR* — C*i,+ •*)*•

Здесь R — радиус окружности, г/ц — ордината ее цен­тра, отсчитываемая по действительной положительной по­луоси, принятой за ось у, хц — абсцисса, отсчитываемая по оси х, направленной по отрицательной мнимой полуоси.

Определение на построенной круговой диаграмме вели­чин двигателя — токов статора и ротора, подводимой и otj даваемой мощностей, потерь, момента, cos <р, КПД и сколь­жения выполняется, так же как и на круговых диаграм­мах, при постоянной частоте.