ПОЛУЧЕНИЕ КОМПОЗИЦИОННЫХ. ГРАНУЛИРОВАННЫХ МАТЕРИАЛОВ. В ПЛАНЕТАРНОМ ГРАНУЛЯТОРЕ
Условие адгезии упругопластических сферических тел
Исследована зависимость силы адгезии от силы сжатия двух упругопластических сферических частиц. Принято, что до достижения условия пластичности на всей площади контактной площадки деформация происходит по закону Герца. Площадь контакта после достижения условия пластичности на всей контактной площадке находится из условия, что отношение удельного давления к напряжению текучести в момент, когда достигается условие пластичности на всей контактной площадке, остается неизменным при увеличении силы сжатия частиц [26]. Сила адгезии равна своему теоретическому максимуму - произведению площади контакта и напряжения текучести. Решение является приближенным, предназначено для оценки интенсивности агломерации сыпучего материала в построенной математической модели окатывания частиц в планетарном грануляторе.
Применение гранулированных материалов является для некоторых технологий обязательным условием. В планетарном грануляторе за счет центробежных сил создаются значительные давления, что при одновременном скатывании позволяет гранулировать пластичные материалы без добавления связующих [27].
Для изучения процессов гранулирования упругопластических материалов, когда адгезия обусловлена силами сжатия частиц [1], необходимо знать зависимость величины контактной площади и силы адгезии взаимодействующих тел от силы их сжатия. Исследовать взаимодействие тел сложной формы затруднительно из-за многочисленных вариантов контактов. Во многих работах по математическому моделированию движения гранулированных сред авторы принимают частицы материала сферической формы для упрощения исследования поведения гранулированных сред [28]. Полученная зависимость будет использоваться в математической модели окатывания
сыпучего материала в планетарном грануляторе с целью получения данных о зависимости интенсивности агломерации от параметров процесса окатывания. В математической модели принимается сферическая форма взаимодействующих тел. Высокая точность зависимости силы адгезии от силы сжатия не обязательна, так как в процессе расчета в математической модели происходит большое количество взаимодействий частиц. На интенсивность агломерации влияет изменение количества слипшихся частиц, то есть изменение сил адгезии в общем объеме сыпучего материала.
Приняты следующие допущения для упрощенного решения поставленной задачи. Тела деформируются в пределах упругой деформации по закону Герца [29]. До достижения условия пластичности на всей площадке контакта деформация также происходит по закону Герца. При достижении условия пластичности по всей площадке контакта и дальнейшем увеличении силы сжатия частиц отношение удельного давления к напряжению текучести остается неизменным [26]. Адгезия имеет место в точках пятна контакта, где интенсивность напряжений больше напряжения текучести. Сила адгезии равна своему теоретическому максимуму, то есть произведению площади контакта, где выполняется условие пластичности, и напряжения текучести [1].
Радиус пятна контакта по закону Герца
a = 1,109^FRp /E, (3.1)
где F - сила сжатия, Н;
E - модуль упругости, Па. Приведенный радиус
![]()
![]()
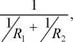 (3.2)
(3.2)
где Ri - радиус первого тела, м;
R2 - радиус второго тела, м.
Нормальное давление в центре контакта по закону Герца
P0 = 0,3883jFE2 /R], (3 3)
Главные напряжения в центре контактной площадки [29]:
_3 = - ро; _2 = _1 = -0,8P0- (3-4)
Главные напряжения по периметру контактной площадки:
ст3 = 0; ст2 =-0,133P0; ст1 = 0,133P0. (3.5)
Согласно теории Герца нормальное к контактной площадке давление распределяется так, что плоская эпюра, показывающая распределение нормальных давлений вдоль любого диаметра контактной площадки, ограничена полуокружностью [29], и его максимум равен P0
ст3 = —Va2 - r2, (3.6)
a
где r - удаление от центра контактной площадки, м.
Принимается, что ст1 и ст2 изменяются линейно при удалении от центра контактной площадки к ее периметру:
Ст2 = P01 0,8 - 0,677(3.7)
![]() ст1 = P0| 0,8 - 0,933— І.
ст1 = P0| 0,8 - 0,933— І.
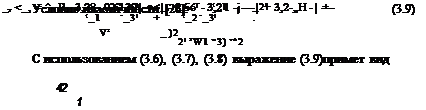
a
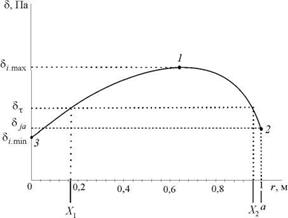
Для зависимости _, от r при a = 1, показанной на рис. 3.1, характерны следующие точки.
Максимальная интенсивность напряжений при r = 0,6576a
_,.тах = 0,5028P 0. (3.11)
Минимальная интенсивность в центре пятна контакта при r = 0
Интенсивность напряжений при r = а
ст1а = 0,2304P 0. (3.13)
Минимальная сила сжатия сферических частиц, необходимая для начала их прилипания и образования адгезионной связи, находится следующим образом. Из формул (3.3), (3.11) следует, что
ст,. max = 0,5028P0= 0,5028 • 0,3880^FE2/R2p. (3.14)
Из выражений (3.3), (3.10), (3.14) получаем:
Сила сжатия частиц, при которой достигается принятое условие пластичности по периметру контактной площадки, находится аналогично. Из выражений (3.3), (3.10), (3.13) получим:
Сила сжатия частиц, при которой достигается принятое условие пластичности по всей контактной площадке, определяется из выражений (3.3), (3.10), (3.12):
При силе F, большей чем F3, на всей контактной площадке достигается условие пластичности, поэтому теория Герца здесь не может быть применена, так как описывает лишь упругую деформацию.
Принимается приближенно, что отношение удельного давления к сопротивлению деформации (напряжению текучести) остается постоянным при F > F3, и равно таковому при F = F3 [26]. Это соотношение при F = F3 находится далее. Удельное давление равно среднему нормальному давлению [26].
Интегрированием выражения (3.6) получаем зависимость удельного давления от P0:
Минимальная интенсивность напряжений при F = F3 на контактной площадке определена из выражения (3.12):
CTi. mm = 0,2 P 0 = а Т. (3.19)
Отношение удельного давления к сопротивлению деформации (напряжению текучести) согласно выражениям (3.18), (3.19):
— = 3,3333. (3.20)
СТт
Площадь контакта определяем из выражения (3.20):
![]()
![]() (3.21)
(3.21)
Сила адгезии, согласно выражению (3.21),
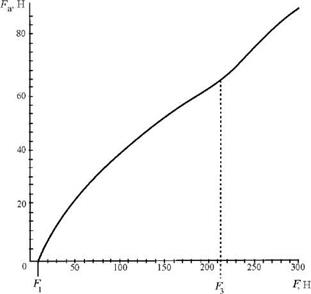
Зависимость силы адгезии от силы сжатия показана на рис. 3.2. Сила адгезии имеет следующую зависимость от силы сжатия частиц [30]:
1) при F < Fi
Fa = 0; (3.23)
2) при F1 < F < F2
Fa =°тп(*22 - X2), (3.24)
где x1, x2 - удаление от центра контактной площадки г, при котором выполняется равенство (3.25) с подстановкой формул (3.1), (3.2), (3.3), (3.10);
а т = <3j; (3.25)
3) при F2 < F < F3
Fa = атп(а2 - x2) = атп(у.0&(Рір /E)2 - xf); (3.26)
4) при F > F3
![]() Fa = 0,3F.
Fa = 0,3F.
|
Рис. 3.1. Интенсивность напряжений |
|
Рис. 3.2. Зависимость силы адгезии от силы сжатия частиц |