ПОЛУЧЕНИЕ КОМПОЗИЦИОННЫХ. ГРАНУЛИРОВАННЫХ МАТЕРИАЛОВ. В ПЛАНЕТАРНОМ ГРАНУЛЯТОРЕ
Математическая постановка задачи
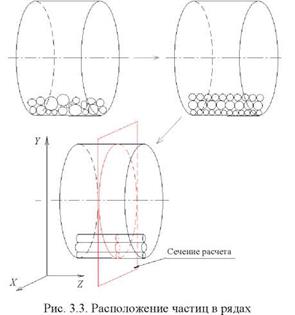
Для расчета только в двух измерениях приняты следующие допущения. Предполагается, что сферические частицы равного диаметра располагаются в ряд, причем ось данного ряда параллельна оси барабана, а длина ряда равна ширине барабана (рис. 3.3). Таким образом, все частицы располагаются и двигаются в барабане рядами и не имеют перемещений в измерении, параллельном оси барабана. Частицы в рядах не контактируют между собой, но имеют жесткую связь. Масса ряда частиц равна сумме масс составляющих его частиц, количество контактов между двумя рядами частиц равно наибольшему количеству частиц в одном из рядов, направление нормальной силы реакции всех контактов частиц перпендикулярно осям рядов частиц. Таким образом, получена возможность расчета трехмерных объектов при вычислениях только в двух измерениях.
|
|
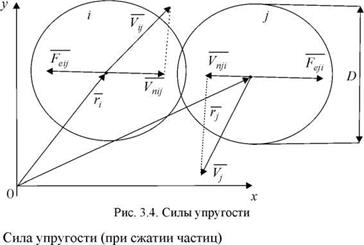
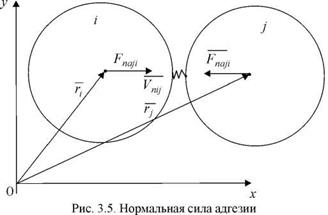
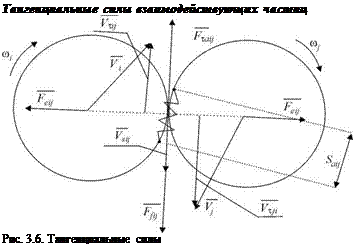
Нормальные силы взаимодействия частиц Силы упругости, нормальная сила адгезии и тангенциальные силы представлены соответственно на рис. 3.4, 3.5, 3.6.
|
FeiJ = 8(R. + Rj - r] - r )nLE. (3.28) |
|
|
F
nviJ 1/ m, +1/ m,
Нормальная сила реакции адгезионной связи (при растяжении связанных адгезионной связью частиц)
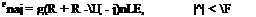
![]()
 |
= 1
Скорость скольжения
= Kj-Кл-®iRi -®jrj. (3 31)
Сила трения скольжения
- У - і і
F. =u(F.. +F, V. <V, (3.32)
fij eij nvij V S1J s. min
s. min
Fj =v(Fey + Fnvj), VJ > Vs. mln. (3.33)
Минимальная скорость скольжения для определения силы трения скольжения
VS min = Vd/20. (3.34)
Линейная скорость вращения поверхности барабана
WdDd
2
Тангенциальная сила реакции адгезионной связи
|
|
||

Образование и разрыв адгезионных связей Нормальная сила сжатия
![]() F = F + F..
F = F + F..
n eij nvij •
Максимальное нормальное напряжение на контактной поверхности взаимодействующих сфер
an = 0,3883j FnE2 (і/ Ri + 1/ Rj )2. (3.38)
Максимальное напряжение на контактной поверхности
аг = 0,5028 • 0,388^ FnE2 ( + 1/Rj )2. (3.39)
Предполагается, что адгезия возникает в тех местах контактной площади соприкасающихся частиц, где интенсивность напряжений превышает предел текучести материала. При достижении предела текучести материал течет, заполняя пустоты, образованные неровностями поверхностей частиц. После заполнения материалом всех пустот поверхности частиц сближаются настолько, что проявляются силы молекулярного взаимодействия, обуславливающие появление адгезионной связи между частицами. При этом адгезия равна когезии.
Предположительное условие появления адгезии в точке площади контакта частиц:
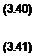
![]() ai >ат.
ai >ат.
Условие образования адгезионной связи для сфер:
Fn > F0,
где
![]() ______________ ат _____________
______________ ат _____________
(0,5028 • 0,388)3E2( + 1/Rj)
Fei + Fnvi > 134,685 E2 ((+1/R]) .
Условие образования адгезионной связи для двух рядов сферических частиц с длиной L:
3
![]()
![]() Feij + Fnvij > 134,685 ^ 2------
Feij + Fnvij > 134,685 ^ 2------
У 4 E 2 (1/ ( +1/ Rj ) 2 Ri
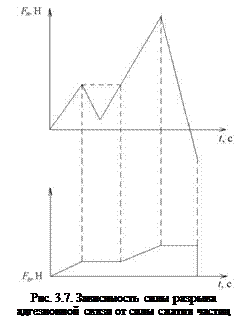
Предполагается, что сила разрыва адгезионной связи двух частиц пропорционально зависит от максимальной силы их сжатия. Определяющей является максимальная нормальная сила сжатия частиц за время их взаимодействия после появления адгезионной связи. Пример зависимости силы адгезии от силы сжатия частиц представлен на рис. 3.7.
 |
Сила разрыва адгезионной связи
F = K„Fn.„. (3.45)
Предполагается, что
Ка = const 0 < Ка < L (3.46)
При моделировании принято:
Ка = 0,3.
|
|
|
|

![]()
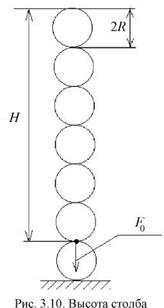
![]() Для оценки физических свойств материала введен показатель H, равный высоте столба одинаковых сферических частиц, при которой достигается условие возникновения адгезионной связи между нижней частицей и частицей, находящейся над ней.
Для оценки физических свойств материала введен показатель H, равный высоте столба одинаковых сферических частиц, при которой достигается условие возникновения адгезионной связи между нижней частицей и частицей, находящейся над ней.
Сила тяжести столба частиц равна минимальной силе сжатия сферических частиц, необходимой для образования адгезионной связи:
G = F0. (3.47)
Радиусы частиц столба равны:
R = R = Rj. (3.48)
a: R
![]() (0,5028 • 0,3880)3 E2
(0,5028 • 0,3880)3 E2
|
||
|
||
|
||
Высота столба частиц не зависит от размера частиц:
8(0,5028 • 0,3880)3 E W
Принимается, что в слое сыпучего материала, состоящем из сферических частиц с различными размерами, с высотой слоя, равной H, для нижних частиц также выполняется условие возникновения адгезионных связей.
Для гранулятора со стационарной осью, при скорости вращения менее критической, высота слоя, при которой выполняется условие возникновения адгезионных связей для нижних частиц, определяется по формуле
8(0,5028 • 0,3880)3 E 2p%g'
При планетарном вращении барабана гранулятора возникают центробежные ускорения, в несколько раз большие ускорения свободного падения, в этом случае выражение (3.52) примет вид
Зст3 g
Hp = т ^-------------- = Н. (3.53)
р 8(0,5028 • 0,3880)3 E 2p%ac ac
Центробежное ускорение
ac =®p (Rp + 0,2Dd/2). (3.54)
Множитель 0,2 введен в связи с тем, что при планетарном вращении расстояние между центром планетарного вращения и центром тяжести материала обычно больше радиуса планетарного вращения примерно на 20 % от радиуса барабана, так как под действием относительного вращения барабана материал отклоняется от линии, проходящей через точки Ср, Cd (рис. 4.17), на угол 45-80° (рис. 418).
С учетом (3.54) выражение (3.53) запишется следующим образом:
p 8(0,5028 • 0,3880)3 E2pna2p (Rp + 0,1Dd)'
Условие, при котором частицы, находящиеся на дне окатываемой массы в барабане планетарного гранулятора, слипаются между собой под действием сжимающих сил, выражается неравенством
Юр > . (3.56)
р 8(0,5028 • 0,3880)3 E 2р n(Rp + 0,lDd )Hp
Высота слоя материала в барабане зависит от его заполнения сыпучим материалом.
Теоретически можно подобрать параметры гранулирования без добавления связующего для любого материала в планетарном грануляторе, однако планетарная скорость вращения барабанов и размеры гранулятора могут быть увеличены лишь до определенных пределов, обусловленных техническими причинами.
Предполагается, что максимально возможная планетарная скорость вращения гранулятора равна 2000 об/мин или 209 рад/с. Максимально возможный радиус планетарного вращения l м, максимальный диаметр барабана при этом 0,8 м.
Таким образом, максимально возможное центробежное ускорение
acmax = 2092(l + 0,2• 0,8/2) = 47175 м/с2. (3.57)
При этом высота необходимого слоя материала в планетарном грануляторе
£ 98
Hp = Н = Н = 0,0002077Н. (3.58)
р ac 47175
Hp при диаметре барабана 0,8 м может быть максимум 0,2 м.
Параметр Н, зависящий только от физических свойств материала, при этом равен
H 0 2
![]()
![]() _ ____ р__ _
_ ____ р__ _
= 0,0002077 = 0,002077
Для материалов, имеющих параметр Н менее 963 м, имеется возможность гранулирования в грануляторе с описанными выше параметрами.
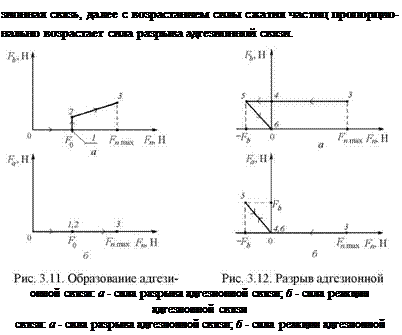
При моделировании предполагается следующая последовательность образования и разрушения адгезионной связи (сдвиг отсутствует). Две частицы сжимаются под действием внешних сил, нормальная сила сжатия частиц достигает в точке 1 (рис. 3.11, а, б) величины F0 - минимальной силы сжатия сферических частиц для образования адгезионной связи, - в точке 2 (см. рис. 3.11) возникает адге-
После точки 3 (см. рис. 3.11) сила сжатия частиц уменьшается (рис. 3.12), однако сила разрыва адгезионной связи остается постоянной до точки 5 (рис. 3.12). В точке 5 сила разрыва адгезионной связи становится равна силе растяжения адгезионной связи частиц, и адгезионная связь разрушается. Сила реакции адгезионной связи равна нулю от момента образования адгезионной связи (точка 2 на рис. 3.11) до момента возникновения растяжения адгезионной связи (точка 4 на рис. 3.12), далее сила реакции равна по модулю силе растяжения. После разрыва адгезионной связи сила реакции адгезионной связи становится равной нулю (точка 6 на рис. 3.12).
Условия разрыва адгезионной связи:
1) при растяжении
Fb < VFna + 3FTa ; (3.60)
2) при сжатии
Fb <А/F2 + 3Fx2a. (3.61)