ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ В ГЕЛИОСИСТЕМЕ С ЕСТЕСТВЕННОЙ ЦИРКУЛЯЦИЕЙ ТЕПЛОНОСИТЕЛЯ
Естественная циркуляция теплоносителя используется в небольших солнечных установках.
Математическая модель представлена нестационарными уравнениями энергии, движения и сплошности для всех элементов установки с соответствующими начальными и граничными условиями, обеспечивающими сопря
жения этих элементов. При этом учитываются наиболее существенные характеристики тепловых и гидродинамических процессов, протекающих в системе в целом и в каждом её элементе. Процесс расчёта включает ряд этапов: тепловой расчёт солнечного коллектора, тепловой расчёт бака-теплоаккумулятора совместно с соединительными трубопроводами, определение расхода теплоносителя при его естественной циркуляции [68].
Температура прозрачного покрытия Тс=Тс(х, х,у) определяется уравнением
8сРсСс^ = ^ас(?;-Гс) + С/с0(Гс-Г0). (1.140)
дх
При расчете коэффициента тепловых потерь U учитывалось излучение пластины и стекла (прозрачной изоляции), свободная конвекция между пластиной и стеклом в воздушном зазоре, теплопроводность через теплоизоляцию ит. д.
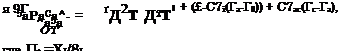 |
|
Температура пластины абсорбера описывается уравнением:
Начальное условие для уравнений (1.140) и (1.141) имеет вид Тй=Тс= Т0 при т = 0 .
Граничные условия для области пластины ozxz—t ozyiLCK можно представить следующим образом:
дТ N
—— = 0 при х =—; дх 2
ЯГ
2Я. а8а-ті = а»я^.(Гв ~ТЖ) при х = 0. дх
Здесь предполагается, что тепловой поток равномерно распределен по периметру трубы солнечного коллектора,
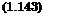 ВТ дТ
ВТ дТ
—- = 0 при у = 0, —- = 0 при у = ігк.
ду ' ду
Температурные поля Тс=Тс(х, х,у)и Т&=Тй(х, х,у)определяются в области 0 < т < т„
N
0<ж<—, 0<y<LCK. (1.144)
2
где tc - продолжительность светового дня.
Для типовой конструкции солнечного коллектора выполняется неравенство LCK « N/2, поэтому представляется возможность провести усреднение температурного ПОЛЯ по координате х, т. е. свести задачу к одномерной, полагая
Та(х, у)=— f Ta(z, x,y)dx; N J
![]() Тс(х, у)=^~ j Тс(х, x,y)dx. N J
Тс(х, у)=^~ j Тс(х, x,y)dx. N J
В гелиосистемах с естественной циркуляцией обычно осуществляется ламинарный режим течения жидкости, для которого справедливо соотношение аж =4,36 Я, ж/гіж.
С учетом этого соотношения и приведенных выше граничных условий можно записать:
![]() 8сРссс^ = ийС(Тй-Тс) + ис0(Тс-Т0). от
8сРссс^ = ийС(Тй-Тс) + ис0(Тс-Т0). от
8.РА^ = *А0-18,7^-(Т.-Тя) + Р-ЩТл-T0)) + Uac(Tc-TJ. (1.146)
Индексы усреднения в этих формулах опущены. Система уравнений (1.145) и (1.146) решалась при следующих условиях:
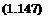 Та = Т0=Т прит = 0
Та = Т0=Т прит = 0
граничные:
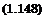 -^- = 0 приу = 0яу = LCK
-^- = 0 приу = 0яу = LCK
Температурное распределение в жидкости, протекающей по трубам коллектора, описывается дифференциальным уравнением конвекции:
![]() С1 яф
С1 яф
+ сж—^г = 13,7^*(7;-Тж). (1.149)
п ду
Тепловой расчет солнечного коллектора заключается в решении уравнений (1.145), (1.146) и (1.149) при начальных и граничных условиях:
Я'г яу
ТЛ = ТЖ=Т0=Т при т = 0; = 0 при у = 0, = 0 при у = LCK. ц 150)
В уравнениях (1.140)—(1.150) приняты обозначения: Гс, 8С, рс, сс - соответственно температура, толщина, плотность и удельная теплоёмкость прозрачного покрытия; т - время; Та - температура пластины поглощающего элемента (абсорбера); Т0 - температура окружающей среды; U — коэффициент тепловых потерь, Ui = X. J 54 (X - теплопроводность; 5 - толщина пластины); LCK, N - размеры пластины; 'кж - теплопроводность жидкости (теплоносителя); <1ж - диаметр трубопровода для теплоносителя; Gx - расход теплоносителя; Тж - температура теплоносителя.
Математическая модель бака-теплоаккумулятора (БТА) учитывает эффект перемешивания стратифицированных слоев жидкости в результате конвекции при подводе горячего теплоносителя. Уравнение сохранения энергии для БТА имеет вид:
7бта=7о при т = 0.
Граничное условие:
зт
^БТА = ^ж. под (х>Ьг) при 2 = 0; >-ж —= С/бтао(?бта - Т0) при z - НБТА (1.152)
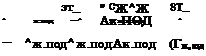 |
||
Температура жидкости в подъемном трубопроводе Гж. под =Гж. под(*>У) определяется уравнением:
Начальное условие:
7,ж. под=7,о при т = 0. Граничное условие:
![]() 7,ж. под=7,ж(т, А;к) при У = 0.
7,ж. под=7,ж(т, А;к) при У = 0.
Температура жидкости в опускном трубопроводе Гж. оп =7,ж. оп(т, У) определяется уравнением:
Начальное условие:
Тж. оп=Т0 При Т = 0.
Граничное условие:

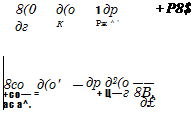 |
||
Для определения расхода жидкости по замкнутому контуру воспользуемся уравнением Навье-Стокса для одномерного течения жидкости по трубе:
Применяя уравнение к поперечному сечению трубы, получим:
где со = со(т, В), р = р(т, %) - средние по сечению скорость и давление жидкости; %ст - касательное напряжение к стенке трубы.
Здесь учтено, что на оси трубы (£ = 0)
![]()
![]() дсо т = ц—
дсо т = ц—
%
а на стенке трубы (£ = d/2)
5со
Индекс усреднения в дальнейшем опущен. Поскольку движение жидкости в результате естественной конвекции происходит по замкнутому контуру гидравлической системы установки, то произведем интегрирование уравнения (1.158) по этому контуру:
Проанализируем величины, стоящие в правой части уравнения (1.159). Можно показать, что
^ст(^ = - р»^ЕА/ »
(
где hi — удельные потери напора на преодоление всех сил сопротивления на і-м участке гидравлического контура. Рассмотрим интеграл
ТЛ г* м ч ч
Как известно, разность между объемной силой и силой давления при естественной конвекции жидкости можно принять равной g(p-p0). Таким образом
Рж**-|| Y^ = -<j> £(рж - Ро)sin (Рж - Ро)sin »
где ф£, - угол наклона контура dE, к горизонтали.
Проанализируем величины, находящиеся в левой части уравнения (1.159). Так как скорость жидкости при естественной циркуляции мала,
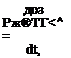
![]() скоростным слагаемым пренебречь.
скоростным слагаемым пренебречь.
Первое слагаемое в левой части уравнения (1.159) представим в виде:
С доз,, доз,
В результате уравнение (1.159) примет удобный для практических расчетов вид
Записывая уравнение неразрывности для всех элементов гелиоситемы
(СК, БТА, опускного и подъемного трубопроводов) и учитывая соотношение
-Нтэгрд.011
—:1±^«------------- , первое слагаемое представим:
/БТА fsc. on
Вводя коэффициент объемного расширения, первое слагаемое в правой части уравнения (1.160) запишем в виде:
^ск
—'^(P*-Po)sintPds = P' J [гж (у)-Гж. под(іж. ппд)]SincpCKrfi/- П 161)
Ро о v • /
где фск - угол наклона солнечного коллектора; перепадом температур по длине соединительных трубопроводов пренебрегаем.
Последний интеграл в правой части уравнения (1.161) является движущей силой для свободной конвекции в БТА, приводящей к образованию замкнутых токов жидкости внутри бака, поэтому данным интегралом можно пренебречь.
Записывая выражение для гидравлических потерь, пренебрегая местными сопротивлениями по сравнению с сопротивлением по длине и учитывая, что для ламинарного режима течения, который, как правило, имеет место при естественной циркуляции теплоносителя, коэффициент сопротивления по длине определяется соотношением А/ = 64/Re, второе слагаемое в правой части в формуле (1.161) запишем в виде:
|
^-**Ьов |
 |
|
Здесь учтено, что ^ ТА ^БТА ^ж. оп 1ж. оп. В результате уравнение движения жидкости примет вид:
Начальное условие: Ож = 0 при т = 0.
В уравнениях (1.151)-(1.163) кроме указанных в тексте, приняты обозначения: ТБТД - температура жидкости в баке-аккумуляторе; fBTA - поперечное сечение ВТ А; иБТА0 - основные тепловые потери в БТА; НБТД - высота БТА; а - скорость; ^ - естественные координаты для движения жидкости по трубе; g - ускорение свободного падения; р - динамическая вязкость; уж - кинематическая вязкость жидкости; Р' - угол наклона поверхности к горизонту.
Таким образом, гелиосистема с естественной циркуляцией описывается следующей системой уравнений, с учетом начальных и граничных условий:
для солнечного коллектора:
"„РА - ь = (Д - Tc)+Uc0(Tc-Т0); ах
с)Т dzT X
6яряся —— = ХЯ8„ —f-13,7—247; - Тж) + (<7- (7,(71 - TQ)) + UaJTc-71);
a a dx a a dy2 N a ж г a 0 ac 0 a
ndl nn dT G dT
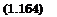 c p Чж-од + r = 13,71 (T - T );
c p Чж-од + r = 13,71 (T - T );
4 dx n dy ‘
Tc = T& = Тж = T0 при x = 0;
![]() ■ — 0, Тж - Тж ПГ1Д(ЬЖ под) при ї/ = 0;
■ — 0, Тж - Тж ПГ1Д(ЬЖ под) при ї/ = 0;
п г
—- = 0 При!/ = £ск.
ву
- для бака-аккумулятора (БТА) с подъемным и опускным трубопроводами:
![]() , 9гБТД ртбта -
, 9гБТД ртбта -
РжСж/бТА - + Сж^ж _ “ Аж? БТА - 2 +(
OX OZ OZ
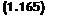 „ г агж.„,л, „ агж...д
„ г агж.„,л, „ агж...д
Ржсж 4 Ьж. под ^ + ^жЧк^ж. под Qy -
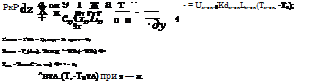 |
~ ^Ж. ПОД^Ж. ПОдАк. ПОД (^Ж. ПОД А ) j
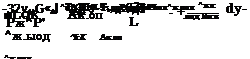 |
|
— уравнение движения:
=0 при т = 0.
Расчет проводился методом конечных разностей по неявной схеме Кранка - Николсона, которая является абсолютно устойчивой.