ТОНКОПЛЕНОЧНЫЕ. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ. НА ОСНОВЕ КРЕМНИЯ
Заряд в полупроводнике
В аморфном кремнии квазиуровни Ферми отстоят от границ разрешенных зон более чем на 2kT. Для такого невырожденного полупроводника выполняется статистика Больцмана и концентрацию свободных носителей можно определить по формулам
п = nc exppfn - ec)];
p = nv exP[(Ev - Ep)].
Для оценки заряда носителей, захваченных на состояния в запрещенной зоне рtrap, используются модели доноро - и акцептороподобных состояний, а также состояний амфотерного типа в щели подвижности a-Si:H. Как правило, принимается, что состояния на хвосте зоны проводимости являются акцептороподобными: они отрицательны, когда заняты электроном, и нейтральны, когда свободны от электрона. Состояния на хвосте валентной зоны имеют донороподобное поведение, доноро - и акцептороподобные состояния на хвостах зон — экспоненциальное распределение.
Принимается, что состояния, обусловленные оборванными связями, имеют амфотерное поведение, т. е. могут находиться и в доноро - и в акцептороподобном положении. Это объясняется тем, что они могут быть в трех зарядовых состояниях: положительно заряженном (свободны от электрона), нейтральном (на них находится один электрон) и отрицательном (заняты двумя электронами). В данном случае оборванная связь приводит к появлению двух энергетических уровней в щели подвижности: уровень Е+/0 соответствует переходу +/0, а уровень Е0/- — переходу 0/-. Расстояние между двумя уровнями соответствует энергии, которую необходимо затратить, чтобы на уже занятом состоянии появился второй электрон (корреляционная энергия ЕЦ). В модели структур энергетических зон в аморфных полупроводниках Мотта и Дэвиса принимается, что состояния, обусловленные оборванными связями, имеют гауссово распределение.
В этом случае заряд на доноро - и акцептороподобных состояниях равен соответственно
Ес
Pd = q I N(Е) [1 - f (Е)] dE;
Еу
Ес
Pa = - q I N(Е) f (Е¥Е,
Еу
|
|
|
|
|
|
 |

цесса захвата и два — эмиссии (рис. 7.4): r, Г4 — скорости захвата на уровень Et электрона и дырки соответственно; Г2, Г3 — скорости эмиссии электрона и дырки.
В табл. 7.1 охарактеризованы все процессы эмиссии и захвата электронов и дырок на доноро- и акцептороподобные состояния (см. рис. 7.4). В табл. 7.1 использованы следующие обозначения: Ta, Td — акцепторо - и донороподобные состояния соответственно; vth — тепловая скорость носителей; Nt — концентрация ловушек; , а° — сечение захвата ловушки
для электрона и дырки соответственно; e - , е0Р — коэффициент эмиссии
для захваченного электрона или дырки соответственно. Индексы «+», «О» и «-» означают зарядовое состояние ловушки.
Таблица 7.1
|
Процессы эмиссии и захвата электронов и дырок на доноро - и акцептороподобные состояния
|
В условиях термодинамического равновесия в соответствии с принципом детального равновесия ri = Г2 и Г3 = Г4. При этом вероятность заполнения состояния описывается функцией Ферми — Дирака:
f = [1 + exP(Et - ef)]-1.
Отсюда коэффициенты эмиссии равны
Общая скорость рекомбинации составляет
R = гі - Г2 = Г3 - Г4. (7.8)
Принимая во внимание это выражение, а также выражения для скоростей эмиссии и захвата, получаем функцию занятости:
Используя выражение (7.8) и подставляя в него выражения для Г1, Г2, Г3 и Г4, определяем эффективность рекомбинации:
![]() R 2 + 0
R 2 + 0
Лг _ ~^thanap
Nt
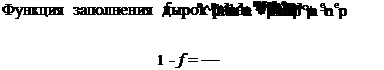 |
|
Тейлор и Симмонс показали, что выражение (7.9) может быть аппроксимировано выражением
Выражение (7.10) может быть преобразовано следующим образом:
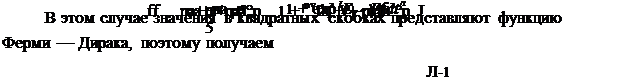
-1-1
Квазиуровень Ферми для захваченных электронов равен
![]() nan + pa p
nan + pa p
Nc a+
Аналогично функция заполнения дырок
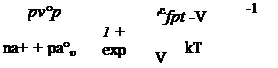 |
||
|
||
|
||
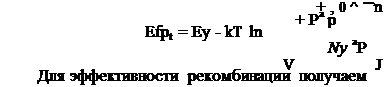 |
||
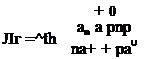 |
|
|
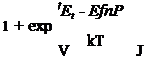 |
||
|
||
 |
||
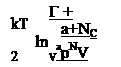 |
||
|
||
 |
В табл. 7.2 даны пояснения к процессам, представленным на рис. 7.5.
Таблица 7.2
Процессы эмиссии и захвата электронов и дырок
на состояниях амфотерного типа
|
Процесс |
Переход |
Скорость процесса |
|
Захват электрона |
D ++ e ^ D0 |
ri = nvth°+ndbf+ |
|
Эмиссия электрона |
D0 ^D++e |
r2 = en NDBF 0 |
|
Захват электрона |
D0 + e ^ D~ |
r3 = nvth°n, NDBF 0 |
|
Эмиссия электрона |
D - ^ D0 + e |
r4 = e~n NDBF- |
|
Захват дырки |
D0 + h ^ D+ |
r5 = pvth°°pNDBF 0 |
|
Эмиссия дырки |
D + ^ D0 + h |
r6 = e+pNDBF+ |
|
Захват дырки |
D - + h ^ D0 |
r7 = pvthF~pNDBF - |
|
Эмиссия дырки |
D0 ^D-+h |
r8 = epNDBF 0 |
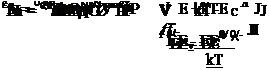 |
В табл. 7.2 D означает оборванную связь, F — функцию занятости, индексы «+», «0» и «-» — зарядовое состояние оборванной связи. Коэффициенты эмиссии в этом случае равны
Функции занятости для зарядовых состояний:
![]() _______ P0 Р~________ ;
_______ P0 Р~________ ;
N+P - + P0P - + N+N0 ’
_______ N+Р~________ ;
N+P - + P0P - + N+N0 ’
N 0 N+
![]() N+P ~ + P° P ~ + N+N 0
N+P ~ + P° P ~ + N+N 0
+ + . + 0 0.0 - - . - 0 0.0 где N = щи°п + ep; N = nvth^n+ep; P = pvth° p+en; P = pvth° p+en.
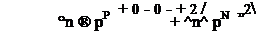
Используя эти выражения, определяем эффективность рекомбинации: Лг = r1 - r2 + r3 - r4 = vth (Рп - ni У
Средний заряд, приходящийся на одну оборванную связь, равен
Q = q ( f + - f -).