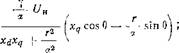СИСТЕМЫ ЧАСТОТНОГО УПРАВЛЕНИЯ СИНХРОННО-РЕАКТИВНЫМИ ДВИГАТЕЛЯМИ
Схема замещения синхронно-реактивного двигателя при частотном управлении
В основу исследования рабочих характеристик СРД при частотном регулировании положена его схема замещения.
При исследовании рабочих характеристик при частотном управлении сделаны допущения, аналогичные допущениям, которые принимаются для анализа поведения СРД при фиксированной частоте. Важнейшие из этих допущений состоят в следующем:
1) распределение м. д. с. и потокосцеплений по расточке статора принимается синусоидальным, влияние пространственных высших гармонических магнитного поля не учитывается;
2) влияние временных высших гармонических магнитного поля не учитывается;
3) магнитная цепь двигателя принимается ненасыщенной, насыщение учитывается путем выбора соответствующих значений параметров;
4) параметры не зависят от токов, скорости вращения, а активные сопротивления — от температуры.
Для исследования поведения СРД при частотном управлении воспользуемся теорией этого двигателя, разработанной для фиксированной частоты [JI. 4—10].
Как известно, для фиксированной частоты напряжений питания СРД, работающего в синхронном режиме, предложены две схемы замещения [Л. 4—7]. В одной из них параметры зависят от временного угла 0 между вектором напряжения сети V и вектором поперечной составляющей тока, а в другой — от угла бр'между вектором напряжения, уравновешивающего первую гармонику э. д. с., индуктируемую в статоре потоком реакции якоря, и вектором по-
|
|
|
|
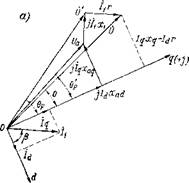
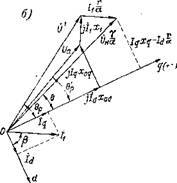
Рис. 1. Векторные диаграммы синхронно-реактивного двигателя: а — при фиксированной частоте; б — при переменной частоте.
перечной составляющей тока (рис. 1, а). При условии, что число пар полюсов СРД р= 1, угол 0Р' можно рассматривать как пространственный угол между осями магнитного поля основной гармоники в воздушном зазоре и ротора. Эти углы определяются из соотношений (см. векторную диаграмму рис. 1, а):
О' =arctg(jfe_V V Id%ad /
где xq=xaq + xu xd—xad-hxi — индуктивные синхронные сопротивления соответственно по поперечной и продольной осям при номинальной частоте fH; Xad, Xaq — ИНДуКТИВНЫе СОПрОТИВЛЄНИЯ, обу - словленные потоком реакции якоря по продольной и поперечной осям машины при номинальной частоте; х — индуктивное сопротивление рассеяния фазы обмотки статора при номинальной частоте; г — активное сопротивление фазы обмотки статора; /<ь —
проекции вектора тока на продольную и поперечную оси.
Определим вначале схему замещения СРД, работающего в синхронном режиме при переменной частоте напряжения питания, с параметрами, зависящими от временного угла 0.
Уравнение равновесия напряжений при фиксированной частоте для одной фазы статорной обмотки СРД в установившемся режиме работы может быть записано так:
U — jldxad Н qxaq “і - І І Xх! b ^lr >
где U — напряжение сети; I — ток статора.
|
(4) |
Учитывая, что вектор U образует с поперечной осью ротора q угол 0 (см. векторную диаграмму рис. 1, а), уравнение (3) при любом заданном значении частоты питающего напряжения можно представить в виде
|
U cos 0 = Id-2nfLd - f Iqr j U sin 0 — lq-2-r. fLq — Idr, j
|
Разделив обе части уравнений (4) на f/fn, где f — текущее значение частоты напряжения питания СРД, a fH — номинальное, и обозначив f/fn = a и U/Un = у, где а и y — параметры, характеризующие частоту и величину напряжения питания СРД, получим уравнения равновесия напряжений при частотном управлении (см. рис. 1, б) :
—U H COS 0 IdXd -Ig — a 1 a
UK sin 0 = Iqxq — Id — - •
Эти уравнения отличаются от уравнений (4) тем, что в них значения подведенного напряжения UHyfa и активного сопротивления г/а при частотном управлении являются переменными величинами и изменяются обратно пропорционально относительной частоте а. Подведенное напряжение, кроме того, изменяется пропорционально параметру относительного напряжения у.
Из уравнений равновесия напряжений (5) можно получить выражения для продольного и поперечного токов:
|
|
|
Id |
|
|
|
Вектор полного тока фазы обмотки статора |