Система электропривода

БЛОК РЕГУЛЯТОРОВ СИСТЕМЫ ПРЯМОГО УПРАВЛЕНИЯ МОМЕНТОМ

Как было указано выше, блок регуляторов в системах прямого управления моментом содержит дискретную и непрерывную часть. Дис­кретная часть блока регуляторов построена на основе регуляторов ре­лейного вида. Релейные системы автоматического регулирования, как известно [4], являются к системам прерывистого действия, а, следова­тельно, относятся к нелинейным системам. В таких системах моменты времени перехода релейных регуляторов из одного устойчивого поло­жения в другое определяются внутренними свойствами самой системы. В то же время релейные системы обладают перед непрерывными тем преимуществом, что здесь не требуется высокая точность стабилизации параметров для соблюдения требуемой зависимости между входным и выходным сигналами (они более “грубые”) - [13].

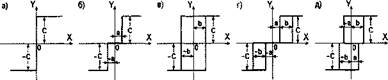
Статические характеристики типовых релейных элементов имеют вид, показанный на рис.2.2.

Y = C*sigllX (2.1)

Релейное звено с зоной нечувствительности (рис.2.2,б) представ­ляет собой трехпозиционное реле. У этого звена три устойчивых состоя­ния, включая нулевое. Уравнения для релейного звена с зоной нечувстви­тельности имеют вид:

(2-2)

С при Х>а; Гл

0 при-а<Х<а;

О при - а <Х<а; или Y = і

[С • signjX - а) цш£Х > а.

С при Х<-а. k '

Трехпозиционное релейное звено с зоной нечувствительности и с гистерезисным допуском (рис.2.2,г) описывается следующими уравне­ниями:

Настройка релейных регуляторов в системах прямого управления моментом сводится к определению ширины гистерезисной петли у двух­позиционных реле, ширины гистерезисной петли и зоны нечувствитель­ности - у трехпозиционных реле и коэффициентов усиления линейных, безынерционных датчиков обратных связей. Сигнал с выхода релейного регулятора представляет собой последовательность прямоугольных им­пульсов с единичной амплитудой (С = 1). Частота следования импульсов определяется только внутренними параметрами динамических звеньев контура.

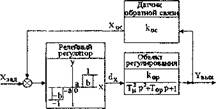
В системах прямого управления моментом наиболее широкое рас­пространение получили релейные регуляторы с характеристиками вида рис.2.2,в и рис.2.2,г, поэтому далее будут оценены свойства замкнутых контуров регулирования с релейными регуляторами этого вида. В про­стейшем случае, когда в контуре используется релейный регулятор вида рис.2.2,в, а объект регулирования представляет собой апериодическое звено первого порядка, структурная схема контура регулирования имеет вид, представленный на рис.2.3.

Совместное решение уравнений 2.6 и 2.7 позволяет отыскать квазиоптимальную настройку контура с гистерезисным релейным регу­лятором.

В более сложном случае, когда в контуре используется релейный регулятор вида рис.2.2, г, а объект регулирования представляет собой апериодическое звено второго порядка, структурная схема контура регу­лирования имеет вид рис. 2.5.

Условием устойчивой работы контура с релейным регулятором является поддержание релейного элемента в автоколебательном режиме [4]. В противном случае система теряет работоспособность.

Внешний регулятор в системах прямого управления моментом - линейный. Как правило, это регулятор пропорционально-интегрального вида [38]. Однако, известны системы, в которых используются П - регуля­торы и ПИД - регуляторы. Внешний контур регулирования в системах DTC замкнут по частоте вращения двигателя. Сигнал обратной связи может быть получен путем прямого измерения частоты вращения с помощьювращающегося датчика скорости любого вида, либо может быть вычис­лен в вычислителе ненаблюдаемых координат на основании информа­ции о фазных напряжениях и токах асинхронного двигателя. В последнем случае несколько сужается диапазон регулирования частоты вращения и ухудшается точность регулирования из-за вычислительных ошибок.

Настройка параметров регулятора скорости в системах DTC может варьироваться в широких пределах для достижения желаемого качества переходных процессов, а также для обеспечения допустимой величины статической ошибки регулирования при использовании П-регулятора ско­рости. В то же время быстродействие системы от настройки регулятора скорости зависит мало. Быстродействие системы в целом определяется, главным образом, частотой автоколебаний релейного гистерезисного ре­гулятора внутреннего контура.

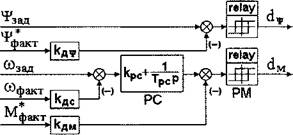
Таким образом, структурная схема блока регуляторов системы прямого управления моментом выглядит всегда одинаково, как показано на рис. 2.7. Различия состоят только в выборе вида линейного регулятора скорости и конфигурации релейных гистерезисных регулятором потокос­цепления статора и электромагнитного момента двигателя.

Структурная схема реализована с помощью стандартных динами­ческих и нединамических блоков. Здесь и далее нединамические звенья в структурных схемах обозначаются так, как это принято в среде Simulink системы MATLAB. На схеме рис.2.7 блок, реализующий релейный эле­мент с зоной нечувствительности и гистерезисным допуском обозначен “relay”. При моделировании в среде MATLAB релейный элемент вида рис.

2.2, г реализуется с помощью двух параллельно включенных релейных элементов [9] - рис. 2.8.

Рис. 2.8. Структурная схема трехпозиционного релейного звена с зоной нечувствительности и с гистерезисным допуском для моделирования в среде MATLAB.