ОБЩИЙ ПОДХОД К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СИСТЕМ DTC
Система прямого управления моментом асинхронного электропривода включает в себя несколько функциональных блоков, каждый из которых может быть реализован разными способами. В связи с этим представляется целесообразным следующий подход к построению математических моделей систем DTC. Предварительно в виде структурных схем, реализованных с помощью элементарных динамических звеньев, отдельно разрабатываются модели всех функциональных блоков системы. Поскольку каждый функциональный блок имеет несколько вариантов реализации структурных схем, воспроизводящих каждый функциональный блок, тоже будет несколько. Полученные структурные схемы функциональных блоков объединяются в так называемые субсистемы. Терминология (subsystem) заимствована в системе инженерных и научных расчетов MATLAB [20]. Под субсистемой здесь понимается математическая модель отдельного функционального блока, которая входит в общую модель в виде некоего макроблока. Входами субсистемы является совокупность управляющих и возмущающих воздействий для данного элемента общей модели, а выходами - переменные состояния, являющиеся предметом исследования, которые одновременно служат входными воздействиями для других субсистем. Все вычислительные операции, связанные с процессами, протекающими в рассматриваемом функциональном блоке, осуществляются внутри субсистемы. Таким образом, разработав все необходимые субсистемы общую модель системы DTC можно сформировать из готовых субсистем с минимальным использованием элементарных динамических звеньев или же вообще отказавшись от них. Изменение модели системы DTC при таком представлении сводится к замене одной или нескольких субсистем другими. Общая же структура математической модели при этом сохраняется.
До начала моделирования необходимо, прежде всего, определить те функциональные блоки, структурные схемы которых необходимо разработать до построения общей модели. Поскольку исходной при моделировании является функциональная схема системы DTC, разделение объекта исследования на отдельные функциональные блоки целесообразно проводить в соответствии с этой схемой.
В этом разделе за основу принята функциональная схема системы прямого управления моментом, приведенная на рис. 2.1.
|
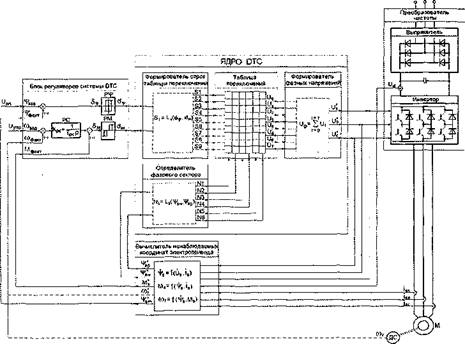
Рис. 2.1. Функциональная схема системы прямого управления моментом. Система прямого управления моментом включает в себя следующие функциональные блоки: - блок регуляторов системы DTC; - блок формирования строк таблицы переключений; - блок определения фазового сектора; - блок, реализующий таблицу переключений; - блок формирования фазных напряжений; - блок вычисления ненаблюдаемых координат электропривода. |
Эти блоки целесообразно представить в виде субсистем при формировании математической модели электропривода в целом. Для блока регуляторов системы DTC входными воздействиями являются управляющий сигнал Uynp, пропорциональный заданной частоте вращения шзад, опорный сигнал Uon, пропорциональный заданному значению модуля потокосцепления статора двигателя ¥ а также сигналы обратных связей по фактическим значениям контролируемых переменных, а именно, по модулю потокосцепления статора ¥ , по электромагнитному моменту
Мфакт и по частоте вращения двигателя шфакт. Выходными сигналами этой
субсистемы являются коммутационные функции релейных регуляторов потокосцепления статора и электромагнитного момента двигателя dY и dM, которые являются входными воздействиями для следующей субсистемы - блока формирования строк таблицы переключений. Выходными сигналами этой субсистемы являются номера строк таблицы S1...S9, количество которых определяется выбранной конфигурацией релейных регуляторов Р¥ и РМ и принятой таблицей переключений. Минимальное количество строк таблицы - 4, максимальное - 9. Поэтому на рис. 2.1 связи S5...S9 показаны пунктиром. Следующей субсистемой является блок определения фазового сектора. Входными воздействиями для этой субсистемы являются составляющие потокосцепления статора в неподвижной системе координат 'Fsa и 'Fsp. В ряде случаев удобнее использовать в качестве входных сигналов для этой субсистемы не составляющие вектора потокосцепления статора, а тригонометрические функции угла 'Fs (sin|/s и cosj/s), о чем было сказано выше. Выходными сигналами этой субсистемы являются номера столбцов таблицы переключений N1 ...N6. Выходные сигналы формирователя строк таблицы переключений и определителя фазового сектора представляют собой входные управляющие воздействия для следующей субсистемы, реализующей таблицу переключений. Выходными сигналами таблицы являются восемь возможных пространственных состояний результирующего вектора выходного напряжения преобразователя частоты U0...U7. Эти сигналы являются входными воздействиями для субсистемы, в которой воспроизводится блок формирования фазных напряжений. Выходные сигналы формирователя фазных напряжений UA*, UB* и Uc* представляют собой алгоритм переключения электронных ключей силового инвертора преобразователя частоты. Они же служат входными воздействиями для последней субсистемы - блока вычисления ненаблюдаемых координат электропривода. Формирователь строк таблицы переключений, определитель фазового сектора, таблица переключений и формирователь фазных напряжений образуют так называемое ядро DTC. Помимо сигналов UA*, UB* и Uc*, входными воздействиями для вычислителя ненаблюдаемых координат являются сигнал с выхода датчика напряжения в звене постоянного тока преобразователя частоты Ud и сигналы с датчиков фазных токов в статорной цепи электродвигателя iSA, iSB и isc. На выходе этой субсистемы получаются сигналы, пропорциональные составляющим вектора потокосцепления статора в системе координат (а - (3) - и модулю потокосцепления статора ^sm, электромагнитному моменту М*э и частоте вращения ротора двигателя со*г. Здесь и далее символом (*) обозначены вычисленные значения переменных. Составляющие вектора потокосцепления статора 'I'*sa и служат входными воздействиями для определителя фазового сектора. Остальные сигналы 0^*^, М*э и со*г) используются в качестве сигналов обратных связей для блока регуляторов системы DTC. Если сигналы обратных связей по модулю вектора потокосцепления статора и по электромагнитному моменту двигателя - всегда вычисленные, то сигнал обратной связи по частоте вращения двигателя может быть как вычисленным (со*г), так и полученным путем прямой индикации с помощью вращающегося датчика скорости ДС (wr). Поэтому на рис. 2.1 эти две связи, исключающие друг друга, показаны пунктиром.