Зависимость рекомбинации от температуры и легирования
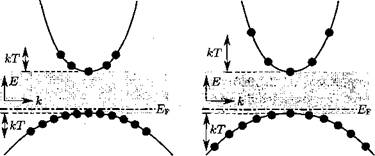
Зависимость вероятности рекомбинации от температуры представлена на рис. 3.2, который показывает параболическую зависимость Е(к) при низких и высоких температурах. При ее анализе можно выявить уменьшение числа носителей в интервале значений квазиимпульса dk с увеличением температуры. Так как при излучательной рекомбинации выполняется закон сохранения квазиимпульса и вероятность рекомбинации электронов пропорциональна количеству свободных дырок с равным значением квазиимпульса, вероятность рекомбинации уменьшается с ростом температуры. Этот факт подтверждается соотношениями (3.24) и (3.25), которые показывают, что коэффициент бимолекулярной рекомбинации зависит от температуры обратно пропорционально Тъ'2.
О Библиографию со ссылками на цикл оригинальных работ Д. 3. Гарбузова с соавторами см. в [5].
|
|
|
а |
|
б |
|
Рис. 3.2. Распределение носителей заряда при низкой (а) и высокой (б) температуре. Вероятность рекомбинации уменьшается при высокой температуре из-за сокращения числа носителей в интервале значений квазиимпульса dk |
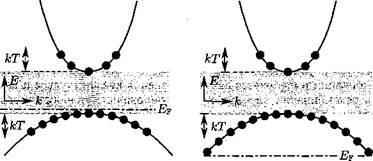
Зависимость вероятности рекомбинации от концентрации легирующих примесей представлена на рис. 3.3, на котором показаны функции Е(к) в случае невырожденного и вырожденного легирования. Из них следует, что число дырок в интервале значений квазиимпульса dk остается постоянным в вырожденном случае. Поэтому в вырожденном полупроводнике вероятность рекомбинации не увеличивается.
Это подтверждается квантово-механическим расчетом коэффициента бимолекулярной рекомбинации, зависимость которого от концентрации дырок представлена на рис. 3.4 (Waldron, 2002). Их него следует, что коэффициент бимолекулярной рекомбинации в случае вырожденного легирования насыщается. Модель Ван Росбрука-Шокли такой
а б
|
Рис. 3.3. Распределение носителей заряда в случае невырожденного (а) и вырожденного (б) полупроводника p-типа. В случае вырожденного легирования перекрытие между электронами и дырками с одинаковыми значениями квазиимпульса не увеличивается |
зависимости не предсказывает, так как ее применение ограничено невырожденным случаем.
Уравнение (3.22) справедливо в случае невырожденных полупроводников, для которых характерна сравнительно малая концентрация носителей. Следовательно, и уравнения для расчета коэффициентов бимолекулярной рекомбинации также применимы только для невырожденных полупроводников. В этом случае коэффициент В не зависит от концентрации носителей. Однако при очень высоких концентрациях носителей величина коэффициента В уменьшается, что связано с увеличением рассогласования между квазиимпульсами электронов и дырок. Поэтому для вырожденных полупроводников справедливо выражение D = В — (n/Nc) ■ В*, которое показывает, что с ростом концентрации носителей коэффициент рекомбинации падает. Более подробное описание поведения коэффициента рекомбинации при высоких концентрациях носителей, а также численные значения величины В* можно найти в работах (Agrawal, Dutta, 1986; Olshansky, 1984) 0.
Упражнение. Определение эффективности излучательной рекомбинации
На основе анализа температурных зависимостей скоростей излучательной и безызлучательной рекомбинации по моделям Ван Росбрука-Шокли и Шокли-Рида предскажите температурную зависимость эффективности излучательной рекомбинации в различных полупроводниках.