ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ПОЛЯ НАПРЯЖЕНИЙ ЛИНЕЙНОЙ МЕХАНИКИ ТРЕЩИН
3.2.1.
три вида Трещин
И СИНГУЛЯРНЫЕ ПОЛЯ НАПРЯЖЕНИЙ
С трещинами связано 4 аварийных фактора из табл. 1.3 и почти 12% всех случаев разрушения конструкций.
Сравнительно новая, возникшая в 1950-х годах наука «Механика разрушения» занимается исследованием полей напряжений и деформаций у вершины трещины и критериями разрушения материала под действием этих полей.
|
|
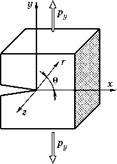
На рис. 3.30 показаны три базовых случая нагружения детали с трещиной. Локальные декартовы координаты (x, y, z) имеют начало в вершине трещины. Кроме того, используются цилиндрические координаты (г, 0, z), показанные на схеме рис. 3.30. Ось х и направление 0 = 0 располагаются в плоскости трещины.
|
|
|
II |
|
пі |
|
Рис. 3.30 Три вида трещин механики разрушения: I — нормального отрыва, II — поперечного сдвига, III — продольного сдвига. |
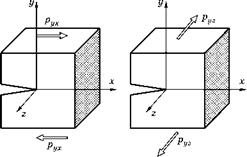
Вдали от трещины материал нагружен равномерно распределенными напряжениями:
■ ру — в случае трещины нормального отрыва (тип I);
■ Рух — в случае трещины поперечного сдвига (тип II);
■ Руг — в случае трещины продольного сдвига (тип III).
Общий случай произвольного нагружения тела с трещиной
можно получить, суммируя поля напряжений этих трех задач. Распределение напряжений у вершины трещины в общем случае можно представить в виде степенных рядов от радиус-вектора г, умноженного на некоторую функцию от угла 0. Но только первые члены этих степенных рядов являются сингулярными. Они неограниченно возрастают при приближении к вершине трещины. Все остальные члены ряда у корня трещины малы по сравнению с первыми. Если при анализе поля напряжений у вершины трещины ограничиться учетом только этих сингулярных членов, то формулы для вычисления напряжений приобретают очень простой вид.
°ij =^К=Т'f j’ N(0), (3.60)
где индексом N обозначен вид трещины (I, II, III), а индексы i и j могут принимать значения цилиндрических координат г, 0 и г. Эти поля напряжений проще всего вычисляются в цилиндрических координатах (г, 0, г).
Постоянная KN, пропорциональная внешней нагрузке, называется коэффициентом интенсивности напряжений. Коэффициент концентрации напряжений в этом случае не имеет смысла, так как напряжения по формуле (3.60) при радиусе г, стремящемся к нулю, устремляются к бесконечности. Но при этом уровень эпюры напряжений задается коэффициентом интенсивности напряжений.
В случае сквозной трещины в бесконечной пластине формулы для вычисления коэффициентов интенсивности напряжений очень просты:
KI — pxx "Jft' 1;
KII - pxy 'Vя' l; (3.61)
KIII - рхг 1Л'1,
где l — полудлина трещины.
В плоскости 0 = 0 (или у = 0; г = х) на продолжении трещины абсолютные значения функций от угла f j, N(0) принимают значения 1 или 0. Поэтому в этой плоскости (по которой обычно рас-
пространяется трещина) наиболее значимые напряжения описываются формулой v
KN___
(3.62)
Если значения KN из формулы (3.61) подставить в формулу
(3.62) и во всех случаях нагрузку обозначить черезр, то получится достаточно общее выражение для вычисления наибольших напряжений в опасном сечении детали с трещиной:
1
|
(3.63) |
— - Р V2 • (х/I)'
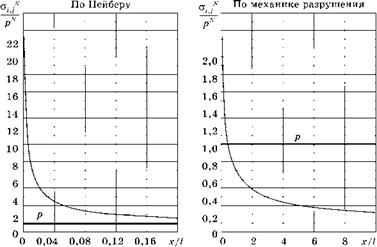
Имеет смысл оценить эту зависимость количественно, она построена на рис. 3.31.
Из рис. 3.31 видно, что поля напряжений, вычисляемые по формуле (3.63), характеризуются следующими особенностями:
■ напряжения устремляются к бесконечности при х ^ 0;
■ уже на расстоянии х = 0,5 от характерного размера трещины l напряжения приближаются к номинальным приложенным к пластине напряжениям р;
■ на больших расстояниях от вершины трещины вычисленные по формуле (3.63) механики разрушения напряжения меньше приложенных к детали, и с увеличением этого расстояния стремятся к нулю, что не соответствует действительности.
|
Рис. 3.31 Общий график распределения наибольших напряжений в опасном сечении у трещины |
Теперь обратимся к функциям от угла 0, на которые нужно умножить масштаб напряжений на графиках рис. 3.31, чтобы получить распределение напряжений в любой плоскости, наклоненной к оси х под углом 0.
Трещина нормального отрыва (N = I) похожа на непровар в поперечном стыковом шве, для нее функции f;, j, N(0) формул (3.60) имеют вид:
|
fln(I) - 3cos (£) + Icos ( 3 ); |
fmW - 4cos (I)-4cos (f); fcos (|) + icos (f
(3.64)
fm(I) - 4Sin(I) + 4Sin(f).
Функция frr1(0) необходима для вычисления arr в задаче I, функция feei(0) — для вычисления стее в этой задаче, frt1(0) — для вычисления тг0. Естественно, что в случае плоского напряженного состояния стг = 0; а в случае плоской деформации єг = 0 и стг = v - (ax + ay). Все остальные напряжения равны нулю.
Так как при вычислении любых напряжений множитель KN/ (I - л - r)1/2 выносится за скобки, можно записать следующие выражения для функций от угла:
для вычисления напряжений агг при плоской деформации:
fzz(0) = v [frr(0)+ fee(0)]; (3.65)
для вычисления интенсивности напряжений а; по формуле (2.22):
f (0) = ^[frr (Є) - fee (Є)]2 + [f99 (Є) - fzz (Є)]2 + f (Є) - frr (Є)]2 + 6 ■ f2 (Є) , (3.66)
для вычисления главных нормальных напряжений ст1 по формуле (2.17) получим
f /m frr (Є) + fee (Є) Ч[frr (Є) - fee (Є)]2 + 4 • fr2 (0)
71(e) - 2 , (3.67)
для вычисления жесткости напряженного состояния Ц = СТ1/СТ;:
f (0) = Щ. (3.68)
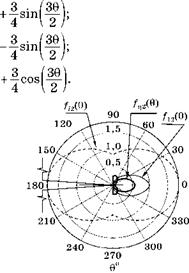
На рис. 3.32 приведены вычисленные по этим формулам графики. Следует обратить внимание на кривую для f;1(0), которая очерчивает радиус пластической зоны у вершины трещины при различных углах 0. При 0 = 0 отношение напряжений: а = а2/ Ст1 = 1; ц = 2,5.
|
Рис. 3.32 Эпюры функций /(0) для трещины нормального отрыва (I) |
В практических расчетах условий разрушения главным образом используются поля напряжений для трещин нормального отрыва и коэффициент интенсивности напряжений KI.
Трещина поперечного сдвига (II) похожа на непровар в корне лобового шва.
|
Irr 2(I) = - |sin (I) /ее2(е)=- fsin (f |
|
rif(I) = + Tc°s (Є |
|
(3.69) |
|
Рис. 3.33 Полярные диаграммы для функций от угла трещины поперечного сдвига |
|
|
|
Ir |
|
Так как физический смысл графиков функций (3.69) воспринимается трудно, на рис. 3.33 по формулам (3.66)- (3.68) с помощью формул (3.69) построены полярные диаграммы для функций главных нормальных напряжений /12, интенсивности напряжений /і2 и жесткости напряженного состояния /п2 для трещины типа II. Из графика видно, что максимальная жесткость напряженного состояния очень мала (не превышает 0,6). Максимальное значение функции главного напряжения ст1 равно 1,0. |
Для трещин поперечного сдвига функции от угла имеют следующий вид:
|
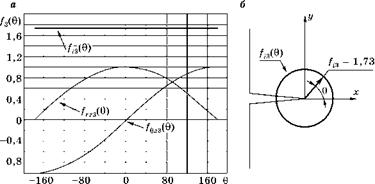
Рис. 3.34 Функции от угла для трещины продольного сдвига (III) |
Но велико значение функции для интенсивности напряжений ст;. В направлении плоскости трещины (0 = 0) оно равно V3.
Наконец, трещины продольного сдвига (III) похожи на не- провар в корне фланговых швов. Для них существуют только два касательных напряжения xrz и т0г. Остальные напряжения равны нулю. Функции от угла 0 в этом случае имеют совсем простой вид:
|
(3.70) |
/„а(Є) = sin j 2);
/гЄ3(0) = cos j 2).
Вычисленные по этим формулам графики представлены на рис. 3.34.
Видно, что в этом случае функция для стг не зависит от угла 0:
|
=V3. |
Ыб) = ^ лІ02 + 02 + 02 + 6 • [(/rz3(6))2 + f з (Є))2 + 02] =
sin — + cos^ —
Поэтому для таких трещин пластическая зона у вершины имеет круглую форму, как показано на правом рисунке. Радиус круга: fi3(0) = 31/2 = 1,73. Это же значение функции интенсивности напряжений было отмечено для трещины поперечного сдвига в направлении плоскости трещины.