МИКРО ПЛАЗМЕННАЯ СВАРКА

ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ СЖАТОЙ ДУГИ НИЗКОГО ДАВЛЕНИЯ

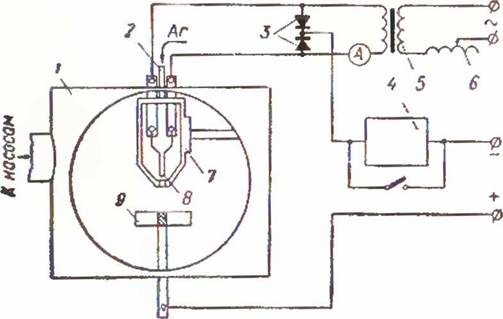
Разработанный в ИЭС им. Е. О. Патопа способ сварки сжатой дугой в вакууме [16] нашел применение при изготовлении свар­ных конструкций из химически активных металлов и сплавов, узлов электронных и электровакуумных приборов, требующих высококачественной защиты, а также при других видах терми­ческой обработки металлов. Сущность этого способа состоит в том, что в вакуумной камере размещается плазменная горелка, внутрь которой подается газ, истекающий через сопло в каме­ру. Из камеры газ непрерывно откачивается вакуумным насо­сом. Дуга горит между катодом плазмотрона и изделием — анодом, размещенным внутри камеры (рис. 7).

Вычисление параметров такой дуги связано со значитель­ными трудностями, поскольку отсутствуют методы ее расчета. Единственный параметр, поддающийся оценке,— средняя плот­ность тока в каьале плазмотрона. Для решения технологиче­ских задач важно знать плотность тока не в плазмотроне, а на изделии и уметь управлять ею.

Рассмотрим механизм сжатия дуги низкого давления вне плазмотрона, вычислим функцию радиального распределения плоіьости тока в столбе и установим количественные связи па­раметров дуги с режимом ее горения.

По мере уменьшения давления в ка-мере, при котором горит дуга, увеличивается отношение направленной скорости электро­нов к тепловой скорости. Если это отношение больше единицы, то ускоряющее действие электрического поля уже не может быть компенсировано силой динамического трения. Движение элек­тронов в этом случае сдерживается в основном их инерцией. Поскольку последняя очень мала, то электропроводность такой плазмы существенно увеличивается. Такая плазма становится подобной низковольтному пучку электронов. При этом роль по­ложительных ионов сводился к нейтрализации объемного заряда электронов. В работах Л. Лидски [17] ц В. М. Ямпольского tІ8] отмечаемся, что плазма низкого давления с натеканием газа через трубчатый катод представляет собой именно такой сильноточный низковольтный электронный пучок* В этой свя­зи можно предположить, что и в данном случае за срезом сопла плазмотрона также формируется квазинейтральный электрон­ный пучок. Механизм сжатия этого пучка вне плазмотрона, по нашему мнению, состоит в следующем.

Электроны плазмы под действием продольного электриче­ского поля ускоряются к аноду, а за счет поперечных состав­ляющих тепловых скоростей смещаются в радиальном направ­лении, что приводит к расширению плазмы. Перемещение элек-

Рис. 7.

Схема установки для сварки при пониженном давлении:

I — вакуумная камера; 2 — ввод плазмообразующего газа;

3 — диодная развязка;

4 — коммутатор тока;

б — накальный трансформатор;

6 — автотрансформатор;

7 — плазменная горелка;

8 — накаливаемый катод;

9 — разрезной анод.

тронов в радиальном направлении происходит перпендикулярно собственному магнитному полю, создаваемому током дуги. В результате взаимодействия радиальной составляющей ско­рости электрона с собственным магнитным полем изменяется характер их движения. Электроны (при низком давлении начи­нают вращаться вокруг силовой линии магнитного поля. Когда частота их вращения бильше частоты их соударен-ий в плазме, магнитное поле задерживает диффузию электронов в радиаль­ном направлении. В этом случае тепловая скорость движения ионов поперек столба становится больше скорости электронов вследствие большего радиуса кривизны траектории иона в маг­нитном поле. Различие в скоростях ионов и электронов в попе­речном направлении порождает электрическое поле, которое тормозит ионы и ускоряет электроны так, что их движение поперек столба дуги происходит с одинаковой амбиполярной скоростью. Таким образом, электроны, движущиеся в направлен нии к аноду, под действием поперечных составляющих тепловых скоростей ионов вместе с ними смещаются в радиальном на­правлении. В результате плазма расширяется, плотность тока в столбе уменылаегся. Расширение плазмы тем меньше, чем больше направленная скорость электронов и ниже темпераїура ионов.

С учетом максвелловского закона распределения попереч­ных составляющих тепловых скоростей для изложенного в ра­боте [19] механизма сжатия столба дуги низкого давления нами получено выражение, описывающее радиальное распределение плотности тока:

/ (г) = /о [ 1 + 9Т^Гг) ехр (— air2). (1.11)

г “T - а2гс J

Здесь /о — плотность тока на оси столба, которая выражается через среднюю плотность /с в канале плазмотрона как

/о = /с [1 — ехр (— а|г£)], (Ї-12)

где al — параметр, имеющий вполне определенный физический смысл и служащий мерой сосредоточенности тока в столбе дуги

2 Mi (ueY

низкого давления, а2 = 2ИгТ/ * ^1я ^ — соответственно масса

и температура ионов; ft-—постоянная Больцмана; — направ­ленная скорость электронов, создаваемая электрическим полем; z — координата вдоль оси столба, отсчитываемая от среза сопла плазмотрона.

Из формулы (L12) следует, что при О плотность тока на оси столба /0 стремится к плотности тока /с в канале сопла плазмотрона* Из выражения для а* следует, что чем больше
масса и ниже температура ионов, а также больше направлен­ная скорость электронов, тем сильнее сжимается дуга. Из этой же формулы видно, чіо степень сосредоточенности тока зави­сит от длины дуги. Чем длиннее дуга, тем меньше плотность тока на изделии.

Используя формулу (1.11), можно легко установить связь между током дуги /д, плотностью тока /о, радиусом сопла гс и параметром ар

оА

/д = 2* Г / (г) rdr = (1.13)

J ао

О

где

2 2 * "Г а2Гс

С°”Й2о/. і „2~2

и имеет смысл коэффициента сосредоточенности тока.

Легко показать, что равенству /да2о=л/о соответствует рас­пределение плотности тока/(а), которое, как и в дуге при атмос­ферном давлении, оп-исывается той же формулой (1*8), но с другим значением коэффициента сосредоточенности и*.

Теперь имеет смысл проанализировать функциональную за­висимость коэффициента о от основных параметров плазмы.

Для этого необходимо определить направленную скорость элек­тронов иЕ, которая, как легко понять, зависит от напряжен­ности электрического поля и осевого градиента электронного давления. Этот градиент, как и электрическое поле, ускоряет электроны в направлении к аноду и вносит заметный вклад в направленную скорость иЕ электронов.

г. о d [ аО

Поэтому действие градиента ^ Iр

|ре = р и электрического поля Е на скорость электронов

можно заменить действием эквивалентного электрического поля Ее:

е‘~в-^т-І"'{рхТ-Л)- <ІІ4>

Здесь е и Те — заряд и температура электронов; а — степень

пе

ионизации, а = —-—; 0 — коэффициент, учитывающий неизо-

О ^ t'

т

термичность плазмы, 6 — р — суммарное давление, р = ра + - г ре + Pi-

d Г ^

Существование градиента р ионного давления, нао­

борот, уменьшает направленную скорость ионов. Поэтому экви­валентное поле Ei для ионов имеет ьид

£'-£+т7''1'"('’пЫ - <U5>

Для случая, когда Ei^z О, из выражений (1.14) и (1.15) имеем

Ее — Е (1 + 6) —jTe (1.16)

Выполняя математические преобразования для направленной

скорости электронов (ue ~ ^Ее), характерной для плазмы низ­кого давления [20], с учетом выражения (1-16) находим

а| = 2,73- ю—»8(1+i;0)>A/1 |е(1 +е) — 8,625- 10-5Гв^1пОІ

pZ <Sy L J

(I.17)

где A — атомный вес газа; Ss = + a (s*i— sea) — сечение упру­

гого соударения электронов в плазме.

Вычисления показывают, что для реальных значений пара­метров плазмы: в — 5; а —0,15; р = 30 Н/м2^0,225 мм рт. ст.;

z = 0,02 м, Ss = 4 * 10““19 м2; Е = 33 В/м; А = 40; ~ = 0 коэф­фициент al — 1,25 • 106 м~~ = 1,25 мм”2.

Для тока дуги /Д=90А, радиуса сопла гс— 0,6 мм и на­йденного значения а2 по уравнению (1.12) определяем, что /0~

^ 28,7 А/мм2. При напряженности поля £=25 В/м плотность тока /с~22,9 А/мм2. Эти значения находятся в хорошем соот­ветствии с экспериментальными данными [21].

Из формулы (1.17) видно, что в зависимости от распределе­ния давления p(z) в разрядном промежутке столб дуги может иметь различную форму. Если произведение z2p(z) — функция растущая, го при постоянных остальных параметрах коэффи­циент а2 (г) есть функция падающая. Поэтому в направлении к

аноду дуга будет расширяться. Если же произведение z2p(z)~ ~ const, то дуга приобретает цилиндрическую форму; коэффи­циент а22 перестает зависеть от г и в любом поперечном сече­нии столба устанавливается одинаковая плотность тока.

В силу того что /о<7с> по отношению к радиусу канала соп­ла столб дуги вблизи него в любом случае будет расширяться. При удалении от сопла к аноду форма столба, как отмечалось, определяется в основном произведением z2p(z).

Коэффициент сосредоточенности тока дуги низкого давления также зависит от рода плазмообразующего газа: чем выше

атомный вес газа, тем сильнее сжимается дуга. В гелии, масса которого в десять раз меньше маесы аргона, дуга низкого дав­ления будет сжиматься значительно слабее, чем в аргоне. Практически технологические параметры дуги низкого давления регулируются величиной тока, радиусом канала сипла плазмо­трона и натеканием плазмообразующего газа.