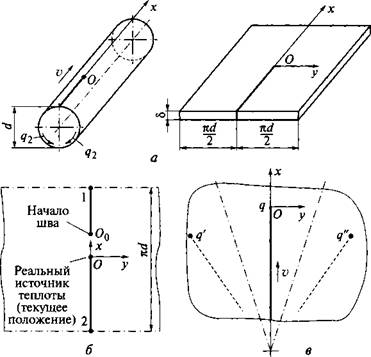
Нагрев тонкостенных оболочек
При однопроходной сварке продольных и кольцевых швов тонкостенных оболочек, имеющих цилиндрическую или конусную форму, их нагрев (несмотря на кривизну) можно рассматривать как случай нагрева пластины линейным источником теплоты. Это объясняется тем, что цилиндр и конус являются развертывающимися поверхностями, а при однопроходной сварке с полным проплавлением температуру по толщине листа можно считать выравненной. На распространение теплоты могут оказывать влияние лишь размеры заготовки.
При сварке продольного шва тонкостенной трубы или обечайки малого диаметра имеет место встреча тепловых потоков в сечении, диаметрально противоположном стыку (рис. 6.19, а). Поскольку тепловые потоки, подводимые к этому сечению справа и слева, одинаковы, то это сечение можно рассматривать как адиабатическую границу, а данный случай - как сварку двух узких пластин встык.
|
Рис. 6.19. Схемы движения источников при нагреве тонкостенных оболочек: а - сварка продольного стыка трубы; (слева - общий вид, справа - развертка); б - сварка кольцевого стыка; в - сварка по образующей конуса |
При сварке кольцевого стыка труб малого диаметра, когда время сварки невелико, температура точек, лежащих вблизи места начала сварки, к моменту замыкания кольцевого шва оказывается достаточно высокой (автоподогрев). Для учета этого явления при расчете температур можно использовать схему бесконечной пластины с двумя подвижными линейными источниками, движущимися синхронно в одном направлении вдоль оси шва (рис. 6.19, б). Источник 1 удаляется от точки Oq начала шва, а источник 2 приближается к ней; расстояние между источниками остается неизменным, равным периметру трубы nd. Поскольку время сварки невелико, следует учитывать процесс теплонасыщения для температурного поля каждого источника (см. разд. 6.8). Результирующее температурное поле во время сварки определяется наложением температурных полей двух источников. После выхода источника 2 в точку <9о и прекращения сварки обе составляющие температуры определяются в стадии выравнивания (см. разд. 6.8).
При выполнении сварки вдоль образующей тонкостенного конуса небольшого диаметра температурное поле может быть определено путем разворачивания конуса в клиновидную пластину с осью симметрии, совпадающей с осью шва. Две адиабатические границы на краях клиновидной пластины учитываем введением в расчет двух фиктивных источников q' и q' движущихся, как и реальный источник, в радиальном направлении (рис. 6.19, в).
Распространение теплоты при сварке экваториальных однопроходных швов на тонкостенных сферах происходит при некотором стеснении теплового потока вследствие кривизны сферической оболочки в двух направлениях. Температура точек оказывается несколько выше, чем в бесконечной пластине той же толщины. На сферах большого диаметра влиянием кривизны можно пренебречь, если выполняется соотношение
<200, (6.42)
vcpbR,
где v - скорость сварки; 8 - толщина стенки сферы; Rc - радиус сферы.
В ряде случаев сварка тонкостенных труб выполняется за несколько проходов без остановки процесса. Приближенный расчет температур можно провести, используя схему бесконечной пластины с несколькими последовательно движущимися друг за другом источниками (как это было сделано для случая сварки кольцевого шва трубы малого диаметра). В зависимости от режима сварки можно использовать схемы подвижных или быстродвижущихся источников.