Быстродвижущийся точечный источник на поверхности полубесконечного тела
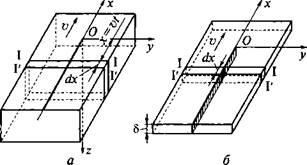
Рассмотрим тонкий поперечный слой толщиной dx, расположенный в полубесконечном теле перпендикулярно направлению движения источника теплоты (рис. 6.17, а). Быстродвижущийся точечный источник теплоты мощностью q выделяет на участке dx за время dt = dx/v количество теплоты Q = qdt = qdx/v. Эта теплота распространяется только в плоскости выделенного слоя, который
|
Рис. 6.17. Схемы выделения зон распространения теплоты от быстродвижущихся источников: а - точечный источник на поверхности полубесконечного тела; б - линейный источник в бесконечной пластине |
можно считать полубесконечной пластиной толщиной 5 = dx без теплоотдачи с поверхности; в пластине действует мгновенный линейный источник теплоты Q (тепловыми потоками в направлении оси Ох пренебрегаем, так как источник теплоты быстродвижущийся). Для описания температурного поля используем готовое решение (6.2). С учетом адиабатической границы запишем следующее выражение для нестационарного температурного поля в рассматриваемом слое:
|
20/5 |
|
Ф_ 2я Xt |
|
г 4 at |
|
г 4 at |
|
Т(г, 0 = гн+- |
|
= Ти + |
|
(6.37) |
|
г exp |
|
exp |
|
ср] (4 nat)‘ |
Г2 2
где г = ]у +z - расстояние от направления движения источника теплоты (оси Ох) до рассматриваемой точки; t - время, отсчи-
тываемое от момента прохождения источника через сечение, в котором находится рассматриваемая точка.
Таким образом, процесс распространения теплоты в массивном теле от быстродвижущегося точечного источника можно представить совокупностью одинаковых сдвинутых во времени, не взаимодействующих между собой элементарных плоских процессов распространения теплоты в поперечных сечениях от мгновенных источников. Поэтому для получения выражения, описывающего температурное поле в подвижной системе координат, не требуется выполнять интегрирование, достаточно лишь выразить время распространения теплоты в каждом сечении через его координату л: и скорость движения источника V, т. е.
( = (6.38)
V
Подставив соотношение (6.38) в выражение (6.37), получим
(6.39)
|
4ах |
Т(г, х) = Тн - ———ехр 2пкх
Следует отметить, что выражение (6.39) применимо только для области, находящейся позади источника теплоты, т. е. при л: < 0. Температуры всех точек тела, расположенных перед источником,
равны начальной температуре Гн.
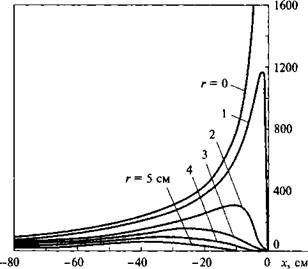
Распределение температур (рис. 6.18), описываемое выражением (6.39), в области остывания незначительно отличается от распределения, описываемого выражением (6.24) для схемы подвижного источника, которое справедливо при любой скорости движения источника теплоты. На оси Ох позади источника распределения температур, рассчитанные по выражениям (6.24) и
(6.39) , полностью совпадают. Это несложно показать, учитывая, что координаты у и z точек, лежащих на оси Ох, равны нулю; при этом показатель экспоненты в обоих выражениях тоже равен нулю (г = 0; R = - х). Таким образом, в подвижной системе координат распределение температур на оси Ох позади точечного источника постоянной мощности, движущегося равномерно и прямолинейно по поверхности полубесконечного тела, не зависит от скорости его движения:
Т(0, х) - Гн ~~т~- (6-40)
2лах
В данном случае распределение температур позади источника подчиняется гиперболическому закону, а длина «хвостовой» части любой изотермы однозначно определяется мощностью источника и коэффициентом теплопроводности материала.
|
a |
|
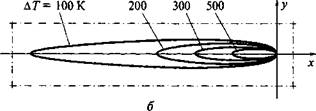
Рис. 6.18. Квазистационарное температурное поле быстродвижущегося точечного источника, действующего на поверхности полубесконечного тела: а - распределение приращений температур по линиям, параллельным направлению движения источника (оси Ох) б - изотермы на поверхности тела |