Периоды теплонасыщения и выравнивания температур
В начальный период действия источника теплоты (например, после зажигания дуги) температуры точек тела монотонно возрастают от начальных значений до температур предельного (стационарного или квазистационарного) состояния, которое теоретически устанавливается в течение бесконечно большого промежутка времени. В действительности длительность этого периода конечна, и он носит название периода теплонасыщения. Расчет температур, которые в этот период для различных расчетных схем определяются выражениями (6.19), (6.21) и (6.23), можно выполнять численными методами на ЭВМ либо аналитическими - по формулам предельного состояния для принятой расчетной схемы, но с обязательным учетом поправочного коэффициента теплонасыщения
Т-Т
Jnp
где T(t) - температура на стадии теплонасыщения; t - время от момента начала сварки; 7^ - начальная температура; Гпр - температура предельного состояния.
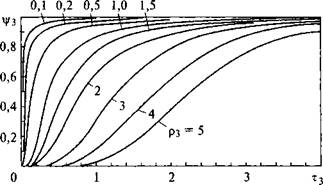
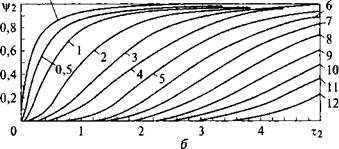
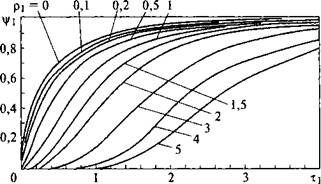
Коэффициент теплонасыщения 4у возрастает от нуля в начальный момент времени до единицы в предельном состоянии. Значения коэффициента теплонасыщения для трех основных расчетных схем процесса распространения теплоты определяется по номограммам (рис. 6.15) в зависимости от безразмерных критериев расстояния (pi, р2, рз) и времени (tj, 12, тз). Индекс при указанных критериях соответствует размерности соответствующего процесса (/ - линейный, 2 - плоский, 3 - пространственный).
Для пространственного процесса распространения теплоты (схемы бесконечного тела, полубесконечного тела и плоского слоя)
безразмерные критерии рз и тз вычисляют по формулам
vR v2t
<б'зі)
Для плоского процесса распространения теплоты (схема пластины) безразмерные критерии р2 и тг вычисляют по формулам
|
Г 2 V, — + Ъ v 4а ч у |
|
(6.32) |
Р2 = г
V 4 а2 а
где Ъ - коэффициент температуроотдачи пластины.
|
|
а
|
Р2 “ 0,2
|
|
|
|
Рис. 6.15. Номограммы для определения коэффициента теплонасыщения: Уз - для схемы точечного источника в массивном теле (л); у2 - Для схемы линейного источника в бесконечной пластине (б); у і - для схемы плоского источника в стержне (в) |
|
в |
Для линейного процесса распространения теплоты (схема стержня) безразмерные критерии pi и х вычисляют по формулам:
|
|
|
V |
|
/ |
(6.33)
где Ъ - коэффициент температуроотдачи стержня.
Из номограмм (см. рис. 6.15) следует, что чем больше значение безразмерного критерия расстояния р, тем позже достигается предельное состояние процесса. Чем более стеснен поток теплоты, тем медленнее идет процесс теплонасыщения.
|
(6.34) |
Следует иметь в виду, что расстояние от источника теплоты до точки тела (R, г или х), входящее в формулы (6.31)—(6.33), определяется в подвижной системе координат с учетом заданных координат точки и времени t, прошедшего после начала сварки, т. е.
x = xQ-vt; у = Уо', z = z0.
Здесь х9 у, z — координаты точки в подвижной системе координат, связанной с источником; jco, уо, zq - координаты точки в неподвижной системе координат.
После прекращения действия источника теплоты наступает период выравнивания температур. Введенная ранее теплота продолжает распространяться в теле и отводиться в окружающую
|
У
|
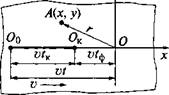
среду. Расчет температур в этот период выполняют с помощью приема, предусматривающего ввод в расчетную схему фиктивного источника и совмещенного с ним фиктивного стока той же мощности, компенсирующего действие фиктивного источника (рис. 6.16). Благодаря этому
Рис. 6.16. Схема действия задача о прекращении действия ис-
фиктивных источника и стока точника превращается в задачу о
в период выравнивания тем - начале действия стока, которую ре - ператур
г шают с использованием изложенных
выше подходов для периода теплонасыщения. Температура после окончания сварки может быть рассчитана по формуле
по=ти+(Тпр - тиmo - w - o)i
|
(6.35) |
где T(t) - температура на стадии выравнивания температур; Гпр - температура предельного состояния; ¥(0 - коэффициент теплона - сыщения, соответствующий длительности нагрева t - /к) - коэффициент теплонасьнцения, соответствующий длительности работы стока теплоты t - tK> t - время от момента начала сварки; tK - время окончания сварки (время действия источника).
В тех случаях, когда время действия реального источника достаточно велико и можно полагать, что к моменту прекращения нагрева было достигнуто предельное состояние (Ч^/) = 1), расчетное выражение (6.35) упрощается:
т = тн + (Гпр - Гн)[ і - ЧЧ* - 'к)]. (6.36)