Понятие о сварочных деформациях и напряжениях
При равномерном нагреве материала происходит его свободное расширение без возникновения напряжений. Если же осуществляется неравномерный нагрев тела, то связи нагретых участков с ненагретыми препятствуют свободному расширению тела. Вследствие этого в теле возникают температурные собственные
напряжения, существующие при отсутствии приложенных к нему внешних сил. Температурные напряжения, возникающие в процессе сварки, принято называть временными напряжениями. Временные напряжения существуют в теле в процессе сварки на всех стадиях нагрева, выравнивания температур и охлаждения.
Неравномерный нагрев и изменение объема металла вследствие температурного расширения, фазовых или структурных превращений приводят к возникновению упругих и пластических деформаций. В результате пластических деформаций в сварных элементах после полного охлаждения остаются собственные напряжения, которые называются остаточными напряжениями.
|
|
|
5) |
|
|
|
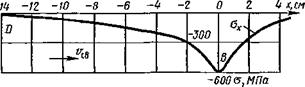
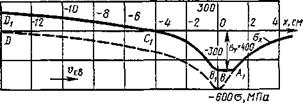
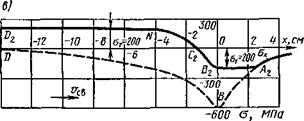
Рис. 11.1. Механизм образования продольных напряжений Ох в процессе нагрева кромки пластины движущимся источником теплоты при различных значениях предела текучести металла: а — оо, б — ст — 400 МПа, в — сгт= 200 МПа |
Механизм образования остаточных напряжений при сварке можно проиллюстрировать следующим примером [17]. Рассмотрим пластину, по краю которой перемещается источник нагрева, создающий установившееся температурное поле с максимальным нагревом в точке расположения источника (точка О на рис. 11.1, а). При этом в крайнем волокне пластины возникает/
ют сжимающие продольные напряжения <зх, распределение которых показано на рис. 11.1, а. Если максимальные значения напряжений Ох не достигают предела текучести металла, то это означает, что при нагреве в нем происходят только упругие деформации. Следовательно, после полного остывания напряжения окажутся равными нулю, т. е. остаточные напряжения в этом случае отсутствуют (рис. 11.1, а).
Рассмотрим этот же случай нагрева в предположении, что предел текучести металла составляет <гт == 400 МПа и не изменяется в процессе нагрева. Тогда напряжения <т* первоначально возрастают, достигая значения предела текучести в точке А (рис. 11.1,6). На участке АВ происходит пластическая деформация укорочения, а напряжения будут равны пределу текучести о* = <гт = 400 МПа, если не учитывать упрочнения металла. Начиная с точки В, сжимающие напряжения уменьшаются по кривой BCDi, которая эквидистантна кривой BD, перенесенной с рис. 11.1, с. В точке С і напряжения равны нулю, а далее переходят в растягивающие. После полного остывания (точка Dі) сохраняются остаточные растягивающие напряжения о0СТ, значения которых в данном случае меньше предела текучести металла.
Далее рассмотрим этот же случай нагрева в предположении, что предел текучести имеет меньшее значение, например 0Т=2ОО МПа (рис. 11.1, е). Напряжения сжатия <тх достигают в точке Аг значения предела текучести, и на участке Л2В2 будет происходить пластическая деформация укорочения. Затем напряжения сжатия уменьшаются, в точке Сг окажутся равными нулю и далее переходят в растягивающие. В точке N растягивающие напряжения достигают предела текучести и на участке ND2 происходят пластические деформации удлинения. После полного остывания пластины (точка Пг) сохраняются остаточные собственные растягивающие напряжения, равные пределу текучести металла о,-=200 МПа.
Собственные напряжения, как временные, так и остаточные, подразделяют в зависимости от объема их взаимного уравновешивания на напряжения первого рода, уравновешенные в макрообъемах; напряжения второго рода, уравновешенные в объемах одного или нескольких зерен; напряжения третьего рода, уравновешенные в микрообъемах, соизмеримых с размером кристаллической решетки.
По аналогии с сопротивлением материалов собственные напряжения подразделяют в зависимости от направления действия на одноосные или линейные, действующие лишь по одному направлению в теле; двухосные или плоскостные, действующие по всем направлениям в плоскости; трехосные или объемные, действующие по всем направлениям в пространстве.
В элементах сварных конструкций могут возникать одно-, двух - или трехосные напряжения в зависимости от формы и размеров свариваемых элементов. Напряжения, действующие вдоль
сварного шва, называют продольными и обозначают ах. Напряжения, действующие в плоскости соединяемых элементов перпендикулярно оси шва, называют поперечными и обозначают су. Напряжения, действующие в направлении, перпендикулярном плоскости соединяемых элементов, называют напряжениями по толщине сварного соединения и обозначают az. Наряду с нормальными компонентами в сварных соединениях могут действовать соответствующие касательные напряжения ттуг, тг*.
Деформации, возникающие при сварке, обозначаются аналогично напряжениям. Различают нормальные компоненты сварочных деформаций ех, ву, ег и сдвиговые уХу, уyz, Угх■ Сварочные деформации в общем случае определяют изменение линейных и угловых размеров тела и характеризуют состояние отдельных участков тела. Основные причины, вызывающие появление деформации при сварке, заключаются в неравномерном нагреве, структурных превращениях и упругопластическом деформировании. Поэтому необходимо различать следующие составляющие сварочных деформаций:
1. Свободная деформация, вызванная изменением температуры и структурными превращениями
|
(11.1) |
Єсв — а Г,
где а — коэффициент линейного расширения металла, 1 /К; Т — изменение температуры точки тела, К.
2. Собственные или так называемые внутренние деформации (б, y)> состоящие ИЗ упругих И пластических Є„л, 7пл деформаций.
3. Наблюдаемые в процессе сварки деформации вн, у„, характеризующие изменение линейных и угловых размеров тела, которые можно зарегистрировать непосредственно измерительными приборами. Эти деформации определяются суммой свободных температурных и собственных деформаций
|
(11.2) |
В н — Є св ~|~ В упр "4” В пл J
Ун У упр “Ь У пл.
Уравнения (11.2) могут быть записаны применительно ко всем компонентам деформаций для соответствующих координат. Если в рассматриваемый момент времени в теле уже были предварительные (начальные) деформации Єнач, Уна**»
то уравнения
(11.2) преобразуются к следующему виду:
|
|
(11.3)
Напряжения при сварке однозначно определяются значениями упругих деформаций по следующим формулам:
G* ~ 1 „£Є*УПР Н j _ 2v (В*У"Р еУУпр + єгупр) J;
|
(11.4) |
= 1 fl_ 2v^Sjtynp е»УпР “t - ezY"p)J >
— j ^^Єгупр -| 2V (е*упр + е9упр + 6Zynp)J',
|
Gy 2. |
|
угушр, <■ zx • |
Tty — Gyxyyup, Туг — Gy
где E, G, v — соответственно нормальный модуль упругости, модуль сдвига и коэффициент Пуассона.
Изменение положения или формы конструкции, т. е. искажение конструкции в целом, в результате сварки характеризуется перемещениями. Перемещения при сварке связаны с наблюдаемыми деформациями (11.3) следующими формулами:
|
dU |
|
dV |
|
dW |
|
dx’ Єуя~ dy' £zH~ dz ' |
|
(11.5) |
|
dU, dV dy + ~d7’ Уугк |
|
dlT dy |
|
dV dz |
|
dW. dV, dx dz ’ |
|
+ |
|
У хул ■ |
где U, V, W — перемещения соответственно по осям X, у, Z.
Сварочные деформации и перемещения по аналогии с напряжениями могут быть временными и остаточными. В зависимости от вызываемых искажений формы и размеров конструкции различают следующие виды перемещений: укорочение, изгиб, потеря устойчивости, скручивание и др. Эти (как правило, сложные) перемещения конструкции можно представить в виде суммарного проявления отдельных элементарных видов деформаций в зоне сварных соединений. Поэтому основная задача — умение правильно определить элементарные виды деформаций в зависимости от режимов сварки, жесткости свариваемых элементов и других параметров, которые используются для расчета перемещений конструкции [17].