Равновесие в гетерогенных системах. Растворы
ПРАВИЛО ФАЗ ГИББСА —КОНОВАЛОВА
Гетерогенной называется система, состоящая из отдельных частей, ограниченных физическими поверхностями раздела — фаз. Вещества, составляющие ту или иную фазу, должны присутствовать в количестве, достаточном для того, чтобы поверхностные свойства не определяли их состояние. Гетерогенные системы могут быть построены из одного (однокомпонентные) или из нескольких веществ (многокомпонентные). Число компонентов определяется числом различных веществ, составляющих систему, но, так как они могут реагировать между собой, надо учесть число возможных реакций между ними: число компонентов К равно разности чисел различных веществ в системе и независимых реакций между ними.
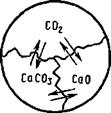
Например, в системе диссоциирующего карбоната кальция (рис. 8.7) есть СаСОз, СаО и С02, между которыми возможна реакция:
СаСОз^СаО + СО2.
Следовательно, для построения данной системы достаточно взять только два вещества, так как третье получится по уравнению реакции:
/(=3-1=2.
Можно взять и одно вещество — СаСОз, но в этом случае система будет эквивалентной, т. е. с наложенным условием для масс СаО и С02.
Числом компонентов называется число различного вида молекул, необходимое и достаточное для построения данной системы.
Параметры состояния гетерогенных систем — температура Т, давление р и концентрации всех компонентов во всех фазах, если они имеют сложный состав.
|
Рис. 8 7. Система диссоциирующего карбоната кальция |
Общее условие равновесия гетерогенных систем — равновесие между всеми их частями — фазами.
|
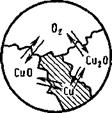
Рис. 8.8. Система оксидов меди, меди и кислорода |
Условия равновесия остаются прежними, т. е. при T=const, р=const
AG—>-0, G—►GmiB.
Однако условие равновесия гетерогенной системы зависит также от ее строения — числа фаз и числа компонентов. Это устанавливает связи между параметрами равновесия, причем некоторые параметры остаются свободными, т. е. могут принимать произвольные значения без изменения строения системы (число фаз). Эта связь между параметрами равновесия и строением системы выражается правилом фаз Дж. В. Гиббса и Д. П. Коновалова, пришедшего к тому же выводу, независимо от работ Гиббса:
С = К + 2 —Ф, (8.54)
где С — число степеней свободы или параметров, которым можно задавать произвольные значения без изменения числа фаз в системе; К — число компонентов; Ф — число фаз в системе.
Примеры применения правила фаз. 1. Рассмотрим систему из меди, оксида меди (I), оксида меди (II) и кислорода (рис. 8.8).
В системе возможны реакции:
1. 2Cu-f025=t2Cu0; 3. CuO-f Си^СигО;
2. 4Си + 02^2Си20; 4. 2Си20+025-4Си0.
Из этих реакций только первые две независимы, а поэтому число компонентов К—4—2=2 (кислород и медь). Число фаз в системе — 4. Число степеней свободы С = 2+2—4 = 0.
Такие системы называются нотариантными и могут существовать только при определенных температуре и давлении. В данном случае при повышении температуры пройдет реакция 3 и СиО как фаза исчезнет, а при понижении температуры исчезнет Си20 по реакции 4.
2. Рассмотрим систему диссоциирующего карбоната кальция:
СаС0з^Са0 + С02 «
Число компонентов К=3—1=2; число фаз Ф=3; число степеней свободы С=2+2 — 3=1.
В этой системе получилась одна степень свободы — система моновариантная. Это означает, что давление рсо, представляет собой функцию температуры:
Р сог= f(T).
Другими словами, р со2— константа равновесия гетерогенной обратимой реакции:
К-рсо-КТ). (8.55)
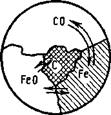
3. Рассмотрим гетерогенную систему восстановления оксида железа оксидом углерода (II) СО (рис. 8.9):
FeOTB-|- CO^FeTB-|- С02.
Рис. 8.9. Система вое - Рис. 8.10. Двух - (б) и трехфазные (а)
становления оксида системы плавления металла
железа оксидом углерода:
FeOTB+ СО, ,,. * Fer, - f
+ со2газ
Число компонентов К=4 —1 = 3; число фаз Ф=3; число степеней свободы С — 3 + 2 — 3—2.
Система получилась бивариантной с двумя степенями свободы. Параметров равновесия 3:Г, р и х, где х — состав газовой фазы
pco=f(T, х). (8.56)
т. е. равновесное давление СО будет зависеть от температуры и количества введенного в газовую смесь СОг. Константа равновесия этой реакции
К,= £&■ = f(T). (8.57)
Правило фаз для тех случаев, когда в системе фиксировано давление, можно записать иначе:
С = К+1 —Ф. (8.58)
Например, если рассмотреть систему плавления чистого металла (рис. 8.10), то можно отбросить газовую фазу, состоящую из насыщенного пара металла, но число степеней свободы не изменится: а — С = К + 2 —Ф = 1+2 —3 = 0; б — С = К+1 — — Ф = 1 + 1 — 2 = 0, т. е. обе системы нонвариантны.
Таким образом, в металловедении все диаграммы плавкости будут представлять собой изобары. По правилу фаз можно определить максимальное число фаз, находящихся в равновесии, положив при этом число степеней свободы С равным нулю.
Нонвариантные системы для данного вещества постоянны (так называемые тройные точки) и по ним судят о чистоте взятого вещества (температуры плавления, температуры фазовых переходов).
КОНСТАНТЫ РАВНОВЕСИЯ В ГЕТЕРОГЕННЫХ
СИСТЕМАХ
Равновесие обратимых химических реакций, протекающих в гетерогенных системах, также рассчитывают, исходя из общих условий равновесия:
при Т = const, р = const AG -* О, G -* Gmin.
Однако в отличие от гомогенных систем для гетерогенных константы равновесия обычно выражаются в парциальных давлениях ftp и не содержат парциальных давлений твердых или жидких (конденсированных) фаз, если эти фазы представляют собой чистые вещества постоянного состава.
Пример 6. Восстановление оксида железа твердым углеродом (прямое восстановление) :
FeOrn -|- Cm ^ FBtb - р СОгаз
В этой системе (рис. 8.И) четыре фазы, состоит она из трех компонентов (4—1) и имеет только одну степень свободы:
'С=/С+2-Ф = 3 + 2-4=1.
Таким образом, в этой системе параметры равновесия рсо и Т связаны между собой соотношением
Рсо = КТ)-
Давления насыщенных паров FeO; С и Fe при данной температуре постоянны и не будут влиять на химическое равновесие и константу равновесия
*р = Рса = КП (8.59)
Вычисление константы равновесия аналогично ранее рассмотренному расчету гомогенных равновесий. Например, для этой реакции:
AG0 = ЛЯ° - TAS0 = - ЯПпК/,;
А Н° = - АН°РМ - А Не + АН°Ре + АН°со = + 263 - 0 + 0 - 110,5 = 152,5 кДж. AS0 = - Spe0 - + S£e + S£0 = - 58,79-5,74 + 27,15 + 197,4 =
- 160,2 Дж/К.
Отсюда AG°= 152 500- 160,02 Г, при Г =1000 К AG0 = - 7520 Дж, AG <0 — реакция возможна.
Находим константу равновесия К
—AG“ 7520
|
Рис. 8.11. Система вое - ста и овлеи ия оксид а железа твердым угле- |
IgA-v - 2>злг - 2,3-8,31 ■ 1000 “°’392;
Кы = 2,465.
Переходим к константе Др(р0= 1,013- 105 Па, a 2 п = 1): К?=КіІр$*=2'465-1,013-105 = 2,497-105 Па.
Пример расчета использует приближенное уравнение, но и при точном расчете порядок счета будет аналогичный.
Пример 7. Восстановление оксида железа FeO оксидом углерода СО (рис. 8.9) происходит по реакции
FeOTB+ COra3^FeTB-f С02газї
В этой системе будет три фазы, число компонентов равно трем (4—1), а число степеней свободы
С=* + 2-Ф = 3 + 2-3 = 2.
Параметры равновесия: Т, рсо, рсо,, а выражение для константы равновесия будет записано так:
К?=р со J Pco=f(T).
|
Kp = (%C02)/(%C0)=/(r). -азовой атмосферы от темпе[ ия энергии Гиббса: Д С0 = ЛЯ° - ГДа° = - ЛГ[(% С02)/(% СО)]; |
Так как реакция идет без изменения числа газовых молей и константа безразмерная, заменим отношение парциальных давлений отношением объемных долей:
Зависимость состава газовой атмосферы от температуры найдем из уравнения стандартного изменения энергии Гиббса:
по аналогичному расчету (см. пример 8.6) уравнение AG0 будет иметь вид AG°=—20 000+15,44 Т;
для температуры 1000 К AG°=— 4560 Дж (AG°<0), определим состав газовой атмосферы:
1;;1%С02) _ —AGf _ 4560 _
s (%СО ) Д-2,37" 8,31-2,3-1000
(%С02) / (%СО) = 1,73 или 36,63% СО и 63,37% С02.
Однако если реагирующие вещества находятся в состоянии раствора в какой - либо конденсированной фазе (жидкий или твердый раствор), то на равновесие обратимых реакций будут очень сильно влиять активные концентрации в растворе.
РАСТВОРЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ
В двух - или многокомпонентных системах могут возникать растворы. Согласно правилу фаз Гиббса — Коновалова, раствором называется гомогенная система (или часть системы — фаза), состоящая из двух или нескольких компонентов.
Обычно растворами называют жидкие или твердые фазы, так как в газообразном состоянии силы взаимодействия между молекулами очень слабы и называем их газовыми смесями. При состоянии газа, близком к критическому, возможно образование растворов (Гкрит; р Крит) • ,
Взаимодействие частиц растворенного вещества и растворителя приводит к изменению их свойств и создается новая система — раствор. Процесс образования растворов энергетически обусловлен. Во-первых, при образовании раствора резко увеличивается энтропия: As—энтропия смешения (см. п. 8.2) больше нуля. Во-вторых, при взаимодействии частиц между собой и при образовании комплексов между ними изменяется энтальпия системы ДЯ<0.
Изменение энергии Гиббса при растворении
AG =АН — TAs.
Если при образовании раствора поглощается энергия и АН > 0, то энтропия растворения всегда больше нуля и процесс самопроизвольного растворения возможен (криогидрат - ные растворы).
|
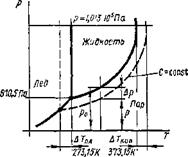
Рис. 8.12. Фазовая диаграмма воды (сплошная) и водного раствора (штриховая линии) для постоянной концентрации (С = const) |
Физические свойства новой системы — раствора отличаются от свойств растворителя, так как растворенное вещество, образуя с ним комплексы, понижает его активность и, в частности, всегда понижает упругость его пара (Рауль), а это приводит к изменению температуры кристаллизации и температуры кипения.
На рис. 8.12 приведена фазовая диаграмма воды, в которой тройная точка (нонвариантная система) обладает координатами: Г=273,15 К, р=610,5Па. Температура кипения при давлении 1,013-105Па соответствует 373,15 К. Введение растворенного вещества (второй компонент) увеличивает число степеней свободы и константные точки растворителя начинают смещаться в зависимости от концентрации растворенного вещества. На этой же диаграмме штриховой линией нанесена кривая давления насыщенного пара над водным раствором некоторой постоянной концентрации С = const. Пересечение штриховой кривой с изобарой р= 1,013-105 Па произойдет при температуре выше 373 К, а с кривой давления пара надо льдом — ниже 273,15 К. Все изменения константных точек могут быть вычислены или определены экспериментально. Для разбавленных растворов они прямо пропорциональны числу молей растворенного вещества. Расчетные уравнения, известные из курса химии [29], приведены ниже.
Понижение давления насыщенного пара
Ро—р Ар п. Ар п
~~ р А/’
|
n+N’ |
(8.60)
|
Ра |
Р о
где ро — давление пара над чистым растворителем; р — давление пара над раствором; п — число молей растворенного вещества; N — число молей растворителя.
Понижение температуры кристаллизации
|
т-1000 Mg ' |
|
(8.61) |
|
кр |
|
АТю=То—Т=К |
где То — температура кристаллизации растворителя; Т — температура кристаллизации раствора; Ккр—константа кристаллизации (криоскопическая); m — масса растворенного вещества; М — его молекулярная масса; g — масса растворителя.
Повышение температуры кипения
АТт-Т-То=К^^^-, (8.62)
где /(кип—константа кипения (эбуллиоскопическая), а остальные обозначения те же.
Значения констант для некоторых веществ приведены в табл. 8.5.
Растворы относятся к конденсированным системам (жидкие, твердые) и поэтому силы взаимодействия между частицами растворенного вещества и растворителя, а также силы взаимодействия между частицами самого растворенного вещества достаточно большие. Это приводит к тому, что как бы уменьшается число частиц в растворе, способных самостоятельно перемещаться и участвовать в процессе, т. е. уменьшается активность растворенного вещества. Это можно учесть, введя понятие коэффициента активности у. Тогда активная концентрация, или просто активность, будет равна
а=ус, (8.63)
где а — активность; у — коэффициент активности; с — концентрация в растворе, выраженная в соответствующих единицах.
Коэффициент активности чаще всего определяется экспериментально, путем сравнения полученного эффекта с теоретически ожидаемым, например:
У=А7’ЭКСП/АГ
теор*
(8.64)
Значение коэффициента активности зависит от температуры, природы раствора и его концентрации. В водных растворах малой концентрации у—>-1.
Для металлических растворов у<1 и изменяется в зависимости от концентрации, а поэтому пользуемся диаграммами плавкости, построенными на основании экспериментальных данных. Как известно по диаграммам плавкости, между растворенным металлом и металлом-растворителем (матрицей) могут возникать не только комплексы переменного состава, но и химические соединения — интерметаллиды.
Упругость насыщенного пара над растворами. При испарении растворов в целом ряде случаев необходимо учитывать не только
|
Таблица 8.5. Значения констант закона Рауля дли некоторых веществ
|
|
Рис. 8.13. Схема испарения двухкомпонентного раствора |
|
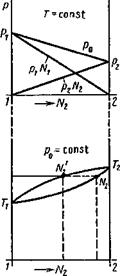
Рис. 8.14. Зависимость давления насыщенного пара (Т = const) и температуры кипения (Ро = = const) от концентрации (N,) идеального раствора |
упругость пара растворителя, но и общую упругость пара, включая и упругость пара растворенного вещества, которая зависит, естественно, от коэффициента активности его в данном растворе.
Рассмотрим так называемый идеальный раствор, в котором можно пренебречь силами межмо - лекулярного взаимодействия. В этом случае общая упругость пара над раствором будет равна сумме парциальных упругостей пара всех отдельных компонентов раствора:
|
(8.65) |
к
ра= ірі,
где р0 — общая упругость пара над раствором; р, — упругость пара данного компонента раствора в его свободном состоянии; Ni — молярная доля компонента в растворе.
Для бинарного раствора можно написать:
ро=Лґі/7і+ЛҐ2р2, (8.66)
где Ni я N2 — молярные доли компонентов в жидком растворе. Найдем молярные доли компонентов в газовой фазе N[, N'2:
|
NjPi |
|
N{ = |
|
(8.67) |
|
m-- |
|
Po |
|
Nipi + N2P2 po ' N 2p2 N2P2 |
|
Nlpl + N2p2 |
|
Nipi. |
Из системы уравнений (8.67) видно, что молярные доли в жидкости и в парах совпадут только при условии, если упругости пара над чистыми компонентами будут равны и будут равны их молярные доли, Т. е. N1—N2; pl=p2. Во всяком другом случае
доля компонента в парах не будет совпадать с его молярной долей в жидкости.
Рассматриваемая система (рис. 8.13) обладает двумя степенями свободы С=2+2—2—2, а условия равновесия будут определяться уравнениями:
|
(8.68) |
ро=КТ, С);
T^=f{p0, С),
где С — концентрация раствора.
Графически эти зависимости можно представить двумя диаграммами, приведенными на рис. 8.14.
Этими свойствами систем обусловлена разгонка жидкостей, а также потеря легколетучих компонентов сплавов, содержащих Mg, Zn, Мп, при сварке плавлением.
Если учесть силы межмолекулярного взаимодействия между испаряющимися молекулами компонентов, то может быть два случая:
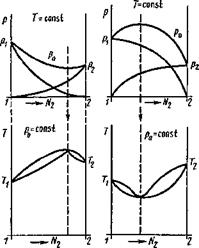
1. Молекулы компонентов образуют между собой связи, мешающие им переходить в парообразное состояние. В этом случае (рис. 8.15,7) кривая упругости пара р0 имеет минимум, а кривая температур кипения при заданном ри имеет максимум. Петля гистерезиса разделяется на две части, а для состава, отвечающего максимуму температуры кипения, будет наблюдаться постоянство Nt=N! и раствор будет переходить в пар без изменения состава. Такие растворы
носят название азеотропних. j ж
|
|
2. Молекулы компонентов способствуют друг другу переходить в парообразное состояние. В этом случае на кривой ро наблюдаем максимум, а на кривой Ткш — минимум, как это показано на рис. 8.15, II для определенного состава раствора. Этот раствор также будет азеотропним, т. е. кипящим без изменения состава.
В сварочной технологии применяются некоторые азе - отропные растворы. НИИав - тоген предложил азеотропний раствор ортометилбора - та В (ОСНз)з и метилового спирта. Этот раствор используют как газообразный флюс Рис - 8.15. Зависимость давления насы-
при сварке сплавов цветных "!,епннога0 f„pa и тем,,ературы
^ ^ ч кипения (ро sss const) для азеотропных
металлов (латуни, бронзы). растворов, имеющих максимум (/) или При введении ЭТОГО раствора минимум температуры кипения (II)
в пламя кислородно-ацетиленовой горелки B2U3, полученный при сгорании раствора, тонким слоем закрывает сварочную ванну и повышает качество сварных соединений.
Распределение компонента между жидкими фазами. Концентрации одного и того же компонента в двух сосуществующих фазах различны, но функционально связаны между собой. Соотношение концентраций компонента в двух сосуществующих равновесных фазах определяется законом распределения, который для самого простого случая может быть записан так:
L=ci/C2—const при 7’=const. (8.69)
Более сложные случаи возникают тогда, когда компонент при переходе из одной фазы в другую меняет свое молекулярное строение. В этом случае закон распределения имеет вид
пАт 5===±. тАп фаза 1 фаза 2
L=(ci)л/(с2)т=const при 7’=const. (8.70)
В металлургических процессах при сварке нежелательные примеси (оксиды, сульфиды и фосфиды) извлекаются с помощью шлаковых фаз, растворимость в которых для этих соединений гораздо выше, чем в жидких металлах. Полнота извлечения зависит от свойств шлака, его относительного объема и коэффициента распределения (см. гл. 9).
Зависимость коэффициента распределения от температуры обычно выражается экспонентой: LT—Loe~AmTl
Растворимость газов в жидкостях. В системе раствор газа — газ (рис. 8.16) имеются две фазы и два компонента (газ и растворитель): С=2+2—2=2, т. е. система имеет две степени свободы и концентрация растворенного газа будет функцией температуры и давления газа над жидкостью. Положим 7=const, тогда
І=(Л2) г/ (А2) ж= const.
|
Рис. 8.16. Схема растворимости газа в жидкости |
Концентрация газа в газовой фазе может быть вычислена по уравнению состояния газа:
(Л2) f=nAJv=pA Л#т)-
Подставляем это выражение в уравнение константы распределения, получим
Т _ РАг
или
(A2)m=PaALRT) или (A2)*f=KtPa» (8-71)
где Кт—константа растворимости, зависящая от температуры:
KT=Koe-^/(Rn
|
(8.72) |
Здесь АН — разность энтальпий при растворении.
Если с растворителем контактирует смесь газов, то каждый газ будет растворяться пропорционально своему парциальному давлению (закон Генри—Дальтона).
Растворимость газов зависит от строения и характера связей в их молекулах. Так, в воде, молекулы которой обладают высокой полярностью, неполярные молекулы (Нг; N2; Ог) растворяются ограниченно, но газы, обладающие высокой полярностью (NH3, НС1), растворяются весьма сильно и не подчиняются закону Генри—Дальтона, так как они химически взаимодействуют с водой (НС1 диссоциирует на ионы Н+ и С1 , а аммиак образует комплексное соединение NH4OH).
Растворимость газов в металлах. Жидкие и твердые металлы, а также системы, образованные в результате металлической связи, могут растворять в себе газы только в атомарном состоянии, причем те, которые имеют в атомах непарные электроны (Н; N), но не образующие ионных связей с металлами, как это характерно для активных- окислителей (F, С1). В малоактивных металлах кислород может растворяться без образования оксидов (Au; Ag). Инертные газы, атомы которых не имеют неспаренных электронов, в металлах растворяться не могут. Кислород растворяется в металлах в виде своих соединений, обладающих металлообразным характером (субоксиды d-металлов, низшие оксиды d-металлов, обладающие металлической проводимостью).
Растворение водорода и азота в металлах сопровождается диссоциацией молекул этих газов на атомы:
Н2^2Н, KP=&=f(T),
Р н,
отсюда парциальное давление атомарного водорода
р Н= т/КррНг
Подставляем значение парциального давления атомарного водорода в уравнение (8.71) и получаем
[Н] = К' ІЩр^= КтРК (8.73)
Это уравнение впервые было получено Сивертсом. Зависимость растворимости водорода от температуры определяется знаком АН растворения:
KT=Koe-^/(RT). (8.74)
Процесс диссоциации молекул газа идет всегда с затратой энергии Д#диС>-0, и растворимость водорода и азота с повыше-
|
(8.75) |
|
ниєм температуры увеличивается: |
ЛЯ _ d(uK7)^ n JtT1 dT >
Если водород и азот образуют с металлом устойчивые соединения (гидриды или нитриды), то в этом случае общая энтальпия растворения может быть меньше нуля и с повышением температуры растворимость будет уменьшаться (см. гл. 9).