Приложение первого начала термодинамики к химическим процессам
ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ
Термодинамика — наука об энергии и ее изменениях; область ее применения необычайно широка.
Химическая термодинамика — самостоятельная часть общей науки об изменениях и переходах энергии; в ее основе лежат
главным образом два закона, известные из курса физики: первый закон термодинамики, представляющий собой закон сохранения материи и энергии, сформулированный в 1756 г. М. В. Ломоносовым, и второй закон термодинамики, позволяющий судить о возможности самопроизвольного развития процессов в данных физических условиях. Не довольствуясь общими феноменологическими уравнениями термодинамики, химическая термодинамика дополняет их квантово-механическим учением о строении вещества, привлекает статистический метод и этим значительно расширяет возможности исследования сложных материальных систем.
Под термодинамической системой понимают комплекс физических тел, находящихся во взаимодействии между собой, мысленно обособленный от окружающей среды.
Таким образом, термодинамическая система может взаимодействовать с окружающей средой.
Изолированной системой называется система, у которой запрещен энергообмен и массообмен с окружающей средой: 2М = = const; 2 Е = const.
Замкнутая система может иметь энергообмен с окружающей средой, но массообмен запрещен: 2Af = const; 2£^=const.
Незамкнутые системы рассматриваются в особом разделе термодинамики — термодинамика неравновесных систем: 2Af=^= =5^const; 2const.
По своему строению термодинамические системы могут быть гомогенными, т. е. однородными, если нет границ раздела между отдельными их частями (газовые смеси, растворы), или гетерогенными, в которых существуют границы раздела между отдельными частями системы — фазами, отличающимися друг от друга или химическим составом, или физическими свойствами, обусловленными строением (твердое тело — жидкость — пар и т. д.).
Таким образом, фазой называется часть гетерогенной системы, отделенная физической границей раздела, т. е. границей резкого изменения свойств. Так как всякая граница раздела обладает запасом свободной энергии, то в системах высокой дисперсности свойства поверхностей раздела будут влиять на состояние системы и даже доминировать над объемными свойствами. Так, при высоком дроблении твердых или жидких фаз изменяются их температуры плавления, температуры кипения. Высокодисперсные системы могут создавать метастабильные системы — коллоидные растворы и аэрозоли. К таким системам общие термодинамические закономерности уже не приложимы.
Совокупность всех свойств термодинамической системы определяет ее состояние.
Любая физическая величина, влияющая на состояние системы — объем, давление, температура, внутренняя энергия, энтальпия или энтропия, — носит название термодинамического параметра или просто параметра. Для наиболее простой системы — идеального газа — можно ограничиться двумя параметрами Т
и р, так как молярный объем v определяется из уравнения состояния газа.
Изменение хотя бы одного параметра состояния приводит к изменению всей системы, называемой термодинамическим процессом.
Последовательное изменение состояния системы, в конечном итоге приводящее ее вновь в исходное состояние, называется круговым процессом или циклом.
Термодинамические процессы следует разделять на обратимые и необратимые. Обратимым процессом называется такой процесс, который, будучи проведенным в прямом и обратном направлениях, не оставляет никаких изменений в окружающей среде. Обратимый процесс можно рассматривать как сумму бесконечно близких равновесий, когда бесконечно малое изменение параметров (внешних условий) может изменить направление процесса. Поэтому истинно обратимый процесс может совершаться только с бесконечно малой скоростью, с тем чтобы соблюдалось условие равновесия или обратимости.
Обратимый процесс можно отождествить с термодинамическим равновесием, т. е. с таким состоянием системы, при котором взаимно компенсированные процессы не приводят к изменению состава и параметров системы.
Работа, совершаемая обратимыми процессами, — максимально достижимая, так как при изменении направления процесса энергия не расходуется на изменения, остающиеся в окружающей среде.
В термодинамике различают также однородные и неоднородные системы, подразумевая под этим равномерное или неравномерное распределение свойств (концентрации, плотности, температуры, давления) по объему фазы.
Неоднородные системы — неравновесные и в них всегда возможно возникновение необратимых процессов, таких, как теплопередача, диффузия и т. д. Такие системы рассматривает термодинамика необратимых систем, используя уравнения математической физики (Фурье, Фика и др.). Эта область термодинамики в настоящее время получила большое развитие благодаря широкому применению ЭВМ.
ФОРМУЛИРОВКА ПЕРВОГО НАЧАЛА
ТЕРМОДИНАМИКИ
Первое начало термодинамики, окончательно сформулированное Джоулем в середине XIX в., представляет собой закон сохранения энергии. Для замкнутых систем, способных обмениваться энергией с окружающей средой, уравнение первого закона термодинамики имеет вид
Q = MJ+A, (8.1)
где Q — энергия, полученная системой из окружающей среды;
ДU — увеличение внутренней энергии системы; А — совершенная системой работа.
Уравнение (8.1) исключает возможность получения какой - либо дополнительной работы или построения вечного двигателя — perpetuum mobile 1-го рода невозможен.
Внутренняя энергия системы U, приращение которой Д V считается положительным при Q>/4, представляет собой весьма сложную термодинамическую функцию.
Внутренняя энергия U включает в себя все виды энергии в веществах, составляющих систему, кроме энергии, созданной гравитационными, электрическими или магнитными полями, а также кроме кинематической энергии системы в целом (для движущейся системы).
Внутренняя энергия представляет собой термодинамическую функцию, полностью определяемую состоянием системы или определенным сочетанием параметров р, v, Т.
Поглощенная энергия Q, так же как и работа А, совершаемая системой, характеризуют процесс изменения системы, и от начального и конечного состояния системы они зависят неоднозначно, так как из начального состояния системы можно перейти в конечное различными путями с различным изменением энергии или работы.
Поэтому уравнение (8.1) записано в конечных разностях, а не в дифференциальной форме. В дифференциальной форме его можно записать только в том случае, когда известен закон изменения параметров состояния и их соотношения.
В общем виде для бесконечно малых изменений состояния системы уравнение первого закона термодинамики можно представить в следующей форме:
|
(8.2) |
bQ = dU + bA,
где 6Q—бесконечно малое изменение энергии системы, положительное при поглощении энергии системой; dU — полный дифференциал внутренней энергии системы; 6/4 — бесконечно малая работа, положительная, если она совершается системой.
Иэохорический процесс (v=const) изменения давления и температуры определяется законом Гей-Люссака (р/Т = const; V — const). При изохорическом процессе работа системы будет равна нулю:
6/4 = pdv = 0. Следовательно, уравнение (8.2) принимает вид
|
(8.3) |
dQ = dU.
Вся поглощенная системой энергия идет на увеличение запаса внутренней энергии. Для идеального газа можно написать, что
|
|
(8.4)
где cv — молекулярная теплоемкость при постоянном объеме. Расчетным уравнением для вычисления изменения внутренней энергии при изменении от состояния 1 до состояния 2 будет:
2 2 2
^dQ— ^dU = J cvdT (для идеального іаза), или
і і і
Ql,2=U2-Ui = cv(T2-Tl). (8.5)
ЭНТАЛЬПИЯ КАК ТЕПЛОВАЯ ФУНКЦИЯ
Изобарический процесс (p = const). Изменения объема газа и температуры происходят по закону Гей-Люссака (v/T= const при р = const). Первый закон термодинамики в этом случае будет иметь следующий вид:
dQ = dU + dA = dU + pdv. (8.6)
Энергия изобарического процесса для изменения состояния 1—2:
Qi.2 = (U2 + pv2) — {Ui + pv). (8.7)
Выражение в скобках принимаем за новую термодинамическую функцию — энтальпию Н, которая равна энергии, необходимой для приведения системы в данное состояние, в том числе изменению внутренней энергии и внешней работе. Таким образом, изменение энергии можно представить так:
Qi,2 = //2 —Я, = ДЯ, (8.8)
где Я2 — энтальпия конечного состояния системы; Я і — энтальпия начального состояния системы.
Изобарические процессы наиболее часто встречаются в области высоких температур, в частности в металлургии сварки.
Рассмотрим изменение энтальпии реальных веществ, которые могут менять свои фазовые состояния и теплоемкость которых зависит от температуры и скачкообразно изменяется в момент фазовых переходов. В общем виде уравнение для расчета энтальпии реального вещества, имеющего одно фазовое превращение в твердом состоянии, будет следующим:
Гпр гпл
ДЯТ=ДЯ0+ $ c{fl)dT + ДЯа„р„р+ $с(рР)<*Г +
|
+ ДЯПЛ+ $ с<ж)гіГ + ДЯЙСП+ $c<r)d7 (8.9) Тпл 7"кнп |
где ДЯо — энтальпия моля вещества при Г=0К; ДЯаврпр, ДЯПЛ, ДЯисп — энтальпия перехода моля вещества из одного фазового состояния в другое (скрытые теплоты перехода) при температуре данного фазового превращения; с(ра), с(,Ч с£ж), с£г) — молярные теплоемкости вещества в зависимости от его фазового состояния.
Теплоемкость — основное энергетическое свойство вещества, зависящее от его строения и температуры.
Теплоемкости определяются экспериментально (калориметрически), но они могут быть и вычислены теоретически, исходя из строения элементарных частиц и всего вещества в целом с достаточной степенью точности. При расчете теплоемкостей и энтальпий газов при высоких температурах, когда поглощение энергии газообразным веществом происходит вследствие возрастания •энергии поступательного движения молекул, вращательного движения сложных молекул, колебательного движения атомов внутри молекул и расхода энергии на возбуждение электронных оболочек атомов, а в случае высокотемпературной плазмы (-—-106 К) и на возбуждение ядерных структур (термоядерные реакции). Суммируя все расходы энергии, можно в общем виде представить уравнение теплоемкости газа следующим уравнением:
Ср— R "I - Сп-|- С вр—[- С кол-!- £ эл-!- С я, (8.10)
где R — газовая постоянная; с„—теплоемкость поступательного движения; свр—теплоемкость вращательного движения, по Максвеллу; скол— теплоемкость колебательного движения внутри молекулы, по Планку — Эйнштейну; сэл—часть теплоемкости, идущая на возбуждение электронов; ся—часть теплоемкости, идущая на возбуждение ядра.
Для удобства пользования при расчетах температурные функ-
|
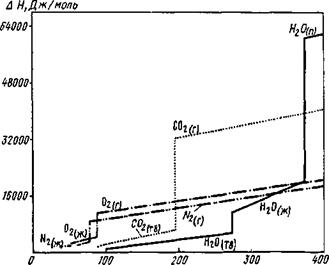
Т, К Рис. 8.1. Изменение энтальпий газов в зависимости от температуры |
ции теплоемкостей выражают уравнениями: ср=а + ЬТ + cT2 + dT3 или (8.11)
ср=а + ЬТ + с'Т~2.
Коэффициенты этих уравнений, необходимые для расчета энтальпий, приводятся в справочниках. Изменение энтальпий некоторых газов в зависимости от температуры приведено на рис. 8.1.
СТАНДАРТНЫЕ УСЛОВИЯ И ТЕРМОХИМИЧЕСКИЕ
РАСЧЕТЫ
При металлургических и термодинамических расчетах пользоваться абсолютными значениями энтальпий (8.9), отсчитываемых от О К, нет особой необходимости. Можно установить другой уровень отсчета, более удобный и более определенный, так как в реальных расчетах нас интересуют лишь разности энтальпий перехода системы из одного состояния в другое.
За такой условный уровень отсчета приняты стандартные
условия: Т = 298,15 Я = 25°С; р—1,013-105 Па (нормальное атмосферное давление, равное 760 мм рт. ст.).
Стандартная разность энтальпий будет
k 298,15 k
ДЯ°=Я°-Яо=2 S cfdT+ 2АЯіпр, (8.12)
і— 1 0 i^l
где Я0 — энтальпия при стандартных условиях, вычисленная по уравнению (8.9); Яо — энтальпия при абсолютном нуле.
Стандартные разности энтальпий, или, как их часто не совсем правильно называют, стандартные энтальпии, рассчитывают на 1 моль вещества и выражаются в кДж/моль. Для упрощения расчетов сделаны следующие допущения:
1. Стандартные разности энтальпий простых веществ в состоянии, устойчивом при стандартных условиях, принимают равными нулю.
Например: ДЯн2=0, а ДЯн=217,9 кДж/моль, так как при стандартных условиях водород устойчив в виде молекул Нг, а для получения атомарного водорода надо затратить энергию, т. е. увеличить энтальпию на 217,9 кДж на 1 моль атомарного водорода.
2. Стандартные разности энтальпий сложных веществ равны обратному по знаку тепловому эффекту реакции (—Q,) образования их из простых в состояниях, устойчивых при стандартных условиях. _
Для экзотермической реакции тепловой эффект реакции Qp больше нуля, но так как энергия выделяется в результате уменьшения энтальпии, то ДЯ<0. Для реакций эндотермических Qp меньше нуля, но разность энтальпий ДЯ>0, так как поглощенная энергия увеличивает энтальпию системы Например, ДЯн, о= = —285,83 кДж/моль; ДЯ°мо= +91,26 кДж/моль.
В настоящее время в расчетах тепловые эффекты не используются и в справочной литературе приводятся данные только по разностям энтальпий. Изменения энтальпий системы при совершении химической реакции в ней рассчитывают следующим образом: стандартные разности энтальпий начальных продуктов учитывают со знаками минус, а конечных продуктов реакции — со знаком плюс. Например, чтобы определить разность энтальпий реакции сгорания ацетилена, по справочным данным находим:
ДЯ£2н2== +226,75; ДЯ^г0г1 =—241,82; ДЯ£0г = —393,51 кДж/моль. Запишем уравнение реакции горения ацетилена:
С2Н2 + 5/202=2С02 + Н20 ДЯ°Реакц= -226,75—0 -2X393,5-241,82 =
= — 1255,57 кДж на 1 моль С2Н2.
Если необходимо вычислить разность энтальпий какой-нибудь химической реакции при условиях, отличающихся от стандартных, то тогда надо учесть зависимость разности энтальпий от температуры. Это можно сделать по следующим уравнениям: для газообразных веществ
т
ДЯт=ДЯ0 + 2гс $ cf'dT, (8 13)
298,15
где Z/г — сумма коэффициентов реагирующих веществ, причем начальные продукты берутся со знаком минус; с^г) — теплоемкость данного вещества в зависимости от температуры (из справочных данных).
Например, для реакции горения водорода можно записать:
2Н2 + 02=2Н20г
т т т
ДЯт=ДЯ°- 2 $ Cf7dT — $ cp°tfr+ 2 $ c*7°dT
298,15 298,15 298,15
для веществ, находящихся при стандартных условиях в жидком или в твердом состоянии, кроме учета нагревания системы г
( 5 cvdTj, необходимо ввести поглощение энергии на измене-
' 298,15 '
ние агрегатных и фазовых состояний (АЯпр). В этом случае уравнение будет более сложным:
г
ДЯг=АЯ° + 2/г $ CpdT + ZnAH^ (8.14)
298,15
где АЯ„Р—для начальных продуктов учитывают со знаком минус, а для конечных продуктов — со знаком плюс.
|
Таблица 8.1. Значение разностей энтальпий некоторыхвеществ при стандартных условиях
|
Для многих веществ интегралы с теплоемкостями просчитаны и приведены в справочной литературе в виде таблиц с графой (Яг—//298,15) для различных температур. Пользование такими таблицами существенно облегчает расчет.
Пример 1. По данным, приведенным в табл. 8.1, определить разность энтальпий приведенных ниже реакций и их эндо - или экзотермичность.
1) СО + Н20Пар= СОг + Н2; 2) Fe0 + C0=Fe + C02; 3) Fe30, + 4C0 =
= 3Fe + 4C02;
4) 2Fe0+Si = 2Fe + Si02; 5) ТіСЦ + 2Mg = 2MgCl2 + Ti;
6) 2Fe0 + Ti = 2Fe + Ti02.
Пример 2. Определить ДЯ° реакции образования водяного пара при температурах 1000 и 2000 К, зная уравнения температурной зависимости теплоемкостей газов, участвующих в реакции, пользуясь табл. 8.1. Значения коэффициентов уравнения теплоемкостей приведены ниже:
|
Газ............ |
. . . . Н2 |
о2 |
н2о |
|
а........................................ |
.... 27,28 |
31,46 |
30,0 |
|
Ь-103 . . . . |
. . . . 3,26 |
3,39 |
10,71 |
|
с'-Ю-5 . . . |
. . . . 0,502 |
—3,77 |
0,33 |
Для уравнения реакции 2Н2 + 02= 2Н20„ напишем формулу (8.13) полностью: т т
ДЯг=ДЯ°+2п $ срЯ7 = ДЯ° + $ (—2с?‘-c°’+2c">°)dT.
298,15 298,15
Определяем ДЯ°= — 0—0—2Х 241,84= —483,68 кДж= — 483 680 Дж.
Загіишем уравнения теплоемкостей с учетом числа молей:
- 2срн’ = - 27,28 • 2 -3,26 • 2 • 10~3 • 7 - 0,502 • 2 • 105 • Г~[4];
-с°'=-31,46-3,39-10_3-7 + 3,77-105-7-2;
+2 = + 30,0 ■ 2+10,71 • 2 • 10-3 • 7+0,33- 2-Ю5 • Г~2;
Подставляя указанные в условии температуры, получим ответы: Д#юоо =
— —495 933 Дж; Д//2ооо = —505 664 Дж.
Следует обратить внимание на весьма небольшое изменение разности энтальпий реакции в зависимости от температуры:
ДЯго^Д— 100% =4,64%.
Таким образом, для ориентировочных расчетов можно пользоваться стандартными значениями разности энтальпий, если абсолютная величина их ~400 кДж. Если абсолютная величина разности энтальпий будет меньше, то относительная ошибка будет больше.