Механика трубопроводов и шлангов

Уравнения малых колебаний абсолютно гибких стержней (нитей) с потоке воздуха или жидкости

Вывод уравнений. Уравнения малых колебаний абсолютно гибких стержней, находящихся в потоке воздуха или жидкости, могут быть получены как частный случай из уравнений системы

(24.30) — (24.36) или (24.49) — (24.54). Выведем их из общих векторных нелинейных уравнений движения абсолютно гибких стержней (23.3) — (23.5), что более наглядно. В безразмерной форме записи было получено следующее уравнение движения нити [см. выражение (23.3)]:

'г“7^1Г+"(*>•» где <2= V (±^1 ^ = 2 ($л 1 ; й-^Я, в, = 2 '

В проекциях на неподвижные оси из (25.1) получаем систе­му уравнений

Х колебаниях

(Зі=(?10-}-Д^: х,—хл--ил/ т

Поэтому после подстановки (25.3) в систему (25.2) и сокращения слагаемых, характеризующих статику, получаем

Где

От — осевое усилие в нити в статике с учетом действия потока, полученное при решении нелинейных уравнений равновесия стсржня (§ 14).

Выражения для слагаемых полных компонент Ас]аХ[ аэроди­намической силы Лб/р получены в § 20 В приложениях №№ 1—5 даны элементы матриц А'3 которые входят в векторные записи аэродинамических сил Ад^ Аць и дк.

Система из трех уравнений аэроупругих колебаний гибкой ннтн (25.4) содержит четыре неизвестные функции: Л0((е, т), *4,(6, т) при 1=1, 2, 3 Поскольку нить считается нерастяжимой, то имеем следующие соотношения, соответственно в статике и в динамике’

(25.5)

Учитывая малость величин их (є, т), из (26.5) и (25.6) мож­но получить следующее соотношение:

(25.7)

В результате полная система уравнений пространственных колебаний нерастяжимой инти в потоке примет вид

+й%+ ^ ^

О (к = 1, 2, 3). (25.9)

Система (25.8) — (25.9) для случая, когда концы шгги непо­движны, решается при краевых условиях

«хк(0, т)=к^к(1, £)=0. (25.10)

Возможна еще идна форма записи уравнений малых колеба­ний абсолютно гибких стержней. Рассмотрим выражение для ди*

Д£.г,=Ою +Щг(/=1, 2, 3). (25.11)

Эти соотношения с учетом уравнения (25.9) позволяют опре­

Делить Д<21:

(25.12)

Исключив Д(2[ из соотношений (25.11), получаем систему трех дифференциальных уравнений вида

О^о) Д(3 +/,о*П. йд + ^№0. дд о - Л <3ш ‘т Сю О. о

^ + -| (25.13)

TOC o "1-5" h z де Ою От |<?ю

^''^+-10^3°-АС1,+-2г^-лд,,--д<з*,=о.

* Т 0,о От <?1г-

В результате, переходя к векторной форме записи, получаем

Систему двух дифференциальных уравнений:

_^ + С0Д<7, = 0; (25.14)

= А^,

Определив из системы (25.14) — (25.15) и и Дфс, находим динамическое осевое усилие нити из соотношения (25.12) Определение частот и форм колебаний для частного случая; когда скорость потока равна нулю (Д<7„ = 0). В этом частном случае свободных малых колебаний инти, нагруженной только силами тяжести, система уравнений (25.14) распадается на си­стему четырех уравнений колебаний нити в вертикальной пло­скости и двух уравнений колебаний нити относительно верти­кальной плоскости. Уравнения колебаний нити в вертикальной плоскости имеют внд

(25.16)

Уравнения колебании нити относительно вертикальной иле СКОСТИ (х_о' = 0) следующие:

ЛОг.=0;

(25.17)

Входящие в уравнения (25 16), (25.17) функция, характери­зующие статику стержня х'0 и фю для случая, когда стержень нагружен только силами веса, определяются из соотношений

Где Сз=С, БІ] С2. Произвольные постоянные С н С,2 находятся из уравнений

1 —хїк — 2с ^сіі 1 ^ ;

1 = сг |^ьИ А--- -|- с^1 — яЬ г2|

В зависимости от координат Хщ точки закрепления правого кон­ца нити.

В качестве примера численного определения частот и форм колебаний рас­смотрим систему уравнений (25 16) при безразмерных координатах точки зак­репления правого конца нити, равных

Лік = 0,6; хчк 0,4.

Воспользовавшись методом начальных параметров, из системы (25.19) определяем частоты и соответствующие им собственные функции (формы) У2*К ?з и ¥4^ (принято ~ «]^; — 44^) соответственно для

Их, » иХі » ЛС».-,с> В результате численного решении уравнений

(25.19) находим частоты

),! Х2 Х. Ч >-4 X - /«

2,643 4,572 6,510 8,492 10,300 12,078

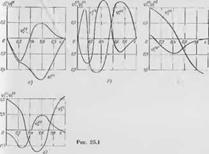
Графики собственных функции соответствующие первым двум час­

Тотам, приведены на рис. 25.1.

Определение частот и форм пространственных колебаний аб­солютно гибкого сгержнм, находящеюся в потоке. Как показано в гл. III, поток воздуха или жидкости может сильно изменить равновесную форму нити и оссвое усилие, что должно привести и к изменению частотного спектра нити.

При проектировании многих реальных конструкций необхо­димо знать области возможных значений частот в зависимости

От направления воздушного потока а (который может быть про­извольным) н его скорости ёо-

Необходимость возможно более полного и точного определе­ния динамических характеристиь (в частности, определения частотного спектра) вызвана многочисленными случаями опас­ных вынужденных колебаний кабелей, тросов, проводов линий электропередач и других гибких элементов конструкций, взаи­модействующих с потоком жидкости или газа. Знание частотно­го спектра в зависимости от параметров потока позволяет про­гнозировать возможные резонансные колебания как при сило­вом, так и при кинематическом (в зависимости от реальных ус­ловий эксплуатации) возбуждении. Кроме того, знание собствен­ных частот н соответствующих нм собственных форм колебаний необходимо для прпближеппых методов исследования автоко­лебаний гибких элементов конструкций, находящихся в потоке жидкости или 1аза. Интерес к задачам о взаимодействии упругих элементов конструкций с потоком жидкости или газа в последние годы резко повысился в связи с возможностью их ре­шения с применением новейшей вычислительной техники. Как правило, эти задачи далее в линейной постановке требуют боль­шого объема вычислительных работ и без применения ЭВМ не могут быть доведены до конца. Этим объясняется тот факт, что ранее опубликованные работы, относящиеся к колебаниям тро­сов и проводов, посвящены частным случаяVI [4; 3; 13], имею - т 1М ограниченное практическое применение. Например, задачи

О колебаниях ниш (провода) в потоке ограничивались рассмот­рением частного случая, когда скорость потока параллельна плоскости, в которой находится провод, в то время как в реаль­ных условиях направление потока произвольно.

Полагая

И=11ф1^ дул - =ДС? до£,/рт, (25.20)

Из системы уравнений (25.14) получим (при Д</=Д#а=0) где 1Й+С^- =0, (25.21)

№—Х'{иХ1 о, Их, о, иХас, ДРх. о, ДРЛао);

Решая уравнение (25.21) методом начальных параметров, определяем частоты колебаний (5, (из условия их/ (1)=0 при /=1, 2, 3) в зависимости от направления потока и его скорости и получаем собственные функции

<р„' (е)=£,.4(е, 4- ууу-т *Л(е, {у (*=1, 2,...,6),

*15(1. Р,)*м(1. Р7)-*|Ь(1. *->5(1. ?,)

~*ы(1. рр*25(1. РУ>— *!£.(!. ?,)

__ ^1(/г-’4— ^14^26 .

^14^25 —

У]—~

— элементы фундаментальной матрицы решений К системы уравнений (25.21), удовлетворяющей условию Л'(0)=£. Произ­водные собственных функций <?(/) можно получить из системы

(25.21)

-

С?»’ (

В более подробной записи имеем собственные функции н их первые производные:

?! ^ — ?1 =—£иф4^ — С12?3^— £13?(>’*:

Ф2° = ^24а/ +^25^’/ + ^26» ¥2 , -= — С21У40 — 6’22?5> — ^23?0°;

9з(,) —Аа4о, 4 Ах-Л’Н-к1ь, — сЗцрі'* — с*!^0 —сірі' *; (25.26)

Т^> = *44и - ^4зТі + /г4в. 9*‘> = —

<Р5,,=^ь4и( І' ^'Л'і" I ^,'Х’ ?5 =—['гД ^

Чі'’—Я, и,4-/г6-;7,4-*бб> Тс*0— — Э? Ца°.

В далонейш^м введены следующие обозначения: для компонент векторов ии>: О1/1, ?У, !р‘;); для компонент векторов Д(?(л :

І(,л=т! Л ^л.=¥у»,

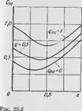
Рассмотрим пример численного определения частот пространственных ко - лебашні абсолютно гибкого стержня в потоке в зависимости от скорости пото­ка VI, (от <7яп и <?ю) при *іи=0,7, *'2к=0»4, а=90°. На рис. 25.2 приведены

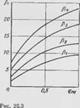Тудных значений аэродинамических сил (при счете принято <?1О=0,1 <?„0); на рис 25 4 — і рафики проекции ^«д - г (статических сил) в зависимости от Цпо: на рис. 25.3 - графики изменения первых четырех частот в зависимости от ско­рости потока (в зависимости от дпо)-