СИНХРОНИЗАЦИЯ МОД СОЛИТОННОГО ТИПА
Рассмотрим среду, в которой проявляется оптический эффект Керра, так что показатель преломления может быть записан в виде выражения (8.6.23), и предположим, что импульс света с однородным поперечным профилем интенсивности распространяется в среде вдоль направления г. На расстоянии г несущая волна импульса приобретает набег фазы, равный ср = со^ - $ьг или
ЮИпо±М12> (8.6.38)
С
Где I — интенсивность импульса. Теперь, поскольку I = /(£), мгновенная несущая частота импульса будет определяться выражением:
Щ = %Н£*)= (8.6.39)
Д* с дг
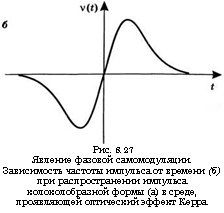
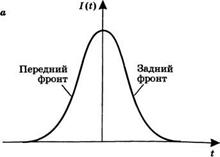
Поэтому несущая частота со = со(£) линейно зависит от отрицательной производной по времени распределения интенсивности света. Так, фаза ср = ср(*) для колокол образного импульса на рис. 8.27а будет промодулирована по времени интенсивностью пучка, и несущая частота будет изменяться со временем, как показано на рис. 8.276. Это явление называется фазовой самомодуляцией.
Следует отметить, что в области максимума импульса, т. е. в области, где поведение импульса во времени может быть описано параболической функцией, смещение частоты (или чирп), вызванное фазовой самомодуляцией, возрастает линейно от времени. Теперь предположим, что среда обладает отрицательной дисперсией групповой задержки. В этом случае импульс све*
та при распространении в такой среде (как показано в приложении Г) стремится приобрести мгновенный частотный чирп, линейно зависящий от времени.[43] Таким образом, оба эффекта стремятся перекрыть друг друга, и можно было бы ожидать, что при подходящих условиях фазовая самомодуляция могла бы полностью компенсировать эффект, обусловленный дисперсией всего импульса. Представленная интуитивная картина подтверждается подробными вычислениями, рассмотренными в работе [27]. Действительно, если импульс распространяется в среде с оптическим эффектом Керра и отрицательной дисперсией групповой скорости (такой как кремниевое оптоволокно при X > 1300 нм), распространение импульса с учетом фазовой самомодуля - ции описывается нелинейным волновым уравнением, которое допускает решение в виде импульса, распространяющегося без искажения. Оказывается, что временная зависимость соответствующего электрического поля для решений низшего порядка описывается функцией гиперболического секанса (или А(?) ос 8ес]1(£'/тр)], т - е., как показано выше, импульс является нечирпированным (без смещения частоты), и в результате взаимной компенсации фазовой самомодуляции и дисперсии групповой скорости весь импульс распространяется без искажения. Эти решения называются «одиночными» (солитонными) решениями нелинейного волнового уравнения, или солитонами. Одним из наиболее интересных свойств решения низшего порядка является соотношение между шириной импульса Дтр (на полувысоте) и пиковой мощностью импульса Рр [27]:
|
Рис. 8.27 Явление фазовой самомодуляции. Зависимость частоты импульса от времени (б) при распространении импульса колоколобразной формы (а) в среде, проявляющей оптический эффект Керра |
Р = уРр (8.6.40)
Где Ь2 =(й2Р/с/о)2)И1, у = п2(оь/сАеф и Аец— эффективная площадь пучка (Ас[/ = ли;2 для гауссова пучка с перетяжкой и>). Также можно показать, что у/2 — это просто нелинейный фазовый сдвиг на единицу длины и на единицу пиковой мощности (см. также (8.6.38)).
Теперь можно рассмотреть вопрос о том, может ли солитон образоваться в лазерном резонаторе с синхронизацией мод, содержащем среду, обладающую оптическим эффектом Керра и полностью отрицательной дисперсией групповой задержки. Ответом на этот вопрос является то, что солитонные решения являются неустойчивыми в резонаторе лазера с синхронизацией мод [28], но могут стать устойчивыми с помощью некоторого механизма нелинейных потерь, вызывающего амплитудную самомодуляцию (см. рис. 8.22 или 8.24). В этом случае, если пренебречь уширением импульса вследствие конечности ширины линии усиления, а также дисперсией высшего порядка, получается приблизительно устойчивое решение, которое эквивалентно распространению классического солитона в оптическом волокне с аномальной дисперсией. В частности, согласно (8.6.40) длительность импульса оказывается обратно пропорциональной энергии импульса Е (Е = 2,27РрАтр) и описывается выражением:
(8.е.41)
Где ф" — дисперсия групповой задержки за полный проход резонатора и 8 — нелинейный набег фазы за полный проход резонатора на единицу мощности в керровской среде. Набег фазы определяется как 5 = у 1К, где 1К — длина керровской среды. Из выражения (8.6.41), положив ф" = -200фс2, 6«10“6Вт-1 и Е « 50 нДж (что соответствует Тква лазеру с синхронизацией мод), получаем Дтр = 14 фс. В действительности солитоны наблюдались и в Тква лазере с синхронизацией мод, и в лазере на красителе (также с синхронизацией мод) при тщательной подстройке параметров лазера [29, 30]. В обоих случаях синхронизация мод использовалась в качестве механизма амплитудной самомодуляции, аналогичного тому, который возникает при керровской синхронизации мод или при совмещении медленного насыщающегося поглотителя с динамическим насыщением усиления. В обоих случаях могут быть получены очень короткие импульсы (10-20 фс) либо в чисто солитонном режиме, либо при КОМ' бинированном сочетании вместе с уширением импульса, обусловленным конечностью ширины линии усиления. Также важно отметить, что очень короткие импульсы синхронизации мод (-100 фс) были получены с помощью механизма солитонного типа даже с элементами, дающими намного более медленное «временное окно» полного усиления (например, полупроводниковые насыщающиеся поглотители с пикосекундным временем релаксации) [31]. В этом случае элемент для синхронизации мод только помогает стабилизировать солитон, в то время как длительность импульса, по существу, определяется выражением (8.6.41) для солитона.