АКТИВНАЯ СИНХРОНИЗАЦИЯ МОД
Существует три основных типа активной синхронизации мод, а именно:
■ синхронизация мод, которая осуществляется с помощью амплитудного модулятора (так называемая AM-синхронизация мод);
■ синхронизация мод, которая осуществляется с помощью фазового модулятора — ЧМ-синхронизация мод;
■ синхронизация мод, осуществляемая путем периодической модуляции усиления лазера с частотой повторения модулирующих импульсов, равной основной частоте резонатора Av = c/2L (синхронизация мод при синхронной накачке).
Здесь будет более подробно описана АМ-синхронизация мод, поскольку этот метод является наиболее часто встречающимся, тогда как ЧМ-синхро - низация будет рассмотрена более кратко. Синхронизация мод при синхронной накачке в силу того, что она используется реже всего, здесь обсуждаться не будет. Действительно, данный метод находит применение только в активных средах с временами релаксации, попадающими в наносекундный диапазон (особенно это касается активных сред на красителях), и для получения импульсов очень короткой длительности необходимо, чтобы частота повторения модулирующих импульсов накачки равнялась (с достаточно высокой точностью) основной частоте резонатора лазера. Поэтому на практике при использовании синхронизации мод и при синхронной накачке лазера на красителе достаточно сложно реализовать световые импульсы с длительностью менее 1 пс.
Для описания механизма АМ-синхронизации мод предположим, что в резонатор помещен управляемый внешним сигналом модулятор, который создает изменяющиеся во времени потери на частоте сот. Если сот ^ Асо, где Асо = 2яАу, и где Av является межмодовым расстоянием, то эти потери приведут просто к амплитудной модуляции электрического поля Ei(t) каждой моды резонатора:
El(t) = E0[ 1 — (5/2)(1 - cos comЈ)]cos (coz t + ф*), (8.6.17)
Где со, и фг — частота и фаза моды, а 5 представляет собой глубину модуляции. Это означает, что поле модулируется от значения Е0 до Е0( 1 - 8). Следует отметить, что в выражение (8.6.17) входит член 2Ј0(S/2)cos сomt х cos ((ott + ф;),
|
В модуляторе 2ут Световой импульс /(£) |
|
I |
|
T, |
|
Т |
|
Рис. 8.20 |
|
АМ-синхронизации мод во времени: А) условие стационарной генерации; б) световой импульс, приходящий до момента времени £т, соответствующего минимальным потерям; в) укорочение импульса, когда он приходит в момент времени £т. |
|
Представление процесса |
|
2Ут’ I А |
|
Потери в модуляторе |
|
T, |
|
Т |
|
А |
|
2у, Ik |
|
||
|
||
|
||
|
||
 |
||
|
||

Который можно записать в виде (E05/4){cos [(со* + com)f + ф*] + cos [(со* - соm)t + + ф*]}. Таким образом, поле£*(£) на самом деле содержит две компоненты, осциллирующие на частотах со* ± сот (боковые полосы модуляции). Если теперь сот = Асо, то эти боковые полосы совпадут с частотами соседних мод резонатора. Следовательно, члены, содержащие выражения для этих боковых полос, войдут в два уравнения для полей соседних мод резонатора. Поэтому уравнения мод резонатора становятся связанными, т. е. образуют систему в том смысле, что уравнение для поля одной моды резонатора будет содержать два члена, возникающих при модуляции двух соседних мод [16]. Можно показать, что при этом механизме синхронизации, если модулятор расположен очень близко к одному из зеркал, фазы мод будут синхронизированы в соответствии с выражением (8.6.1).
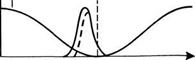
Принцип действия АМ-синхронизации мод, возможно, легче понять, если рассматривать ее во временном, а не в частотном представлении. На рис. 8.20а показана временная зависимость потерь 2у в резонаторе за полный проход,[40] которые модулируются с периодом Т = 2п/ыт. Будем считать, что модулятор расположен вблизи одного из зеркал резонатора (см. рис. 8.19а). Если теперь сот = Асо, то период модуляции Т будет равен времени полного прохода резонатора, и в этом случае прохождение световых импульсов (функция I(t) на рис. 8.20а)) через модулятор в момент времени tm при минимальных потерях будет соответствовать условию стационарной генерации. Действительно, импульс, который проходит через модулятор в момент времени tm при минимальных потерях, будет снова возвращаться в модулятор через интервал времени 2L/c, когда потери вновь станут минимальными. С другой стороны, если предположить, что импульс изначально проходит через модулятор в момент времени, скажем, чуть раньше tm (показан сплошной кривой на
рис. 8.206), то благодаря изменяющимся во времени потерям модулятора передний фронт импульса будет испытывать меньшие потери, чем задний фронт. Следовательно, после прохождения через модулятор светового импульса, показанного штриховой линией на рис. 8.206, момент времени, в который наблюдается пик импульса, сдвигается таким образом, что при следующем прохождении пик окажется ближе к Ьт. Это показывает, что случай на рис. 8.20а соответствует устойчивой синхронизации мод. Действительно, в этом случае за время изменения величины потерь 2ут(£) длительность импульса будет укорачиваться каждый раз после его прохождения через модулятор, поскольку и передний, и задний фронты импульса будут претерпевать некоторое ослабление, в отличие от области пика импульса, см. рис. 8.20в. Если рассматривать только этот механизм развития, то длительность импульса в конечном итоге должна устремиться к нулю при очень большом числе проходов через модулятор. Однако этому препятствует ограниченная ширина спектра усиливающей среды. Действительно, когда импульс укорачивается, его спектр, в конечном итоге, уширяется до ширины линии генерации лазерной среды. Таким образом, крылья спектрального распределения импульса больше не могут усиливаться, что накладывает основные ограничения на спектральную ширину импульса, а следовательно, и на его длительность.
В зависимости от того, однородно или неоднородно уширенной является лазерная линия, влияние ограниченности спектральной полосы активной среды на длительность импульса в режиме стационарной генерации может быть различной. В случае неоднородно уширенной линии и при значительном превышении накачки над порогом, ширина линии генерации Ауь стремится занять всю ширину линии усиления Ду£. Действительно, если описывать данный процесс в представлении частотной области, то основной функцией модулятора является синхронизация этих уже генерирующих мод. При выполнении условия синхронизма сот = Асо, а также в случае, когда АМ-модулятор помещен на одном из концов резонатора, условие (8.6.1) синхронизации фаз становится очевидным. Теперь, предполагая для простоты, что амплитуды мод имеют гауссово распределение, из выражения (8.6.12) получаем:
Лтр = 0,441/Ауо. (8.6.18)
С другой стороны, в случае однородно уширенной линии спектр генерации стремится сосредоточиться в узкой области около центральной частоты у0, что обусловлено эффектом пространственного выжигания дырок, см. раздел 7.7. Таким образом, предполагая, что лазер изначально не синхронизован, следовало бы ожидать, что импульсы спонтанного излучения (см. рис. 8.15) будут значительно более уширены, чем величина 1/Ау0, где Ау0 — ширина линии усиления. В этом случае механизм, продемонстрированный на рис. 8.20в, является действительно эффективным при уменьшении длительности импульса (т. е. при уширении его спектра). Однако этому уменьшению противодействует уширение длительности импульса, которое имеет место, когда импульс проходит через активную среду, и которое связано с уменьшением ширины линии генерации импульса. Теория активной синхронизации мод для случая однородно уширенной линии была достаточно детально и просто описана в работе Куйзенга и Сигмана[17] и позднее представлена в более общем виде в работе Хауса [18]. В данном разделе будут рассмотрены лишь наиболее значимые результаты, а более подробное описание читатель может найти в приложении Г. При обычных условиях профиль интенсивности может быть описан гауссовой функцией, ширина Ахр которой на половине высоты максимума приближенно задается выражением:
&тр = 0,45/(утДу0)1/2, (8.6.19)
Где ут — частота модуляции (ут = сот/2к = с/2Ь для синхронизации мод в режиме второй гармоники). Если сравнить выражения для длительностей импульсов в случае неоднородно уширенной (8.6.18) и однородно уширенной (8.6.19) линий усиления при одном и том же значении ширины лазерной линии (т. е. при Лу5 = Ду0), то нетрудно видеть, что поскольку (уш/Ду0) 1, имеем (Атр)однородн » (Лунеоднород„- Можно, таким образом, отметить, что ме - ханизм сужения длительности импульса, изображенный на рис. 8.20в, не играет сколько-нибудь существенной роли в случае неоднородно уширенной линии, хотя, очевидно, действует и в этом случае. Действительно, длительность импульса в данном случае определяется обратной шириной линии даже без выполнения условия синхронизации мод. И основная роль модулятора здесь состоит в осуществлении такого синхронизма между модами, на которых происходит генерация, при которой световые импульсы (см. рис. 8.15) проходят через модулятор в те моменты времени, когда потери минимальны (рис. 8.20а).
Пример 8.7.AM-синхронизация мод при использовании непрерывного аргонового лазера и Nd:YAG лазера. Вначале рассмотрим аргоновый лазер, работающий в режиме синхронизации мод (длина волны зеленого перехода X = 514,5 нм). Линия данного перехода является доплеровски уширенной с шириной Ау5=3,5ГГц. Из выражения (8.6.18) находим Атр = 126 пс. Теперь рассмотрим Nd:YAG лазер, генерирующий на длине волны X = 1,064 мкм. Уширение линии данного перехода связано с фонон - ными процессами, происходящими в кристаллической решетке, и ширина линии здесь составляет Av0 = 4,3 см-1 = 129 ГГц при температуре Т = 300 К. Возьмем резонатор с оптической длиной Le= 1,5 м и рассмотрим случай, когда AM-модулятор помещен на одном из концов резонатора (рис. 8.19а). Таким образом, получаем vm = c/2Le = 100 МГц, и из выражения (8.6.19) находим Атр = 125 пс. Следует отметить, что длительности импульсов Атр в рассмотренных случаях однородно и неоднородно уширенных линий практически не отличаются, несмотря на то что ширина линии в Nd: YAG лазере почти в 30 раз больше, чем тот же параметр в аргоновом лазере.
Для описания механизма ЧМ-синхронизации мод предположим, что модулятор, показатель преломления п которого модулируется по синусоидальному закону с частотой сот, помещен на одном из концов резонатора. Следовательно, в этом случае любая заданная мода будет испытывать изменяю*
Щийся во времени сдвиг фазы, определяемый как п» (р = (2пЬ'/Х) • n(t), где!/ — длина модулятора. Такие промодулированные по фазе моды будут демонстрировать боковые полосы (см. выражение (7.10.5)), чьи частоты при условии сот = Асо будут совпадать с частотами соседних мод. Таким об-
|
UUUUL |
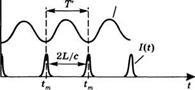
![]() Разом, такие моды будут снова связанными и их рис. &.21 1
Разом, такие моды будут снова связанными и их рис. &.21 1
Фазы синхронизованы [161, хотя синхронизации ЧМ-синхронизация мод.
~ ^ ч Временная зависимость
Между ними будут отличаться от условия (8.6.1). показателя преломления
В представлении временной области ЧМ-синхро - модулятора п и
Интенсивности I выходного низацию мод можно описать так, как это пока - излучения лазера
Зано на рис. 8.21. Заметим, что в этом случае имеются два устойчивых состояния синхронизации мод, при которых световой импульс проходит через модулятор либо при каждом минимуме функции n(t) (импульсы, изображенные сплошными линиями), либо при каждом максимуме (импульсы, изображенные штриховыми линиями).
Для понимания этого механизма необходимо вначале отметить, что, поскольку оптическая длина модулятора равна L'e = n(t)L этот тип модулятора производит модуляцию эффективной длины резонатора Le. Таким образом, действие модулятора эквивалентно тому, как если бы в резонаторе без модулятора заставили колебаться одно из зеркал с частотой сот. В соответствии с ситуацией, изображенной на рис. 8.21, импульсы в режиме синхронизации мод стремятся попасть на зеркало в тот момент времени, когда оно находится в одном из своих крайних положений (т. е. когда оно находится в покое). Следует отметить, что после отражения от движущегося зеркала фаза импульса будет изменяться по закону, близкому к параболе, либо с положительным знаком (для импульсов, изображенных сплошной линией), либо с отрицательным знаком (для импульсов, изображенных штриховой линией), и спектр таких импульсов будет слегка уширен. В конечном итоге модуляция фазы импульса, а, следовательно, и его длительность достигнут такого состояния, когда спектральное уширение, связанное с каждым последующим отражением от движущегося зеркала, будет компенсироваться сужением спектра в результате прохождения импульса через усилитель. Для понимания данного процесса (т. е. попадания импульса на движущееся зеркало в момент, когда оно находится уже почти в неподвижном состоянии) можно провести анализ устойчивости системы. Однако такой анализ является достаточно сложным, и в силу некоторых ограничений, присущих данному типу синхронизации мод, он рассматриваться здесь не будет. Действительно, ЧМ-синхронизация мод используется на практике не так часто. Это связано с двумя основными причинами:
■ импульсы являются частотно модулированными;
■ синхронизация такого типа обладает некоторой нестабильностью и, в частности, это зачастую приводит к перескокам между двумя состояниями, показанными на рис. 8.21.
В мощных импульсных лазерах (с большим коэффициентом усиления) АМ-синхронизация мод, как правило, реализуется с помощью амплитудного модулятора, основанного на ячейке Поккельса. Возможная конфигурация
Модулятора на ячейке Поккельса изображена на рис. 8.5а. Прикладываемое к ячейке напряжение модулируется по синусоидальному закону от нуля до доли четвертьволнового напряжения. При непрерывной накачке и в лазерак с небольшим усилением АМ-синхронизация обычно осуществляется акустооп - тическим модулятором, поскольку потери, вносимые этим модулятором в ре* зонатор, меньше, чем модулятором на ячейке Поккельса. Однако акустоопти - ческий модулятор, используемый для синхронизации мод, значительно отличается от того, который применяется при модуляции добротности (см. рис. 8.7), поскольку грань, к которой прикреплен преобразователь, и противоположная грань оптического блока вырезаны параллельно друг другу. Звуковая волна, возбуждаемая преобразователем, теперь отражается назад противоположной гранью блока. Таким образом, если длина оптического блока равна целому числу полуволн звуковой волны, то возникают стоячие звуковые волны. Поскольку амплитуда стоячей волны модулируется во времени по синусоидальному закону, то так же будут модулироваться и дифракционные потери. Можно показать, что если звуковая волна осциллирует на частоте со, то дифракционные потери будут промодулированы с частотой 2со. Рассмотрим стоячую звуковую волну вида 5 = 50 (совсо^Хвіп^г). Дифракционные потери в модуляторе достигают максимума в те моменты времени, когда имеют место максимумы амплитуды стоячей волны, которые достигаются дважды за период колебаний (а именно, при і = Ои при £ = к/со). Таким образом, потери модулируются с частотой 2со, и синхронизация мод в режиме основной частоты (см. рис. 8.19а) происходит при выполнении следующих двух условий:
■ если модулятор расположен как можно ближе к одному из зеркал резонатора;
■ если частота модуляции 2у равна величине (с/2Ь) и преобразователь возбуждается с частотой V, равной с/41, (например, V = 50 МГц при Ь = 1,5 м). В случае ЧМ-синхронизации мод (как для импульсных, так и для непрерывных лазеров), как правило, применяется электрооптический фазовый модулятор на основе ячейки Поккельса. Здесь одна из двух осей, например х, вдоль которой наводится двулучепреломление (см. рис. 8.56), ориентирована вдоль оси поляризации. Таким образом, пучок не претерпевает поворот плоскости поляризации при прохождении через ячейку Поккельса, но при этом имеет место фазовый сдвиг, определяемый как ф = (2л1//к)пх, где I/ — длина ячейки Поккельса, и пх — показатель преломления для поляризации вдоль направления х. Если теперь промодулировать напряжение на ячейке Поккельса сигналом синусоидальной формы, то показатель преломления пх, в силу эффекта Поккельса, будет также промодулирован по синусоидальному закону, и фаза пучка в этом случае будет изменяться таким же образом.