ДИНАМИЧЕСКИ И МЕХАНИЧЕСКИ УСТОЙЧИВЫЕ РЕЗОНАТОРЫ
Очень важной задачей, возникающей в устойчивых резонаторах, является получение сравнимых по величине размеров поперечного сечения пучка и активной среды. Действительно, рассматривая для простоты симметричный двухзеркальный резонатор, из соотношения (5.5.10) можно видеть, что для того, чтобы существенно увеличить поперечные размеры пучка внутри резонатора сверх величины, характерной для конфокального резонатора, необходимо выбрать резонатор с параметрами более близкими к g = ±1 (квазип - лоский или квазиконцентрический резонатор). Тогда он окажется слишком близко к границе устойчивости и, вообще говоря, будет весьма чувствителен к любым возмущениям, например связанным с флуктуациями мощности накачки. Рассмотрим теперь конструкцию лазерного резонатора, обеспечивающую большие поперечные размеры пучка внутри активной среды и при этом практически нечувствительную к возмущениям резонатора — либо из - за флуктуаций мощности накачки, либо из-за изменений углов наклона зеркал (динамически и механически устойчивый резонатор) [7].
Вначале рассмотрим лазерный резонатор общего вида, состоящий из двух сферических зеркал с радиусами кривизны Rx и R2 и содержащий активную среду, тепловое влияние излучения накачки на которую может быть смоделировано тонкой линзой с оптической силой 1 //, пропорциональной мощности накачки (рис. 5.14а). Такая модель особенно хорошо применима для твердотельных лазеров. Однако некоторые из обсуждаемых ниже идей можно также использовать при рассмотрении более сложных возмущений активных сред вследствие накачки, имеющих место в газах.
Первое ограничение на конструкцию лазерного резонатора на рис. 5.14а получается из условия, что размер поперечного сечения пучка, или пятна,
|
|
![]()
![]()
|
2а |
![]() А, Б,
А, Б,
Сх Dx
L
Рис. 5.14
А) Двухзеркальный сферический резонатор общего вида, включающий линзу с фокусным расстоянием /, которая моделирует тепловую линзу в активной среде, б) Обобщение резонатора из (а), с матричными элементами Ах, ВХУСХ и Бх для одного прохода, учитывающими матрицу тепловой линзы
IVа в активной среде не должен зависеть от оптической силы линзы. Таким
|
Образом |
![]()
|
(5.5.30) |
![]() Dwa/d(l/f) = 0.
Dwa/d(l/f) = 0.
Резонатор, который удовлетворяет этому условию, часто называют динамически устойчивым. Второе ограничение может быть получено из условия, что размер пятна и? а должен быть сравним с радиусом а активной среды. Для того чтобы избежать внесения излишних дифракционных потерь за счет ограничения пучка этой апертурой, можно, например, потребовать выполнения соотношения (см. [8])
|
(5.5.31) |
![]() 2а = nwa.
2а = nwa.
При заданных значениях величин а и 1/f соотношения (5.5.30) и (5.5.31) представляют собой пару уравнений для определения параметров резонатора #!, Е2, Ьх и L2.
Теперь зададимся вопросом, является ли динамически устойчивая ситуация в резонаторе на рис. 5.14а реально осуществимой. Чтобы дать на него ответ, рассмотрим показанную на рис. 5.15 зависимость величины и? а в рассматриваемом резонаторе от оптической силы 1 /f при заданных значениях других параметров резонатора. Из этого рисунка можно сделать следующие общие выводы:
■ при изменении оптической силы существуют две динамически устойчивых точки, удовлетворяющих соотношению (5.5.30);
|
Зависимости размера пятна и>а в активной среде и суммарной чувствительности к угловой расстройке от оптической |
|
Рис. 5.15 |
|
Силы І/f для резонатора |
|
На рис. 5.14а |
|
|
 |
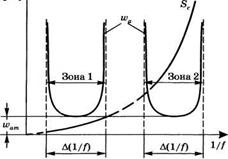
■ обе точки отвечают минимуму зависимости и)а от 1//, причем величи wam — одна и та же для обеих точек;
■ минимумы принадлежат двум зонам устойчивости, причем размеры у я - тен возрастают до бесконечности на границах каждой из зон;
■ ширина Д( 1 /f) одинакова для обеих зон; она связана с минимальным размером пятна фундаментальным соотношением
Не зависящим от величин других параметров резонатора.
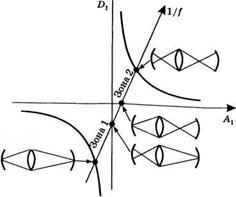
Существование двух зон устойчивости можно описать в общем виде, если обратиться к рис. 5.146 (см. также рис. 5.8г), который представляет собой обобщение рис. 5.14а и где элементы Аг, Bl9 Сх и^ матрицы для одного прохода оказываются линейными функциями величины 1 //. Из соотношений (5.4.6) и (5.5.5) следует, что в терминах матричных элементов условие устойчивости может быть записано в виде О ^ 1. Это условие устойчи*
Вости показано на рис. 5.16, где по горизонтальным и вертикальным осям представлены соответственно величины Ах и Dt. Поскольку Ах и Dx являются линейными функциями 1//, то график зависимостй величин Ах от соответствующих величин Dl9 получаемый при изменении параметра 1//, будет иметь в плоскости Al9 Dx вид прямой линии (см. рис. 5.16). Эта линия пересекает границы устойчивости в четырех точках, определяющих две зоны устойчивости. Конфигурации лазерных пучков, отвечающие этим граничным точкам, изображенные в приближении геометрической оптики, также пока* заны на рисунке.
Разобравшись с происхождением двух зон устойчивости, отметим, что оптическая сила линзы, наведенной накачкой в стержне, может быть представлена в виде [9]:
1= k р
F па2 а' (5.5.33)
ГДе Ра мощность накачки, поглощенная в стержне, а к — характерная для данного материала константа. Если выражение (5.5.33) для 1/f подставить
|
|
|
Рис. 5.16 Диаграмма устойчивости для обобщенного резонатора, изображенного на рис. 5.146. Показаны также представленные на рис. 5.15 две зоны устойчивости и соответствующие границам этих зон изображения хода лучей в резонаторе в приближении геометрической оптики |
В (5.5.32) и в получившемся соотношении, в соответствии с (5.5.31), положить (wam/a) = (2/я), то нетрудно увидеть, что ширина диапазона приемлемой поглощенной мощности АРа, отвечающей каждой зоне устойчивости, постоянна для данного лазерного материала (например, АРа = 10 Вт для NdrYAG лазера, накачиваемого излучением диодного лазера).
Из предыдущего рассуждения создается впечатление, что оптические свойства резонаторов в двух зонах устойчивости одинаковы. Однако при рассмотрении устойчивости лазерного резонатора по отношению к угловой расстройке выявляются сильные различия между этими зонами. Вначале определим чувствительности к угловой расстройке Sx и S2 для зеркал 1 и 2 в соответствии с соотношениями S1 = и S2 = $rc2/M>a502,
Где, например, для зеркала 1 5гс1 обозначает смещение центра пучка в лазерном стержне за счет изменения наклона 80! зеркала 1, и аналогично — для зеркала 2. Определим теперь полную чувствительность обоих зеркал к угловой расстройке как Sc =[Sf +Sf]1/2. Зависимость этой полной чувствительности от оптической силы линзы также показана на рис. 5.15. Видно, что в одной из двух зон, называемой далее зоной 1, чувствительность резонатора к угловой расстройке (разъюстировке) зеркал гораздо меньше, чем в другой, называемой далее зоной 2. Причину меньшей чувствительности к разъюстировке в зоне 1 можно понять, если обратить внимание на то, что размеры пятен на зеркалах в зоне 1 гораздо меньше, чем в зоне 2. Действительно, в приближении геометрической оптики одна из двух границ устойчивости зоны 1 отвечает фокусировке пучка на поверхности обоих зеркал (см. рис. 5.16). Таким образом, вблизи этой границы размер пятна на зеркале wm очень мал, так что расходимость пучка 0 « 0d = fk/nwm достаточно велика. Следовательно, изменение наклона зеркала, необходимое для поворота оси пучка на угол, сравнимый по величине с расходимостью, также должно быть велико.
В заключение можно сказать, что изображенный на рис. 5.146 обобщенный резонатор, содержащий элемент с изменяемыми параметрами, такой как, например, наведенная тепловая линза в активном элементе, может быть реализован в виде динамически и механически устойчивой конфигурации. Параметры этого резонатора должны соответствовать зоне 1 и удовлетворять условиям (5.5.30), (5.5.31). На практике, вместо того, чтобы обеспечивать выполнение условия (5.5.30), можно выбрать параметры резонатора так, чтобы он находился в центре зоны 1. Если считать, что расстояние Ll9 показанное на рис. 5.14а, является изменяемым параметром, то его величину можно выбрать средней между граничными значениями Ц и Ц для зоны 1. Из представления в приближении геометрической оптики, показанного на рис. 5.16, находим, что Ц и Ц должны удовлетворять соответствующим соотношениям L[1 + Ь2г =f ~l иЩ-Ri )_1 + L2l =f~l9 где расстояние L2 также показано на рис. 5.14a. Будучи рассчитан для определенного фокусного расстояния f и, следовательно, для заданной поглощенной мощности Ра9 резонатор будет устойчиво работать в некотором диапазоне мощностей АРа, величина которого для данной активной среды не зависит от параметров резонатора.