ГАУССОВЫ ПУЧКИ И ЗАКОН АВСИ
Распространение гауссова пучка через некоторую среду, которая характеризуется АВС£>-матрицей, описывается соотношением (4.7.3) [8]. При заданной АВС2)-матрице результат зависит только от комплексных параметров ид пучков соответственно на входе и на выходе, так что величина<7, при данной величине непосредственно определяется через матричные эле
Менты с помощью соотношения (4.7.4). Таким образом, это соотношение является единственным, которое необходимо для расчета параметров пучка на выходе. Физический смысл соотношения (4.7.4) легко понять, сравнивая его с соотношением (4.2.19), которое показывает, каким образом оптическая система преобразует радиус кривизны волнового фронта сферической волны. Действительно, как было показано ранее, гауссов пучок можно формально рассматривать как сферическую волну с комплексным радиусом кривизны волнового фронта, а соотношение (4.7.4) показывает, что этот комплексный параметр преобразуется точно так же, как и радиус кривизны волнового фронта сферической волны. Соотношение (4.7.4) — закон АВСБ распространения гауссовых пучков — оказывается, таким образом, очень важным законом. Его польза уже была продемонстрирована в разделе 4.7.2 на примере свободного распространения волны. В данном разделе важность этого закона будет показана на более сложных примерах.
-1- =_1 + _к (4.7.22)
42 f Ъ
Используя соотношение (4.7.8) для того, чтобы записать выражения как для 1/<7х, так и Для 1/(72» можно отдельно приравнять действительную и мнимую части формулы (4.7.22), чтобы получить следующие соотношения | между размерами пятна и радиусами кривизны волнового фронта перед и
1 за линзой:
Ьи2==ьи 1, (4.7.23а)
= (4.7.236)
В.2 ^1 /
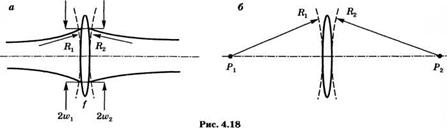
Теперь, обратясь к рис. 4.18, можно обсудить физический смысл соотношений (4.7.23). Рассматривая вначале (4.7.23а), можно сразу заметить, что его физический смысл очевиден, поскольку в случае тонкой линзы распределения амплитуд напряженности поля непосредственно перед и сразу же за линзой должны быть одинаковыми; т. е. размер пятна не может измениться скачком (см. рис. 4.18а). Чтобы понять смысл соотношения (4.7.236), рассмотрим вначале распространение обычной сферической волны через ту же самую линзу (рис. 4.186). Здесь сферическая волна, испускаемая точечным источником Ръ отображается линзой в точку Р2. Радиусы кривизны и 112 волнового фронта непосредственно перед и сразу же за линзой должны быть связаны соотношением (4.2.20). Таким образом, можно видеть, что сферическая линза преобразует радиус кривизны #1 фронта падающей волны в радиус кривизны Л2 фронта прошедшей волны в соответствии с (4.2.20). Поскольку естественно предполагать, что такое преобразование должно происходить независимо от поперечного распределения амплитуды напряженности поля, то следует ожидать, что (4.2.20) должно выполняться также и для гауссовых пучков, что в действительности и показывает соотношение (4.7.236).
|
Прохождение через тонкую линзу: а) гауссова пучка; б) сферической волны. |
Пример 4.6. Фокусировка гауссова пучка тонкой линзой. Рассмотрим теперь гауссов пучок с размером пятна ш01 и плоским фронтом, падающий на линзу с фокусным расстоянием / (т. е. перетяжка пучка находится в плоскости линзы). Определим положение перетяжки пучка и соответствующий ей размер пятна ьи02 за линзой. Согласно (4.2.4) и (4.2.6), матрица
|
Преобразования для линзы с фокусным расстоянием /, за которой расположен слой свободного пространства толщиной 2, имеет вид |
|
1-2// 2 -1 // 1 |
|
(4.7.24) |
|
(х2+у2) (4.7.30) 2q ’ |
|
V2у W |
|
Х exp— jk |
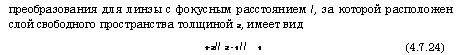 |
|
|
|
|
|