РАСПРОСТРАНЕНИЕ В СВОБОДНОМ ПРОСТРАНСТВЕ
Рассмотрим распространение гауссова пучка вида (4.7.1) вдоль положительного направления оси г при отсутствии какой бы то ни было ограничивающей апертуры в направлении х или у (т. е. в свободном пространстве). Из соотношения (4.7.4) сА = 1)=1иБ = г получаем:
Q = qi + z. (4.7.11)
Полагая, что при zx = 0 R = со, можно записать:
A/qi) = ~jfr/nw2), (4.7.12)
Где w0 — размер пятна при гх = 0. Запишем теперь соотношение (4.7.11) в
Виде (1/(7)= 1 /(<?! +гЛ подставим 1/q из (4.7.8) и 1 /qx из (4.7.12), а затем
Выделим действительную и мнимую части полученного соотношения. После некоторых несложных алгебраических преобразований получим выражения для размера пятна w и радиуса кривизны R волнового фронта в виде:
2"
|
(4.7.13a) |
![]() Xz
Xz
|
1 + |
![]()
|
KW; |
![]() W2(z) = wf
W2(z) = wf
Oj
|
>2 |
|
KWfi Tz |
|
R(z) = z |
|
1 + |
|
|
Используя соотношения (4.7.3) и (4.7.12), можно также записать:
|
И(х9 у у z) = |
|
1 - j(Xz/nw2) |
|
X2 + I!2 Ехр |
|
|
Комплексный множитель в первой скобке выражения (4.7.14) может быть теперь выражен в виде амплитудного и фазового сомножителей. Используя также соотношение (4.7.8) для (1 /#), получим выражение для напряженности поля в виде:
IVn X2 + и2 х2 + и2
И(х, у,z) =— exp-------- т^-ехр-jk - * ехр;ф, (4.7.15а)
2
|
IVе |
![]()
|
U) |
![]() R
R
/ ~ Л
Кг
|
О у |
![]() Пи;;
Пи;;
Выражение (4.7.15а), вместе с выражениями для w(z), R(z) и ф(г), задаваема ми соотношениями (4.7.13) и (4.7.156), полностью решают рассматривав мую задачу. Из соотношений (4.7.13) и (4.7.156) видно, что величины w> ft и ф (и, следовательно, распределение напряженности электрического поля) зависят только от параметра w0 (при заданных А, и г). Это легко понять, если обратить внимание на то, что если величина w0 определена, то тем самым задано распределение напряженности электрического поля в плоскости гх = 0. Действительно, известна амплитуда напряженности, поскольку ее распределение задается гауссовой функцией с размером пятна w0, и ее фаза, поскольку предполагается, что R = оо при 2 = 0. Если известно распределение напряженности электрического поля в плоскости гх = 0, то и соответствующее распределение при г > 0 однозначно определено и может быть рассчитано, например с помощью интеграла Френеля-Кирхгофа (4.6.8). Снова используя соотношение (4.7.11), можно показать, что выражения (4.7.13) справедливы также и при отрицательных значениях г9 т. е. при распространении вперед не только от плоскости гх = 0. Отметим, что если ввести параметр
2R=nw$/X9 (4.7.16)
Где величину 2r называют длиной Рэлея (смысл этого параметра будет обсуждаться ниже), то выражения (4.7.13) и (4.7.156) могут быть представлены в более наглядном виде, а именно:
U>2(2)=w2[l+(z/zK)2], (4.7.17а)
Д(2) = 2[1+(2д/2)2], (4.7.176)
Ф(г) = tan-1 (г/2д). (4.7.17в)
Выражения (4.7.15а) и (4.7.17) представляют собой конечную цель проводимых расчетов. Видно, что функция и(х9 у9 г) является произведением амплитудного, (w0/w) • ехр-[(х2 + у2)/и>29 и фазовых — поперечного, ехр - - jk[(x2 + y2)/2R]9 и продольного, ехр £ф, — сомножителей. Физический смысл этих сомножителей обсудим более детально в последующих разделах.
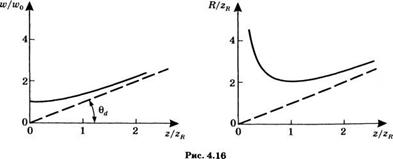
А б
|
А) Нормированный размер пятна и>. б) Нормированный радиус кривизны волнового фронта Я в зависимости от нормированной координаты г |
Амплитудный сомножитель в (4.7.15а) показывает, что пучок по мере распространения (как при г > О, так и при г < 0) сохраняет свою гауссову форму, но размер его пятна изменяется в соответствии с соотношением (4.7.17а). Таким образом, величина ю2(г) может быть записана в виде суммы ц>о и (Х2/пю0)2 — слагаемого, обусловленного дифракцией. Зависимость нормированного размера пятна и>/и>0 от нормированной координаты г/2д при г > 0 показана сплошной линией на рис. 4.16а. При г < 0 размер пятна можно легко получить из этого же графика, поскольку ю(г) — четная функция 2, т. е. симметрична относительно оси ординат. Таким образом, размер пятна минимален при 2 = 0 (поэтому эта координата называется перетяжкой пучка); при 2 = 2п имеем ю - [2ю0. Таким образом, длина Рэлея — это расстояние от перетяжки пучка до того места на его оси, где пятно увеличивается в^2 раз. При 2 —^ оо (т. е. при 2 2К) можно записать:
IV « и)02/2ц = 'К2/пи>0. (4.7.18)
Зависимость (4.7.18) также представлена на рис. 4.17а (пунктирная линия). При больших 2 величина IV возрастает линейно с г; следовательно, можно определить расходимость пучка за счет дифракции как отношение 0а = IV/2. Получаем
0а = Х/пи! 0. (4.7.19)
Физическую причину присутствия множителя и>0/и> в амплитудном сомножителе выражения (4.7.15а) легко понять, если обратить внимание на то, что поскольку потери в среде считаются пренебрежимо малыми, то полная мощность излучения в любой плоскости 2 должна быть одной и той же. Это означает, что интеграл Д| и 2с1хс1у не должен зависеть от 2. Присутствие множителя и>0/и>(2) обеспечивает выполнение этого условия. Действительно, используя (4.7.15а), можно записать:
+00 +00
Дойр (1хс1у = (и)1 /2) |ехр(-^2)с^ |ехр(-т12)с/т], (4.7.20)
—00 —00
Где = &х/ и>иг = [2у/и). Видно, что ^и2с1хс1у не зависит от 2.
Обратимся теперь к поперечному фазовому сомножителю (4.7.15а). В соответствии с описанием, приведенным в разделе 4.7.1, он показывает, что при распространении в области 2 > 0 пучок имеет приблизительно сферический волновой фронт с радиусом кривизны Я. Зависимость нормированного радиуса кривизны Я/2 я от нормированной координаты 2/2п при 2 > 0 изображена на рис. 4.166. При 2 < 0 радиус кривизны легко определить из этого же рисунка, поскольку Щ2) — нечетная функция г, т. е. антисимметрична относительно оси ординат. Видно, что # —» оо при 2 = 0и принимает минимальное
Рис. 4.17 Профиль пучка (сплошные линии) и поверхности одинаковой фазы (пунктирные линии) для гауссовой моды низшего порядка (Т2£М00)
/ /
Значение при г = гк. При г^> гв имеем Я « г, а линия И = г показана пунктиром на рис. 4.166. Таким образом, волновой фронт является плоским при г = 0, а на больших расстояниях от перетяжки радиус его кривизны возрас тает линейно с 2, как у сферической волны.
Наконец, рассмотрим продольный фазовый сомножитель в выражении (4.7.15а). Используя (4.6.4) и (4.7.156), видим, что помимо фазы - кг плоской волны гауссов пучок имеет дополнительный вклад ф(г), изменяющийся от -(л/2) до (л/2) при распространении пучка из области г —гЕ в область г
Результаты, приведенные на рис. 4.16, объединены на рис. 4.17, где сплошными линиями показаны размеры пятна 2и>(г) (профиль пучка), а пунктирными — волновые фронты (поверхности одинаковой фазы). Поперечное сечение пучка имеет минимальные размеры в виде перетяжки при 2 = 0; соответствующий размер пятна ю0 обычно называют размером пятна в перетяжке пучка. Отметим, в соответствии с используемым соглашением о знаке кривизны волнового фронта, что поскольку Я > 0 при г > 0 и Я < 0 при
2 < 0, то центр кривизны находится слева от волнового фронта при г > 0 и справа от него при г < 0.