МОДА НИЗШЕГО ПОРЯДКА
Рассмотрим некоторую обобщенную оптическую систему, характеризуемую соответствующей ABCD-матрицей (см. рис. 4.14). Зададимся вопросом, существует ли такое решение уравнения (4.6.9), которое сохраняет свой функциональный вид по мере распространения волны в пространстве? Другими словами, существует ли собственное решение уравнения (4.6.9)? Ответ легко получить, если предположить, что в плоскости zl = 0 нет ограничивающей апертуры, так что двойное интегрирование в (4.6.9) можно проводить в пределах от - go до +оо как для х, так и для у координат. В этом случае путем прямой подстановки в уравнение (4.6.9) можно показать, что функция
И(х, у, г) ос exp - jk[(x2 + y2)/2q], (4.7.1)
|
Aqx +В Cqx + D |
|
<7 = |
|
X2 Л-у2 2q |
|
Ё ос ехр - jk |
|
(4.7.5) |
|
Z + |
|
Рассмотрим сферическую волну с центром в точке с координатами х1=у1 = = гх = 0. Напряженность электрического поля этой волны в точке Р(х, у9 г) может быть выражена в виде Ё ос [exp - jkR] / R, где R — радиус кривизны ее волнового фронта. В параксиальном приближении, следуя той же аргументации, что и при выводе соотношения (4.6.6), запишем: |
|
X2 +у2 2R |
|
R = 2 - ь |
|
Поле сферической волны преобразуется при этом к виду: Ё ОС exp - jk |
|
Х2+у2 2R |
|
2-У |
|
~ _j_ j.2 Е(х, у, 2) ОС ехр-------- х exp - jk Wz |
|
X2 4-у2 2R |
|
2 + |
|
Сравнение выражений (4.7.7) и (4.7.5) показывает, что гауссов пучок можно рассматривать как сферическую волну с комплексным радиусом кривизны волнового фронта, равным q. Для того чтобы выяснить физический смысл этого комплексного параметра пучка, выделим действительную и мнимую части величины l/q, т. е. запишем: 1 _ 1 . X (4.7.8) |
|
Q R ^nw2* Подстановка выражения (4.7.8) в (4.7.5) дает: |
|
|
|
|
|
|
 |
|
|
|
|
|
 |
|
 |
|
|
|
 |
|
|
|
 |
|
 |
|
|
|
|
|
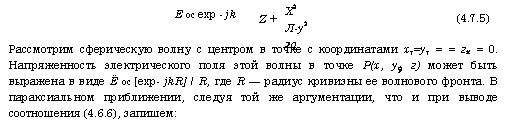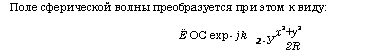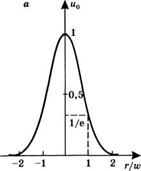Профиль напряженности электрического поля для гауссовых мод: а) низшего порядка; б) первого порядка.
Теперь можно обсудить физический смысл параметров ю и Л, входящих в формулу (4.7.8).
Для того чтобы понять смысл параметра ю, рассмотрим представленную на рис. 4.15а зависимость амплитудного множителя в правой части соотношения (4.7.9), т. е. и0 = ехр-[(х2 + у2)/и>2, от величины г/ю, где г = [х2 + у2]1/2 — радиальная координата точки внутри пучка. Видно, что амплитудный множитель достигает максимального значения при г = 0, а при г = ю имеем и0 = 1/е. Таким образом, величина ю характеризует размеры пучка в поперечном направлении; ее называют размером пятна (при данной координате г). Отметим, что поскольку интенсивность излучения определяется величиной I ссЕ2, то получаем выражение I = /тахехр ~[2(х2 + у2)/ю2]. Если определить размер пятна профиля интенсивности ю1 как величину I = /тах/е, то получим, что ' юг = и>/у/2. Обычно, когда говорят о размере пятна, то чаще имеют в виду размер пятна профиля напряженности электрического поля ю, чем размер пятна профиля интенсивности.
Отметим, что на расстоянии от оси пучка, равном одному размеру пятна профиля напряженности поля, интенсивность / уменьшается в 1/е2раз по сравнению с ее величиной в максимуме.
Для того чтобы выяснить смысл входящего в формулу (4.7.8) параметра Л» обратимся к фазовому множителю в соотношении (4.7.9). Сравнение с соотношением (4.7.7), которое относится к сферической волне, показывает, что эти два выражения идентичны. Это позволяет отождествить Л в формуле (4.7.8) с радиусом кривизны волнового фронта гауссова пучка. Для того чтобы увй" деть это еще более отчетливо, рассмотрим поверхность равных фаз в гауссовом пучке, пересекающую ось г в данной точке г'. Тогда координаты х, у, г точек
На этой поверхности должны удовлетворять равенству кг + к(х2 + у2)/211 = кг что дает:
|
Х2 л-у2 |
Г = г'
|
2R |
(4.7.10)
Таким образом, соотношение (4.7.10) показывает, что поверхность равных фаз является параболоидом вращения вокруг оси г. Далее, можно показать, что радиус кривизны этого параболоида в точке х = у = 0, т. е. на оси пучка, просто равен R. Это достаточно ясно объясняет, почему в приближении параксиальных волн фазовые множители сферической волны, (4.7.7), и гауссова пучка, (4.7.9), одинаковы.
