КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И УСИЛЕНИЯ
Рассмотрим вначале два энергетических состояния в зоне проводимости и валентной зоне с энергиями соответственно Е2 и Е{, разность которых равна Е = hv09 где v0 — частота перехода. При выполнении правил отбора по к, задаваемых соотношением (3.2.22), для заданной частоты v0 энергии Е2 и Е[ определены однозначно. Действительно, используя (3.2.3) и (3.2.2), можно записать:
Е2 = Eg + (h2k2 /2 mc), (3.2.26а)
E{=-n2k2/2mv, (3.2.266)
Полагая k = kc = kv. Поскольку E2 - E[ = E0 = hv0, то из (3.2.26) получаем:
Hv о = Eg + (h2k2/2mX (3.2.26b)
Где mr — приведенная эффективная масса для полупроводника, определяемая соотношением m~1 =пг~1 --rn~1. Соотношения (3.2.26) представляют собой набор трех уравнений с тремя неизвестными Е2, Ег и k.
На следующем этапе введем объединенную плотность состояний (англ. joint density of states) в шкале разностей энергий Е0 = Е2 - Е[ таким образом, что р$Е0 будет определять плотность числа переходов с энергиями, лежащими в интервале от Е0 до Е0 + йЕ0. При выполнении правил отбора по к и спину, задаваемых соотношениями (3.2.22) и (3.2.23), любое состояние с данным спином, например в валентной зоне, связано переходом только с одним состоянием в зоне проводимости, обладающим тем же самым спином. Следовательно, число переходов равно числу соответствующих состояний в валентной зоне или зоне проводимости. Таким образом, запишем р^Е0 = р(&)^й, где р(к) = рс>и(к) определяется выражением (3.2.7), и в результате получим:
РД£0) = (к2/п2)(йк/йЕ0). (3.2.27)
Используя (3.2.26в), преобразуем соотношение (3.2.27) к
М£о) = ^Г {Щг]'ео-Е^2. (3.2.28)
Введем также объединенную плотность состояний рДу0) в шкале частот переходов у0 = Е0/к. Поскольку рДу0)<2у0 = р^(Е0)йЕ0, то из (3.2.28) получаем:
РДуо) = ||(2тг)3'2[Ну0 - Ее?'2. (3.2.29)
Рассмотрим теперь элементарное число переходов в единице объема йИ = рДу0)с2у0, частоты которых лежат в интервале между у0иу0 + с1. Если происходит поглощение, то нижнее состояние с энергией Е[ должно быть занято электроном, тогда как верхнее состояние с энергией Е2 одновременно должно быть свободным. Таким образом, число переходов, на которых может произойти поглощение, равно:
<та =№ШЕ[)[1-аЕ'2)ъ (3.2.30)
Где Ъ{Е[)— вероятность заселения нижнего состояния, а [1-&(Е2)]— вероятность того, что верхнее состояние свободно. Отметим, что здесь рассматривается общий случай теплового равновесия внутри каждой из зон, так что Ъ(Е{)я^(Е2) определяются соотношениями (3.2.116) и (3.2.11а), в которых Е^иЕс следует заменить соответственно на Е{лЕ2. Для того чтобы рассчитать общее, результирующее поглощение, необходимо учесть также переходы с вынужденным излучением между теми же самыми состояниями. Они будут происходить, когда верхнее состояние занято электроном, а нижнее одновременно является свободным. Таким образом, число переходов, на которых может произойти вынужденное излучение, будет равно:
(3.2.31)
После того как элементарные числа возможных переходов с поглощением и вынужденным излучением определены, можно, используя (2.4.32), записать вклад в коэффициент поглощения на частоте V в виде йа = ст(у — у0)(с^А1а -
- йЫ8е)у где с = стл — поперечное сечение при однородном уширении для перехода Е[ -> Е2 Таким образом, из (3.2.24) получаем:
Йа={^^^-ё(у-у0)Р1(уЖ(Е1)-иЕ'2№0. (3.2.32)
<Т1Е(^Сг1 J о
Полный коэффициент поглощения на частоте V определяется из (3.2.32) путем интегрирования по всем частотам переходов у0. Если предположить, что контур #(у - у0) как функция у0 гораздо уже, чем функции ру(у0) и (/с - /„), то ё(у - у0) можно аппроксимировать 8-функцией, 8 = 8(у - у0). В этом случае получим:
(з-2-зз)
Где Е2 и Е[ — это энергии двух состояний, отличающиеся на величину к. Они могут быть легко определены из соотношений (3.2.26) путем замены к на Ну.
В соответствии с соотношением (3.2.33) коэффициент поглощения а = а(у) можно представить в виде:
А = оцШ£5)-£(**)]. (3.2.34)
^ _Г2тг2у>2 (л
А° уп£0скJ 3 Р;(у)‘ (3.2.35)
Смысл величины а0 = ос0(у) становится понятен, если рассмотреть полупроводник при полном тепловом равновесии при Т = О К. Квазиуровни Ферми совпадают в этом случае с уровнем Ферми, и если этот уровень находится внутри запрещенной зоны, то получаем (Е{) = 1 и /с(Е2) = 0. Тогда а(у) = а0(у), что является максимальным коэффициентом поглощения, которым может обладать полупроводник на частоте V. Отметим, что в беспримесных полупроводниках и при условии Её^> кТ, что справедливо для всех соединений групп Ш-1У, по-прежнему имеем (Е{) = 1 и (Е2) = 0, т. е. а = а0 даже при комнатной температуре. Из соотношения (3.2.35), используя (3.2.29), в котором проведена замена у0 на V, получаем:
А = а0 =_^1-^-(2тг)3/2[/гу-£г]1/2. (3.2.36)
Следовательно, частотная зависимость а0(у) с хорошей точностью определяется только частотной зависимостью множителя (к — Её)х/2.
В (3.2.36) дает а0 = 19,760[Ду - Её]1/2, где а0 выражается в см-1, а энергия — в эВ. Коэффициент поглощения, расчитанный с использованием последнего выражения, изображен на рис. 3.16 в зависимости от (Е - Её)у где Е — Ну. Отметим, что когда Ну начинает превышать ширину запрещенной зоны всего на 10 мэВ, коэффициент поглощения достигает уже очень большой величины ( » 2000 см-1).
|
|
|
(Е~Ее) [мэВ] |
|
Рис. 3.16 Идеализированная зависимость коэффициента поглощения а от разности энергии фотона Е и ширины запрещенной зоны Е8 для беспримесного объемного полупроводника ОаАв |
Определим далее коэффициент усиления в полупроводнике с инверсной заполненностью (заселенностью) состояний. Сразу можно заметить, что предшествующее рассмотрение остается справедливым, если переставить индек - сы и и с. Таким образом, из (3.2.34) видно, что коэффициент усиления опре - ) деляется выражением:
8 = о. оШЕй-МКЪ (3.2.37) |
Отсюда следует, что для любой частоты перехода максимальная величина коэффициента усиления достигается при Т = 0 К и равна а0. Отметим, исходя из (3.2.37), что при любой температуре условием усиления является ; выполнение неравенства ^(Е2)> ^(Е[). С помощью соотношений (3.2.11а, б) можно показать, что это неравенство эквивалентно условию
ЕЬ-Е{<Е'Рс-Е'Ри. (3.2.38) ]
Это необходимое условие получения общего усиления было впервые получено Бернаром и Дюраффуром [6]. Видно, что множитель Ъ(Е2) - ^(Е{) в (3.2.37) возникает из выражения Ь(Е2)[1-^(Е{)[1-Ъ(Е2)]9 которое определяет разность вероятностей вынужденного излучения и поглощения. Таким образом, условие Бернара-Дюраффура означает, что число актов вынужденного излучения должно превышать число актов поглощения и, в этом смысле, оно эквивалентно условию Ы2 > ЛГ1 для простого, двухуровневого атома. Соотношение (3.2.38) можно интерпретировать графически, рассмотрев простейший случай Т = 0 К. При заданном уровне электрон-дырочной инжекции расположение квазиуровней Ферми будет таким, как показано на рис. 3.17, где заштрихованные области заполнены электронами, а незаштри - хованные области свободны от них (т. е. заполнены дырками в валентной зоне). Условие (3.2.38) в этом случае означает, что уровень энергии 2 должен находиться в заполненной области, тогда как уровень энергии 1 — в неза-^
Полненной области на рис. 3.17. Однако строгий вывод условия Берна - ра-Дюраффура показывает, что неравенство (3.2.38) в действительности выполняется при любой температуре.
 Важно вспомнить теперь, что Е2~Е[= hv, и необходимо, чтобы выполнялось условие hv > Eg. Тогда из неравенства (3.2.38) получаем соотношения:
Важно вспомнить теперь, что Е2~Е[= hv, и необходимо, чтобы выполнялось условие hv > Eg. Тогда из неравенства (3.2.38) получаем соотношения:
Eg^hv^E'Fc-E'Fv, (3.2.39)
Определяющие ширину полосы усиления в полупроводнике. В соответствии с (3.2.39), для получения усиления на любой частоте необходимо, чтобы выполнялось неравенство EfFc - Epv >Eg; предельный случай
E'fc ~EfFv = Её (3.2.40)
Называют условием прозрачности (англ. transparency condition). В этом случае получаем g = 0 при v = Eg/h. Для обеспечения этого условия необходимо создать определенную плотность числа, или концентрацию, электронов в зоне проводимости (и дырок — в валентной зоне), обозначаемую как Ntr, которую называют концентрацией при условии прозрачности, или кратко, концентрацией прозрачности (англ. transparency density).
Пример 3.7. Расчет концентрации прозрачности для СаАв. Прежде всего, удобно представить соотношение (3.2.40) в системе отсчета энергий, изображенной на рис. 3.9а. Согласно (3.2.3), имеем ЕРс =Её + ЕРс иЕРо ~-ЕРи; тогда соотношение (3.2.40) преобразуется в ЕРс +ЕРи =0. Из рис. 3.15а видно, что ЕРс/кТ зависит только от (N/N0), т. е. можно записать ЕРс /кТ =<р(И/Ис). Аналогично можно записать ЕРи /кТ =ф(А/уА^), и тогда условие прозрачности преобразуется к
Ф(ЛГ, г/ЛГс) + Ф^/ЛГ.) = 0. (3.2.41)
Для того чтобы получить Ы1Г для ОаАз из (3.2.41), построим на рис. 3.156 кривую зависимости суммы ЕРс /кТ + ЕРо /кТ от концентрации носителей N (показана пунктирной линией). Для каждого значения N эта кривая получается суммированием величин, задаваемых двумя сплошными линиями на этом рисунке. В соответствии с (3.2.41) можно утверждать, что концентрация при условии прозрачности Ntr соответствует такой концентрации носителей, при которой пунктирная линия на рис. 3.156пересекает нулевой уровень оси ординат. Из рис. 3.156 получаем, что ЛГ, г = 1,2 • 1018 см-3.
|
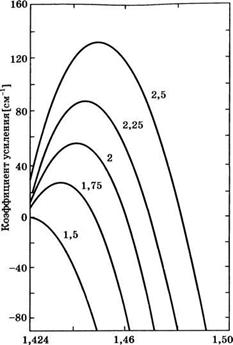
Hv [эВ] Рис. 3.18 Зависимости коэффициента усиления от энергии фотона, с концентрацией инжектированных носителей N (в единицах 1018 см-3) в качестве параметра, рассчитанные из соотношения (3.2.37) для GaAs при Т = 300 К (перепечатано из [15], с разрешения John Wiley & Sons, Inc.) |
|
Концентрация носителей [10 см ] Рис. 3.19 Зависимости максимального коэффициента усиления от концентрации носителей для GaAs (перепечатано из [15], с разрешения John Wiley & Sons, Inc.) |
![КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И УСИЛЕНИЯ подпись:
концентрация носителей [10 см ] рис. 3.19
зависимости максимального коэффициента усиления от концентрации носителей для gaas (перепечатано из [15], с разрешения john wiley & sons, inc.)](/img/655/image253.gif) Когда концентрация инжектированных электронов N превышает концентрацию прозрачности, имеем Е'Рс - Е'Ри >Её, и, согласно (3.2.39), будет происходить общее усиление фотонов с энергиями между Её и ЕРс - Е'р9. Коэффициент усиления в зависимости от энергии фотонов, рассчитанный из соотношения (3.2.37) для ОаАв, показан на рис. 3.18, где концентрация инжектированных носителей N выступает в качестве параметра. Видно, что по мере ее увеличения разность квазиэнергий Ферми, Е'Рс - Е'Ри, увеличивается, и это приводит к соответствующему увеличению ширины полосы усиления. Однако даже при самой высокой из приведенных на рис. 3.18 концентрации инжектированных носителей ширина этой полосы оказЫ" вается менее 0,07 эВ, т. е. составляет малую долю ширины запрещенной зоны. Из рис. 3.18 можно также увидеть, что максимальное значение коэффициента усиления для каждой кривой увеличивается с ростом N. Снова для ОаАв, на рис. 3.19 показана зависимость этого максимального коэффициента усиления от концентрации инжектированных электронов. Дл* | типичных коэффициентов усиления, представляющих интерес с точК#^
Когда концентрация инжектированных электронов N превышает концентрацию прозрачности, имеем Е'Рс - Е'Ри >Её, и, согласно (3.2.39), будет происходить общее усиление фотонов с энергиями между Её и ЕРс - Е'р9. Коэффициент усиления в зависимости от энергии фотонов, рассчитанный из соотношения (3.2.37) для ОаАв, показан на рис. 3.18, где концентрация инжектированных носителей N выступает в качестве параметра. Видно, что по мере ее увеличения разность квазиэнергий Ферми, Е'Рс - Е'Ри, увеличивается, и это приводит к соответствующему увеличению ширины полосы усиления. Однако даже при самой высокой из приведенных на рис. 3.18 концентрации инжектированных носителей ширина этой полосы оказЫ" вается менее 0,07 эВ, т. е. составляет малую долю ширины запрещенной зоны. Из рис. 3.18 можно также увидеть, что максимальное значение коэффициента усиления для каждой кривой увеличивается с ростом N. Снова для ОаАв, на рис. 3.19 показана зависимость этого максимального коэффициента усиления от концентрации инжектированных электронов. Дл* | типичных коэффициентов усиления, представляющих интерес с точК#^
Зрения полупроводниковых лазеров (20 < g < 80 см-1), зависимость на рис. 3.19 может быть аппроксимирована линейным соотношением, т. е. можно записать:
G = a(N~Ntr,), (3.2.42)
Где 1,5 • 10~16 см2 для GaAs. Следует отметить, что определенная таким образом величина а имеет некоторое сходство с поперечным сечением усиления, определенным для атомарных систем (ср. соотношения (3.2.42) и (2.4.35)). Однако, как уже говорилось, понятие сечения не подходит для случая дело - кализованных волновых функций, таких как у электрона в полупроводнике. По этой причине, поскольку из (3.2.42) получаем а = dg/dN, величину о часто называют дифференциальным коэффициентом усиления для полупроводника. Сохраним, тем не менее, обозначение а для этого дифференциального коэффициента усиления как напоминание о том, что величина а имеет размерность площади.
Большинство примеров, рассмотренных в данном разделе, относилось к частному случаю полупроводника GaAs. Тем не менее многие другие соединения также представляют интерес с точки зрения их использования в качестве лазерных материалов. Характерным примером является четверной твердый раствор In^Ga^As^^, который, в зависимости от параметров состава хну, перекрывает так называемые второе и третье окна прозрачности оптических волокон для линий связи (1300 нм < X < 1600 нм). Для сравнения в табл. 3.1 приведены величины Eg, тс/т0, mhh/m0, Ntr и а для In0,73Ga0,27Aso,6Po,4 = 1300 нм) и для Ino>58Gao,42Aso,9Po, i = 1550 нм) t7]’ a
Также соответствующие величины для GaAs, использованные в этом разделе. Отметим, что приведенные в табл. 3.1 величины Ntr и а попадают в диапазоны значений, встречающихся для этих полупроводников в литературе, и их следует рассматривать только как ориентировочные. Однако представляется несомненным, что как Ntr, так и а в InGaAsP меньше соответствующих величин в GaAs.
Таблица 3.1
Значения длины волны испускания X, ширины запрещенной зоны Eg, эффективной массы электронов в зоне проводимости ТПс, эффективной массы тяжелых дырок mhh, концентрации носителей при условии прозрачности Ntr, дифференциального коэффициента усиления ст и времени жизни х в объемных полупроводниках GaAs (X = 850 нм) и InGaAsP (к = 1300 нм и X = 1500 нм)
|
GaAs |
IlM,73Gao,27Aso,6Po,4 |
Ino,68Gao,42Aso, ePo, i |
|
|
X [нм] |
840 |
1310 |
1550 |
|
Ев [эВ] |
1,424 |
0,96 |
0,81 |
|
ГПс/то |
0,067 |
0,058 |
0,046 |
|
NihfJmo |
0,46 |
0,467 |
0,44 |
|
Ntr [10-18 см 3] |
1,2 |
1 |
1 |
|
А [10~16 см2] |
1,5 |
1,2^-2,5 |
1,2^-2,5 |
|
Х [не] |
3 |
4,5 |
4,5 |
|
Где А21 — вероятность спонтанного излучен! Ления ё пропорционален /с(Е2 ) - (2^ ). |