Процессы и аппараты упаковочного производства
Теплопередача при нестационарном режиме
Нестационарный перенос теплоты, который происходит в теплообменных аппаратах непрерывного действия при их пуске, остановке или изменении режима их работы, обычно в тепловых расчетах не учитывают, поскольку такие периоды работы непрерывно действующих теплообменников кратковременны. Вместе с тем в аппаратах периодического действия (например, в регенеративных теплообменниках, аппаратах с рубашкой и др.) нестационарный перенос теплоты является основным, и расчет такого процесса нагревания или охлаждения через стенку имеет важное практическое значение
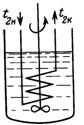
Рис. 11-19. К выводу уравнений нестационарной теплопередачи
Примем, например, что горячая жидкость в количестве G1 Должна быть охлаждена водой в аппарате с мешалкой (рис. 11-19). Заданными величинами являются также начальная T1Н И конечная T1К Температуры охлаждаемой жидкости, начальная температура T2н охлаждающей жидкости, поверхность теплопередачи F. Полагаем, что коэффициент теплопередачи К В течение процесса практически постоянен, плотности жидкостей в интервале изменения рабочих температур и давлений остаются постоянными, в аппарате вследствие интенсивно работающей мешалки создается режим идеального смешения (МИС). Поэтому температура T1 =f( ![]() ), но всех точках жидкости одинакова в каждый момент времени
), но всех точках жидкости одинакова в каждый момент времени ![]() .
.
В некоторый произвольный момент времени ![]() , когда температура охлаждаемой жидкости равна T1 Разность температур теплоносителей (движущие силы теплопередачи) на входе воды составляет
, когда температура охлаждаемой жидкости равна T1 Разность температур теплоносителей (движущие силы теплопередачи) на входе воды составляет ![]() , а на выходе
, а на выходе ![]() = T1- T2K. Поскольку температуры T1 И T2к изменяются во времени, то изменяется во времени и средняя разность температур. Поэтому
= T1- T2K. Поскольку температуры T1 И T2к изменяются во времени, то изменяется во времени и средняя разность температур. Поэтому
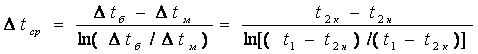 (11.83)
(11.83)
Выражение (11.83), строго говоря, справедливо при условии пренебрежения скоростью изменения энтальпии теплоносителя внутри змеевика по сравнению со скоростью изменения энтальпии теплоносителя в объеме аппарата. Подставим выражение (11.83) и уравнение теплопередачи
![]() (11.84)
(11.84)
По уравнению теплового баланса величину dQ можно выразить так:
DQ=G2c2(t2k - t 2H)d ![]() (11.85)
(11.85)
Из сопоставления уравнений (11.84) и (11.85) следует :
![]() , (11.86)
, (11.86)
Или
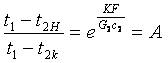
(11.87)
Для второго теплоносителя
![]()
При противотоке таким же образом получаем
![]() (11.106)
(11.106)
Для первого теплоносителя
![]()
Выражения (11.104)-(11.106) позволяют провести сравнение эффективности прямотока и противотока при одинаковых условиях.
Для прямотока
![]()
Для противотока
![]()
Отношение этих величин
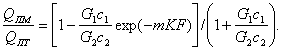 (11.107)
(11.107)
Поскольку
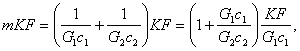
Можно записать
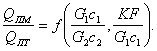 (11.108)
(11.108)
Оба аргумента изменяются в пределах от 0 до ![]() .
.
Результаты численных расчетов отношения QПМ/QПТ Приведены на рис.11-21, из которого видно, что рассматриваемые схемы равноценны в двух случаях: 1) массовая теплоемкость (Gc) Одного из теплоносителей намного превышает массовую теплоемкость второго; 2) отношение KF/G1C1 Близко к нулю.
В первом случае температура теплоносителя с большой массовой теплоемкостью изменяется слабо, во втором изменение температуры теплоносителей мало по сравнению с ![]() Tcp. Во всех остальных случаях при противотоке при прочих равных условиях поверхность теплопередачи оказывается меньшей, чем при прямотоке.
Tcp. Во всех остальных случаях при противотоке при прочих равных условиях поверхность теплопередачи оказывается меньшей, чем при прямотоке.
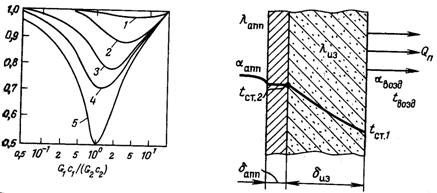
Рис. 11-21. Сравнение прямотока и противотока:
1 – KF/(G1C1)=0,1; 2 – 0,5; 3 – 1,0; 4 – 2,0; 5 - ![]()
Рис. 11-22. К определению толщины стенки тепловой изоляции