Процессы и аппараты упаковочного производства
Уравнение теплопроводности плоской стенки
Дифференциальное уравнение теплопроводности в неподвижной среде, или уравнение Фурье:
![]() /
/ ![]() =
= ![]() .
.
При установившемся процессе ![]() /
/ ![]() =0 уравнение Фурье примет вид
=0 уравнение Фурье примет вид
![]() = 0. (11.7)
= 0. (11.7)
Поскольку коэффициент температуропроводности А = ![]() /(ср) Не может быть равен нулю, то, следоватедьно,
/(ср) Не может быть равен нулю, то, следоватедьно,
![]() = 0. (11.8)
= 0. (11.8)
Дифференциальное уравнение теплопРоводности в неподвижной среде при установившемся тепловом Режиме. Это уравнение в общем виде описывает распределение температур при переносе теплоты теплопроводностью в неподвижной среде.
Рис. 11.1. Перенос теплоты теплопроводностью при установившемся процессе через плоскую стенку
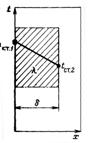
Рассмотрим перенос рис. 11.1, длина и ширина стенки существенно больше ее толщины. Примем, что tст.1 >TСт.2, Изотермические плоские поверхности параллельны оси х, коэффициент теплопроводности в интервале tст.1 - tст.2 не зависит от температуры, изменение температуры происходит только в направлении оси Х. При установившемся процессе количества теплоты (подведенное к стенке и отведенное от нее) не изменяются во времени и равны между собой.
Поскольку температурное поле одномерно, то Dt/Dy=0, ![]() T/Dz = 0, и уравнение (11.8) примет вид
T/Dz = 0, и уравнение (11.8) примет вид
![]() = 0. (11.9)
= 0. (11.9)
Интегрируем уравнение (11.9), предварительно заменив частную производную на обыкновенную:
Dt/Dx =С1; (11.10)
T=C1 Х + C2, (11.1I)
Где С1 И С2 -константы интегрирования.
Уравнение (11.11) показывает, что температура по толщине стенки изменяется прямолинейно. Для определения значений С1 и С2 Примем граничные условия: при Х = 0 T = TСт. г И TСт.1 = С2; при х = ![]() T = TСт.,2 И TСт.,2 = С1
T = TСт.,2 И TСт.,2 = С1 ![]() + С2 [из уравнения (11.11)] '
+ С2 [из уравнения (11.11)] '
Тогда TСт.,2 = С1 ![]() + TСт.1 , откуда С1 = (TCT.2 – TСт.1)/
+ TСт.1 , откуда С1 = (TCT.2 – TСт.1)/ ![]() .
.
С учетом (11.10)
![]()
Подставив полученное выражение в уравнения (11.6) и (11.6а)
имеем
Q = ![]() (tст.1 – tст.2)F
(tст.1 – tст.2)F ![]() (11.12)
(11.12)
Q=Q/(F ![]() )=
)= ![]() (tст.1 – tст.2)/
(tст.1 – tст.2)/ ![]() =
= ![]() (11.12a)
(11.12a)
Уравнение (11.12) называют Уравнением теплопроводности плоскОй стенки при установившемся процессе теплопереноса. В этом уравнении величина ![]() характеризует тепловую проводимость стенки, а обратная величина (
характеризует тепловую проводимость стенки, а обратная величина ( ![]() ) - Термическое сопротивление стенки.
) - Термическое сопротивление стенки.
Для многослойной стенки, имеющей П Слоев с разными коэффициентами теплопроводности и толщиной, к каждому слою можно применить уравнение (11.12а). Тогда
Q= ![]()
Поскольку ![]() , а
, а ![]() (причем
(причем ![]() -общая разность температур многослойной стенки;
-общая разность температур многослойной стенки; ![]() -разность температур в i-м слое), имеем
-разность температур в i-м слое), имеем
![]()
Отсюда
![]()
Или ![]()
Из выражения (11.13) следует, что для многослойной стенки общее термическое сопротивление равно сумме термических сопротивлений отдельных слоев.